PROPERTIES OF A SYSTEM
Any characteristic of a system is called a property. Some familiar properties are pressure P, temperature T, volume V, and mass m. The list can be extended to include less familiar ones such as viscosity, thermal conductivity, modulus of elasticity, thermal expansion coefficient, electric resistivity, and even velocity and elevation.
Not all properties are independent, however. Some are defined in terms of other ones. For example, density is defined as mass per unit volume.
The density of a substance, in general, depends on temperature and pressure. The density of most gases is proportional to pressure, and inversely proportional to temperature. Liquids and solids, on the other hand, are essentially in- compressible substances, and the variation of their density with pressure is usually negligible. At 20°C, for example, the density of water changes from 998 kg/m3 at 1 atm to 1003 kg/m3 at 100 atm, a change of just 0.5 percent. The density of liquids and solids depends more strongly on temperature than they do on pressure. At 1 atm, for example, the density of water changes from 998 kg/m3 at 20°C to 975 kg/m3 at 75°C, a change of 2.3 percent, which can still be neglected in most cases.
Sometimes the density of a substance is given relative to the density of a well-known substance. Then it is called specific gravity, or relative density, and is defined as the ratio of the density of a substance to the density of some standard substance at a specified temperature (usually water at 4°C, for which rH O = 1000 kg/m3). That is,
Note that the specific gravity of a substance is a dimensionless quantity. However, in SI units, the numerical value of the specific gravity of a substance will be exactly equal to its density in g/cm3 or kg/L (or 0.001 times the density in kg/m3) since the density of water at 4˚C is 1 g/cm3 = 1 kg/L = 1000 kg/m3. For example, the specific gravity of mercury at 0°C is 13.6. Therefore, its density at 0°C is 13.6 g/cm3 = 13.6 kg/L = 13,600 kg/m3. The specific gravities of some substances at 0°C are 1.0 for water, 0.92 for ice, 2.3 for concrete, 0.3–0.9 for most woods, 1.7–2.0 for bones, 1.05 for blood, 1.025 for seawater, 19.2 for gold, 0.79 for ethyl alcohol, and about 0.7 for gasoline. Note that substances with specific gravities less than 1 are lighter than water, and thus they will float on water.
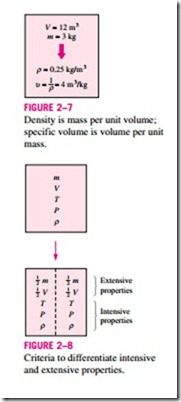
A more frequently used property in thermodynamics is the specific volume. It is the reciprocal of density (Fig. 2–7) and is defined as the volume per unit mass:
Properties are considered to be either intensive or extensive. Intensive properties are those that are independent of the size of a system, such as temperature, pressure, and density. Extensive properties are those whose values depend on the size—or extent—of the system. Mass m, volume V, and total energy E are some examples of extensive properties. An easy way to deter- mine whether a property is intensive or extensive is to divide the system into two equal parts with a partition, as shown in Fig. 2–8. Each part will have the same value of intensive properties as the original system, but half the value of the extensive properties.
Generally, uppercase letters are used to denote extensive properties (with mass m being a major exception), and lowercase letters are used for intensive properties (with pressure P and temperature T being the obvious exceptions). Extensive properties per unit mass are called specific properties. Some ex- amples of specific properties are specific volume (v = V/m) and specific total energy (e = E/m).
Matter is made up of atoms that are widely spaced in the gas phase. Yet it is very convenient to disregard the atomic nature of a substance, and view it as a continuous, homogeneous matter with no holes, that is, a continuum. The continuum idealization allows us to treat properties as point functions, and to assume the properties to vary continually in space with no jump discontinuities. This idealization is valid as long as the size of the system we deal with is large relative to the space between the molecules. This is the case in practically all problems, except some specialized ones.
To have a sense of the distance involved at the molecular level, consider a container filled with oxygen at atmospheric conditions. The diameter of the oxygen molecule is about 3 X 10-10 m and its mass is 5.3 X 10-26 kg. Also, the mean free path of oxygen at 1 atm pressure and 20°C is 6.3 X 10-8 m. That is, an oxygen molecule travels, on average, a distance of 6.3 X 10-8 m (about 200 times of its diameter) before it collides with another molecule. Also, there are about 3 X 1016 molecules of oxygen in the tiny volume of 1 mm3 at 1 atm pressure and 20°C (Fig. 2–9). The continuum model is applicable as long as the characteristic length of the system (such as its di- ameter) is much larger than the mean free path of the molecules. At very high vacuums or very high elevations, the mean free path may become large (for example, it is about 0.1 m for atmospheric air at an elevation of 100 km). For such cases the rarefied gas flow theory should be used, and the impact of individual molecules should be considered. In this text we will limit our con- sideration to substances that can be modeled as a continuum.