PROPERTIES OF AIR AND GASES
Clean, dry air is a mechanical mixture of approximately 78% by volume of nitrogen and 21% oxygen, the remaining 1% being made up of minor quantities of other gases (see Table 1). The composition of air remains substantially the same between sea level and an altitude of about 20 kilometres, but its density decreases with increasing altitude, and varies with pressure and temperature. At sea level, at a pressure of 1bar and a temperature
of 150C, the density of air is 1.209 kg/m3 Thus 1 kg of air has a volume of 0.827 m3
At a specific temperature and pressure, the number of molecules in a unit volume is constant for any gas or mixture of gases. For a temperature of O”C and a pressure of one atmosphere, this number is 2.705 x 1019 molecules per cubic centimetre.
At standard temperature and pressure, the mean velocity of gas molecules is of the order of 500 rn/s with a mean free path between intermolecular collision, for air, of the order of 3 x 1Q-16 millimetres. The rate of collision under such conditions is responsible for the pressure exerted by the air (or any gas) on a surface immersed in it, or on walls containing the gas. The pressure therefore of any gas depends on its mass density, the number of molecules present and their mean velocity.
The effect of a change in temperature is to modify the value of the mean velocity. Hence in the absence of any other change, the resultant pressure will vary with the temperature. Similarly. any change in volume will effectively modify the mass present and again affect
the pressure. Thus pressure, temperature and volume are interrelated. This relationship can be expressed in the following form for a perfect gas (which assumes that the molecules are perfectly elastic, are negligible in size compared with the length of the mean free path and exert no force on each other):
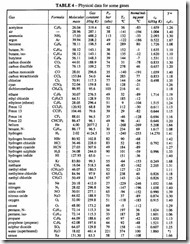
The value of R in SI units is 8314 J/(K kmol), which for air is equivalent to 287 J/(kg K). For other gases see Table 4.
Atmospheric air
Atmospheric air normally contains water vapour, and the total pressure of the air is the sum of the partial pressures of the dry air and the water vapour(follows from Dalton’s Law of Partial Pressures). The air is saturated when the partial pressure of the water vapour is equal to the saturation pressure of the water vapour at that temperature. The saturation pressure is dependent only upon the temperature (see also Table 2 and Figure 1).
When air is cooled at constant pressure, the dew point is reached when the partial pressure is equal to the saturation pressure. Any further cooling will then result in water separating by condensation (see also Table 3).
Water content of moist air
The water vapour content of moist air can be determined from the following equations derived from the gas law:
Condensation of water in compressed air
A common problem in compressed air is the calculation of the amount of water which condenses out when a compressor takes in air at one temperature and pressure and delivers it at another. A further equation, which derives from the above, may be used.
The mass of water which can be held in air at a temperature of T2 K and a pressure of P2 bar per 1000 litres (1m3) at a temperature ofT2 Kanda pressure ofP1 bar is given by
Therefore the mass of water condensed out per 1000 litre= 10.264- 3.962 = 6.302 g. The condensation rate for a compressor of 1000 lis is 6.302 gls.
Effects of compressibility
The properties of real gases differ from those of the ideal gas whose behaviour follows exactly the gas equation PV = wRT.
For most practical purposes this equation is adequate for engineering calculations. It is sometimes necessary to take into account the effect of compressibility near to the liquid state of the gas. This is conveniently done by replacing the gas equation by PV = ZwRT.
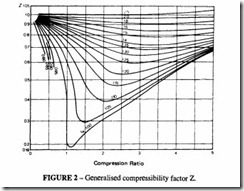
In this expression, Z is known as the compressibility factor; it is the ratio of the actual volume of the gas to its value calculated in accordance with the ideal gas law.
Compressibility charts are available for a number of gases. These are derived experi mentally and should be used if available. Alternatively a generalised chart can be used; such a chart is based on the fact that most gases behave in the same way when close to their
critical temperature and pressure. Figure 2 shows such a chart. Another way of expressing this is by saying that nearly all gases behave the same when their reduced pressures and reduced temperatures are equal. The reduced pressure is the ratio of the actual pressure to the critical pressure and similarly the reduced temperature is the ratio of the actual temperature to the critical temperature.
When dealing with a pure gas the procedure is as follows:
a) Look up the critical pressure, Per. and critical temperature Tcr, from Table 4.
b) Calculate PR =PIPcr and TR = Tffcr. where P and Tare the actual working pressure and temperature.
c) Read off the value of Z from Figure 2 .
When dealing with a mixture of gases such as natural gas, it is necessary first to calculate thepseudo-critical temperature and thepseudo-critical pressure of the mixture.lf there are m gases in the mixture:
where PRM and TRM are thepseudo-critical pressure and pseudo-critical temperature of the mixture
an is the proportion of the nth component in the mixture
PRN is the reduced pressure of the nth component
TRN is the reduced temperature of the nth component
The value of Z is found from Figure 2 as before.
The factor Z can then be used to modify the gas equation as above.
The velocity and attenuation of sound in air
For any gas at moderate pressure, the velocity of sound is given by:
where m is the molecular weight. Thus to a first order, c is proportional to +T and is independent of the pressure. At low frequencies, the velocity of sound Co, at 20°C in dry air is 331 rn/s. The effect of water vapour on the velocity of sound is complex; as water is added to dry air the velocity at first decreases so that at 14% relative humidity, it is 0.995c0; above 30% relative humidity, the velocity increases linearly with increasing moisture content such that at 100% relative humidity it is 1.003co.
The attenuation of sound in air varies with temperature, water vapour content and frequency. It is usually expressed in dB/km. Table 5 gives some typical values for the variation in attenuation with frequency and humidity at 20°C and a pressure of 1 atmosphere.
Incoming search terms:
- basic characteristics of pneumatic gases
- peoperties of ari in pneumatics
- properties of air in pneumatics
- propreties of pneumatic gases