Fundamental Principles
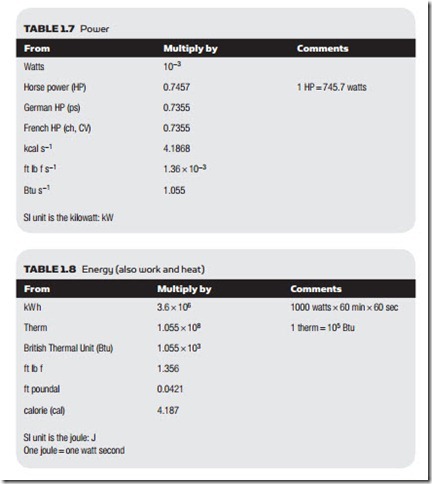
The SI unit of power is the watt, defined as 1 J s−1. This is by far the most common unit of power, as kW is almost universally used for the measurement of electrical power.
The Imperial system uses horse power (HP) which was used historically to define motor powers. One horse power is defined as 550 ft lb f s−1. Table 1.7 compares units of power.
A British Thermal Unit (Btu) is the energy required to raise the temperature of one pound of water by one degree Fahrenheit.
A calorie is the energy required to raise the temperature of one gram of water by one degree Centigrade.
A kilocalorie (often called a Calorie on food packaging) is 103 calories.
Work can be considered as the time integral of power (often described loosely as total power used). As electrical power is measured in watts or kilowatts (1 kW = 103 W), the kilowatt hour (kW h) is another representation of work or energy.
torque
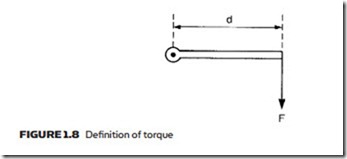
The term torque is used to define a rotary force, and is simply the product of the force and the effective radius as shown in Figure 1.8. We thus have:
T = F × d (1.7)
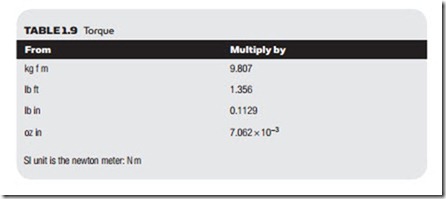
In the Imperial system the unit is lb ft, in metric systems the unit is kg f m or kg f cm, and in SI the unit is N m.
Pascal’s laW
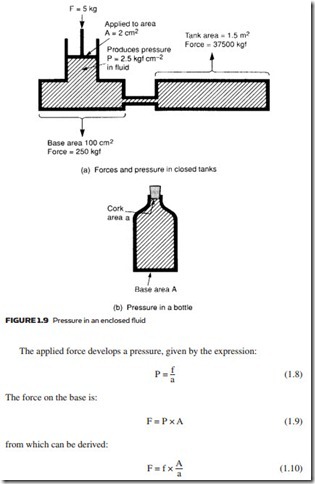
Pressure in an enclosed fluid can be considered uniform throughout a practical system. There may be small differences arising from head pressures at differ- ent heights, but these will generally be negligible compared with the system operating pressure. This equality of pressure is known as Pascal’s law, and is il- lustrated in Figure 1.9 where a force of 5 kg f is applied to a piston of area 2 cm2. This produces a pressure of 2.5 kg f cm−2 at every point within the fluid, which acts with equal force per unit area on the walls of the system.
Suppose the base of the left hand tank is 0.1 × 0.1 m to give a total area of 100 cm2. The total force acting on the base will be 250 kg f. If the top of the right hand tank is 1 m × 1.5 m, a surprisingly large upwards force of 37,500 kg f is developed. Note, the size of the connecting pipe has no effect. This principle explains why it is possible to shear the bottom off a bottle by applying a small force to the cork, as illustrated in Figure 1.9b.
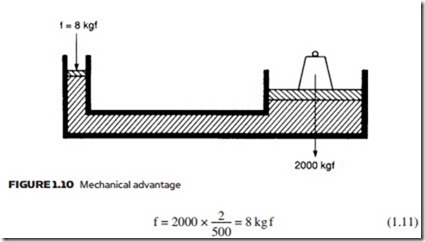
Expression 1.10 shows an enclosed fluid may be used to magnify a force. In Figure 1.10 a load of 2000 kg is sitting on a piston of area 500 cm2 (about 12 cm radius). The smaller piston has an area of 2 cm2. An applied force f given by:
will cause the 2000 kg load to rise. There is said to be a mechanical advantage of 250.
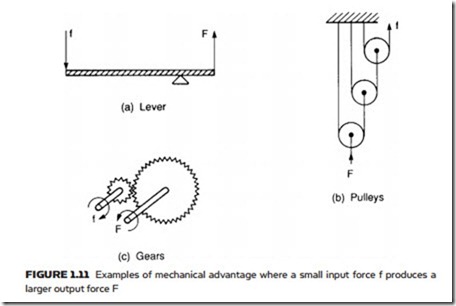
Energy must, however, be conserved. To illustrate this, suppose the left hand piston moves down by 100 cm (one meter). Because we have assumed the fluid is incompressible, a volume of liquid 200 cm2 is transferred from the left hand cylinder to the right hand cylinder, causing the load to rise by just 0.4 cm. So, although we have a force magnification of 250, we have a movement reduc- tion of the same factor. Because work is given by the product of force and the distance moved, the force is magnified and the distance moved reduced by the same factor, giving conservation of energy. The action of Figure 1.10 is thus similar to the mechanical systems of Figure 1.11, which also exhibit mechanical advantage.
Fundamental Principles
The principle of Figure 1.10 is widely used where a large force is required with small movement. Typical examples are clamps, presses, hydraulic jacks and motor car brake and clutch operating mechanisms.
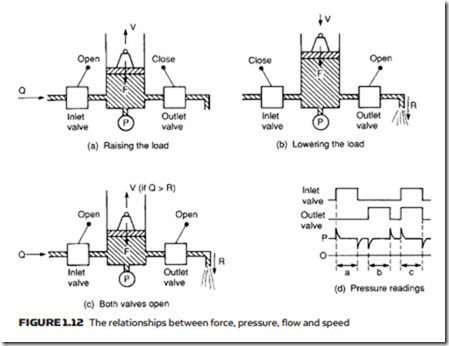
It should be noted that pressure in, say, a cylinder is determined solely by load and piston area in the steady state, and is not dependent on velocity of the piston once a constant speed has been achieved. Relationships between force, pressure, flow and speed are illustrated in Figure 1.12.
In Figure 1.12a, fluid is delivered to a cylinder at a rate of Q cm3 s−1. When the inlet valve is first opened, a pressure spike is observed as the load acceler- ates, but the pressure then settles back to a steady value of P = F/A kg f cm−2, where A is the area of the piston in cm2 and F is measured in kg f. The load rises with a velocity V = Q/A cm s−1 and velocity can obviously be controlled by adjusting flow rate Q.
In Figure 1.12b, the inlet valve has been closed, and the outlet valve opened allowing R cm−3 s−1 to flow out of the cylinder. There is again a pressure spike (negative this time) as the load accelerates downwards, but the pressure reverts to P = F/A once the steady speed V = R/A cm s−1 is achieved.
Finally, in Figure 1.12c both valves are open. The net flow is (Q − R) giving a cylinder velocity (Q − R)/A, which can be positive (rising) or negative (falling) dependent on which flow is the largest. The steady state pressure, however, is unchanged at P = F/A.