Fundamental Principles:definition of terms

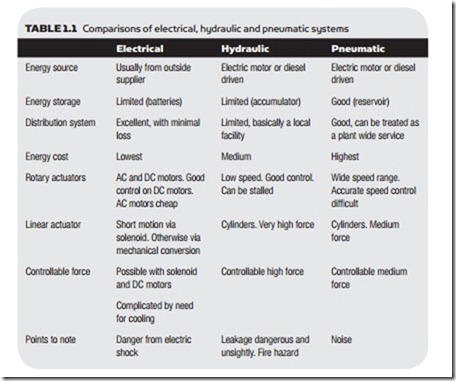
definition of terms

There is an almost universal lack of standardization of units used for measurement in industry, and every engineer will tell tales of gauges indicating, say, velocity in furlongs per fortnight. Hydraulics and pneumatic systems suffer par- ticularly from this characteristic, and it is by no means unusual to find pressure indicated at different locations in the same system in bar, kpascal and psi.

There is, however, a welcome (and overdue) movement to standardization on the International System (SI) of units, but it will be some time before this is complete. The engineer will therefore encounter many odd-ball systems in the years to come.

Any measurement system requires definition of the six units used to measure:

• length:

• mass;

• time;

• temperature;

• electrical current;

• light intensity.

Of these, hydraulic/pneumatic engineers are primarily concerned with the first three. Other units (such as velocity, force, pressure) can be defined in terms of these basic units. Velocity, for example, is defined in terms of length/time.

The old British Imperial system used units of foot, pound and second (and was consequently known as the fps system). Early metric systems used centime- ter, gram and second (known as the cgs system), and meter, kilogram and second (the mks system). The mks system evolved into the SI system which introduces a more logical method of defining force and pressure (discussed in later sections). Note that units given real persons’ names (e.g. newton) use lower case letters, but have capital letter symbols (e.g. N).

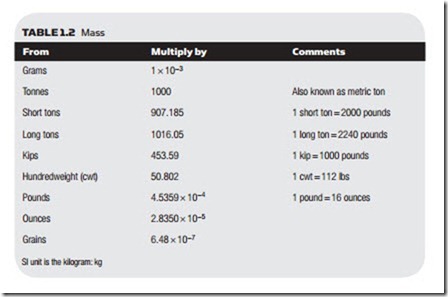
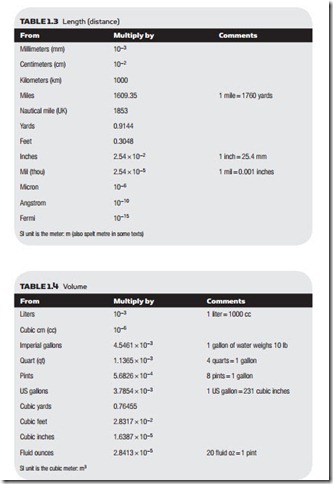
The conversion tables below convert TO the equivalent SI unit. To convert FROM SI units divide by the conversion factor. To convert between two non-SI units use a two-stage process: first multiply by the first conversion factor to con- vert to SI units then divide by the second conversion factor to give the required value in the new units. For example, in Table 1.2 to convert from kips to cwt multiply by 453.59 then divide by 50.802.

mass and force

Pneumatic and hydraulic systems generally rely on pressure in a fluid. Before we can discuss definitions of pressure, though, we must first be clear what is meant by everyday terms such as weight, mass and force.

We all are used to the idea of weight, which is a force arising from gravita- tional attraction between the mass of an object and the earth. The author weighs 75 kg on the bathroom scales; this is equivalent to saying there is 75 kg force between his feet and the ground.

Weight therefore depends on the force of gravity. On the moon, where grav- ity is about one-sixth that on earth, the author’s weight would be about 12.5 kg; in free fall the weight would be zero. In all cases, though, the author’s mass is constant.

The British Imperial fps system and the early metric systems link mass and weight (force) by defining the unit of force to be the gravitational attraction of unit mass at the surface of the earth. We thus have a mass defined in pounds and force defined in pounds force (lbs f) in the fps system, and mass in kilograms and force in kg f in the mks system.

Strictly speaking, therefore, bathroom scales which read 75 kg are measur- ing 75 kg f, not the author’s mass. On the moon they would read 12.5 kg f, and in free fall they would read zero.

If a force is applied to a mass, acceleration (or deceleration) will result as given by the well-known formula:

F = ma (1.1)

Care must be taken with units when a force F is defined in lbs f or kg f and mass is defined in lbs or kg, because resulting accelerations are in units of g, accel- eration due to gravity. A force of 25 kg f applied to the author’s mass of 75 kg produces an acceleration of 0.333 g.

The SI unit of force, the newton (N), is defined not from earth’s gravity, but directly from expression 1.1. A newton is defined as the force which produces an acceleration of 1 m s−2 when applied to a mass of 1 kg.

One kg f produces an acceleration of 1 g (9.81 m s−2) applied to a mass of 1 kg. One newton produces an acceleration of 1 m s−2 when applied to a mass of 1 kg. It therefore follows that:

1 kg f = 9.81 N

but as most instruments on industrial systems are at best 2% accurate it is rea- sonable (and much simpler) to use:

1 kg f = 10 eN

for practical applications.

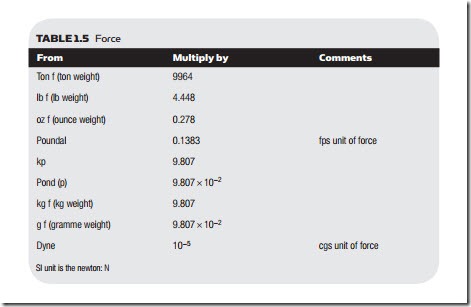
Table 1.5 gives conversions between various units of force.

A newton is the force which gives a mass of 1 kg an acceleration of one meter per second per second.

A poundal is the force which gives a mass of one pound an acceleration of one foot per second per second.

A dyne is the force which gives a mass of one gram an acceleration of one centimeter per second per second.

Weight, often confused with both force and mass, is the force that arises from the action of gravity on a mass.

Pressure

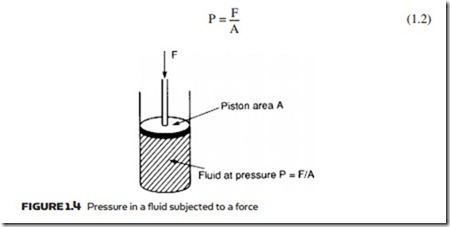
Pressure occurs in a fluid when it is subjected to a force. In Figure 1.4 a force F is applied to an enclosed fluid via a piston of area A. This results in a pressure P in the fluid. Obviously increasing the force increases the pressure in direct proportion. Less obviously, though, decreasing piston area also increases pressure. Pres- sure in the fluid can therefore be defined as the force acting per unit area, or:

Definition of Terms

Although expression 1.2 is very simple, there are many different units of pres- sure in common use. In the Imperial fps system, for example, F is given in lbs f and A is given in square inches to give pressure measured in pound force per square inch (psi).

In metric systems, F is usually given in kg f and A in square centimeters to give pressure in kilogram/force per square centimeter (kg f cm−2).

The SI system defines pressure as the force in newtons per square meter (N m−2). The SI unit of pressure is the pascal (with 1 Pa = 1 N m−2). One pascal is a very low pressure for practical use, however, so the kilopascal (1 kPa = 103 Pa) or the megapascal (1 MPa = 106 Pa) are more commonly used.

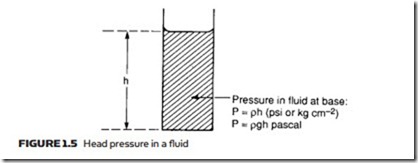
Pressure can also arise in a fluid from the weight of a fluid. This is usually known as the head pressure and depends on the height of fluid. In Figure 1.5 the pressure at the bottom of the fluid is directly proportional to height h.

In the Imperial and metric systems head pressure is given by:

where g is the acceleration due to gravity (9.81 m s−2) to give the pressure in pascal.

Pressure in a fluid can, however, be defined in terms of the equivalent head pressure. Common units are millimeters of mercury and centimeters, inches, feet or meters of water. The suffix wg (for water gauge) is often used when pres- sure is defined in terms of an equivalent head of water.

We live at the bottom of an ocean of air, and are consequently subject to a substantial pressure head from the weight of air above us. This pressure, some 15 psi, 1.05 kg fm−2, or 101 kPa, is called an atmosphere, and is sometimes used as a unit of pressure.

It will be noted that 100 kPa is, for practical purposes, one atmosphere. As this is a convenient unit for many applications 100 kPa (105 Pa or 0.1 MPa)

Fundamental Principles

has been given the name bar. Within the accuracy of instrumentation generally found in industry one bar is the same as one atmosphere.

There are three distinct ways in which pressure is measured, shown in Figure 1.6. Almost all pressure transducers or transmitters measure the pressure difference between two input ports. This is known as differential pressure, and the pressure transmitter in Figure 1.6a indicates a pressure of P1 − P2.

In Figure 1.6b the low-pressure input port is open to atmosphere, so the pressure transmitter indicates pressure above atmospheric pressure. This is known as gauge pressure, and is usually denoted by a ‘g’ suffix (e.g. psig). Gauge pressure measurement is almost universally used in hydraulic and pneumatic systems (and has been implicitly assumed in all previous discussions in this chapter).

Figure 1.6c shows the pressure transmitter measuring pressure with respect to a vacuum. This is known as absolute pressure and is of importance when the compression of gases is considered. The relationship between absolute and gauge pressure is illustrated in Figure 1.7. Pressure measurement and gas compression are discussed in later sections. Table 1.6 compares units of pressure. A typical hydraulic system operates at 150 bar, while typical pneumatic systems operate at 10 bar.