■ WHAT IS ENTROPY?
It is clear from the previous discussion that entropy is a useful property and serves as a valuable tool in the second-law analysis of engineering devices. But this does not mean that we know and understand entropy well. Because we do not. In fact, we cannot even give an adequate answer to the question, What is entropy? Not being able to describe entropy fully, however, does not take anything away from its usefulness. We could not define energy either, but it did not interfere with our understanding of energy transformations and the conservation of energy principle. Granted, entropy is not a household word like energy. But with continued use, our understanding of entropy will deepen, and our appreciation of it will grow. The next discussion will shed some light on the physical meaning of entropy by considering the microscopic nature of matter.
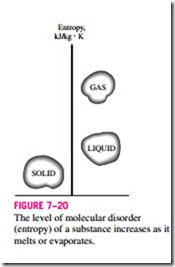
Entropy can be viewed as a measure of molecular disorder, or molecular randomness. As a system becomes more disordered, the positions of the molecules become less predictable and the entropy increases. Thus, it is not surprising that the entropy of a substance is lowest in the solid phase and highest in the gas phase (Fig. 7–20). In the solid phase, the molecules of a substance continually oscillate about their equilibrium positions, but they cannot move relative to each other, and their position at any instant can be predicted with good certainty. In the gas phase, however, the molecules move about at ran- dom, collide with each other, and change direction, making it extremely difficult to predict accurately the microscopic state of a system at any instant. Associated with this molecular chaos is a high value of entropy.
When viewed microscopically (from a statistical thermodynamics point of view), an isolated system that appears to be at a state of equilibrium may exhibit a high level of activity because of the continual motion of the molecules. To each state of macroscopic equilibrium there corresponds a large number of possible microscopic states or molecular configurations. The entropy of a system is related to the total number of possible microscopic states of that system, called thermodynamic probability p, by the Boltzmann relation, ex- pressed as
where k = 1.3806 X 10-23 J/K is the Boltzmann constant. Therefore, from a microscopic point of view, the entropy of a system increases whenever the molecular randomness or uncertainty (i.e., molecular probability) of a system increases. Thus, entropy is a measure of molecular disorder, and the molecular disorder of an isolated system increases anytime it undergoes a process. Molecules in the gas phase possess a considerable amount of kinetic energy. However, we know that no matter how large their kinetic energies are, the gas molecules will not rotate a paddle wheel inserted into the container and
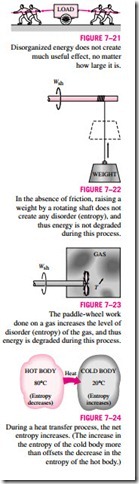
produce work. This is because the gas molecules, and the energy they possess, are disorganized. Probably the number of molecules trying to rotate the wheel in one direction at any instant is equal to the number of molecules that are trying to rotate it in the opposite direction, causing the wheel to remain motion- less. Therefore, we cannot extract any useful work directly from disorganized energy (Fig. 7–21).
Now consider a rotating shaft shown in Fig. 7–22. This time the energy of the molecules is completely organized since the molecules of the shaft are rotating in the same direction together. This organized energy can readily be used to perform useful tasks such as raising a weight or generating electricity. Being an organized form of energy, work is free of disorder or randomness and thus free of entropy. There is no entropy transfer associated with energy transfer as work. Therefore, in the absence of any friction, the process of rais- ing a weight by a rotating shaft (or a flywheel) will not produce any entropy. Any process that does not produce a net entropy is reversible, and thus the process just described can be reversed by lowering the weight. Therefore, en- ergy is not degraded during this process, and no potential to do work is lost. Instead of raising a weight, let us operate the paddle wheel in a container filled with a gas, as shown in Fig. 7–23. The paddle-wheel work in this case will be converted to the internal energy of the gas, as evidenced by a rise in gas temperature, creating a higher level of molecular disorder in the container. This process is quite different from raising a weight since the organized paddle-wheel energy is now converted to a highly disorganized form of energy, which cannot be converted back to the paddle wheel as the rotational kinetic energy. Only a portion of this energy can be converted to work by partially reorganizing it through the use of a heat engine. Therefore, energy is degraded during this process, the ability to do work is reduced, molecular disorder is produced, and associated with all this is an increase in entropy.
The quantity of energy is always preserved during an actual process (the first law), but the quality is bound to decrease (the second law). This decrease in quality is always accompanied by an increase in entropy. As an example, consider the transfer of 10 kJ of energy as heat from a hot medium to a cold one. At the end of the process, we will still have the 10 kJ of energy, but at a lower temperature and thus at a lower quality.
Heat is, in essence, a form of disorganized energy, and some disorganization (entropy) will flow with heat (Fig. 7–24). As a result, the entropy and the level of molecular disorder or randomness of the hot body will decrease with the entropy and the level of molecular disorder of the cold body will increase. The second law requires that the increase in entropy of the cold body be greater than the decrease in entropy of the hot body, and thus the net entropy of the combined system (the cold body and the hot body) increases. That is, the combined system is at a state of greater disorder at the final state. Thus we can conclude that processes can occur only in the direction of increased overall entropy or molecular disorder. That is, the entire universe is getting more and more chaotic every day.
From a statistical point of view, entropy is a measure of molecular randomness, that is, the uncertainty about the positions of molecules at any instant.
Even in the solid phase, the molecules of a substance continually oscillate, creating an uncertainty about their position. These oscillations, however, fade as the temperature is decreased, and the molecules supposedly become motionless at absolute zero. This represents a state of ultimate molecular order (and minimum energy). Therefore, the entropy of a pure crystalline substance at absolute zero temperature is zero since there is no uncertainty about the state of the molecules at that instant (Fig. 7–25). This statement is known as the third law of thermodynamics. The third law of thermodynamics pro- vides an absolute reference point for the determination of entropy. The en- tropy determined relative to this point is called absolute entropy, and it is extremely useful in the thermodynamic analysis of chemical reactions. Notice that the entropy of a substance that is not pure crystalline (such as a solid so- lution) is not zero at absolute zero temperature. This is because more than one molecular configuration exists for such substances, which introduces some uncertainty about the microscopic state of the substance.
The concept of entropy as a measure of disorganized energy can also be a plied to other areas. Iron molecules, for example, create a magnetic field around themselves. In ordinary iron, molecules are randomly aligned, and they cancel each other’s magnetic effect. When iron is treated and the molecules are realigned, however, that piece of iron turns into a piece of magnet, creating a powerful magnetic field around it.
Entropy and Entropy Generation in Daily Life
Entropy can be viewed as a measure of disorder or disorganization in a system. Likewise, entropy generation can be viewed as a measure of disorder or disorganization generated during a process. The concept of entropy is not used in daily life nearly as extensively as the concept of energy, even though entropy is readily applicable to various aspects of daily life. The extension of the entropy concept to nontechnical fields is not a novel idea. It has been the topic of several articles, and even some books. Next we present several ordinary events and show their relevance to the concept of entropy and entropy generation.
Efficient people lead low-entropy (highly organized) lives. They have a place for everything (minimum uncertainty), and it takes minimum energy for them to locate something. Inefficient people, on the other hand, are dis- organized and lead high-entropy lives. It takes them minutes (if not hours) to find something they need, and they are likely to create a bigger disorder as they are searching since they will probably conduct the search in a dis- organized manner (Fig. 7–26). People leading high-entropy lifestyles are always on the run, and never seem to catch up.
You probably noticed (with frustration) that some people seem to learn fast and remember well what they learn. We can call this type of learning organized or low-entropy learning. These people make a conscientious effort to file the new information properly by relating it to their existing knowledge base and creating a solid information network in their minds. On the other hand, people who throw the information into their minds as they study, with no effort to secure it, may think they are learning. They are bound to discover otherwise when they need to locate the information, for example, during a test. It is not easy to retrieve information from a database that is, in a sense, in the gas phase. Students who have blackouts during tests should reexamine their study habits.
A library with a good shelving and indexing system can be viewed as a low- entropy library because of the high level of organization. Likewise, a library with a poor shelving and indexing system can be viewed as a high-entropy library because of the high level of disorganization. A library with no index- ing system is like no library, since a book is of no value if it cannot be found. Consider two identical buildings, each containing one million books. In the first building, the books are piled on top of each other, whereas in the second building they are highly organized, shelved, and indexed for easy reference. There is no doubt about which building a student will prefer to go to for checking out a certain book. Yet, some may argue from the first-law point of view that these two buildings are equivalent since the mass and energy con- tent of the two buildings are identical, despite the high level of disorganization (entropy) in the first building. This example illustrates that any realistic comparisons should involve the second-law point of view.
Two textbooks that seem to be identical because both cover basically the same topics and present the same information may actually be very different depending on how they cover the topics. After all, two seemingly identical cars are not so identical if one goes only half as many miles as the other one on the same amount of fuel. Likewise, two seemingly identical books are not so identical if it takes twice as long to learn a topic from one of them as it does from the other. Thus, comparisons made on the basis of the first law only may be highly misleading.
Having a disorganized (high-entropy) army is like having no army at all. It is no coincidence that the command centers of any armed forces are among the primary targets during a war. One army that consists of 10 divisions is 10 times more powerful than 10 armies each consisting of a single division. Like- wise, one country that consists of 10 states is more powerful than 10 countries, each consisting of a single state. The United States would not be such a powerful country if there were 50 independent countries in its place instead of a single country with 50 states. The European Union has the potential to be a new economic superpower. The old cliché “divide and conquer” can be rephrased as “increase the entropy and conquer.”
We know that mechanical friction is always accompanied by entropy generation, and thus reduced performance. We can generalize this to daily life: friction in the workplace with fellow workers is bound to generate entropy, and thus adversely affect performance (Fig. 7–27). It will result in reduced productivity. Hopefully, someday we will be able to come up with some procedures to quantify entropy generated during nontechnical activities, and maybe even pinpoint its primary sources and magnitude.
We also know that unrestrained expansion (or explosion) and uncontrolled electron exchange (chemical reactions) generate entropy and are highly irreversible. Likewise, unrestrained opening of the mouth to scatter angry words is highly irreversible since this generates entropy, and it can cause consider- able damage. A person who gets up in anger is bound to sit down at a loss.
