BAROMETER AND THE ATMOSPHERIC PRESSURE
The atmospheric pressure is measured by a device called a barometer; thus, the atmospheric pressure is often referred to as the barometric pressure.
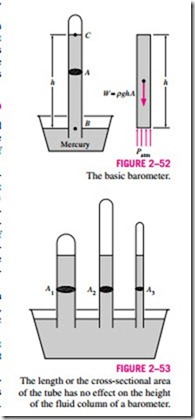
As Torricelli discovered a few centuries ago, the atmospheric pressure can be measured by inverting a mercury-filled tube into a mercury container that is open to the atmosphere, as shown in Fig. 2–52. The pressure at point B is equal to the atmospheric pressure, and the pressure at C can be taken to be zero since there is only mercury vapor above point C and the pressure it exerts is negligible. Writing a force balance in the vertical direction gives
where r is the density of mercury, g is the local gravitational acceleration, and h is the height of the mercury column above the free surface. Note that the length and the cross-sectional area of the tube have no effect on the height of the fluid column of a barometer (Fig. 2–53).
A frequently used pressure unit is the standard atmosphere, which is de- fined as the pressure produced by a column of mercury 760 mm in height at 0°C (rHg = 13,595 kg/m3) under standard gravitational acceleration (g = 9.807 m/s2). If water instead of mercury were used to measure the standard atmospheric pressure, a water column of about 10.3 m would be needed. Pressure is sometimes expressed (especially by weather forecasters) in terms of the height of the mercury column. The standard atmospheric pressure, for ex- ample, is 760 mmHg (29.92 inHg) at 0°C. The unit mmHg is also called the torr in honor of Evangelista Torricelli (1608–1647), who invented the barometer. Therefore, 1 atm = 760 torr, and 1 torr = 133.3 Pa.
The standard atmospheric pressure Patm changes from 101.325 kPa at sea level to 89.88, 79.50, 54.05, 26.5, and 5.53 kPa at altitudes of 1000, 2000, 5000, 10,000, and 20,000 meters, respectively. The standard atmospheric pressure in Denver (elevation = 1610 m), for example, is 83.4 kPa.
Remember that the atmospheric pressure at a location is simply the weight of the air above that location per unit surface area. Therefore, it changes not only with elevation but also with weather conditions.
The decline of atmospheric pressure with elevation has far-reaching ramifications in daily life. For example, cooking takes longer at high altitudes since water boils at a lower temperature at lower atmospheric pressures.
Experiencing nose bleeding is a common occurrence at high altitudes since the difference between the blood pressure and the atmospheric pressure is larger in this case, and the delicate walls of veins in the nose are often unable to withstand this extra stress.
For a given temperature, the density of air is lower at high altitudes, and thus a given volume contains less air and less oxygen. So it is no surprise that we tire more easily and experience breathing problems at high altitudes. To compensate for this effect, people living at higher altitudes develop larger lungs and thus larger chests. Similarly, a 2.0-L car engine will act like a 1.7-L car engine at 1500 m altitude (unless it is turbocharged) because of the 15 per- cent drop in pressure and thus 15 percent drop in the density of air (Fig. 2–54). A fan or compressor will displace 15 percent less air at that altitude for the same volume displacement rate. Therefore, larger cooling fans may need to be selected for operation at high altitudes to ensure the specified mass flow rate. The lower pressure and thus lower density also affects lift and drag: airplanes need a longer runway at high altitudes to develop the required lift, and they climb to very high altitudes for cruising for reduced drag and thus better fuel efficiency.