THE REVERSED CARNOT CYCLE
You will recall from the preceding chapters that the Carnot cycle is a totally reversible cycle that consists of two reversible isothermal and two isentropic processes. It has the maximum thermal efficiency for given temperature limits, and it serves as a standard against which actual power cycles can be compared. Since it is a reversible cycle, all four processes that comprise the Carnot cycle can be reversed. Reversing the cycle will also reverse the directions of any heat and work interactions. The result is a cycle that operates in the counterclockwise direction on a T-s diagram, which is called the reversed Carnot cycle. A refrigerator or heat pump that operates on the reversed Carnot cycle is called a Carnot refrigerator or a Carnot heat pump.
Consider a reversed Carnot cycle executed within the saturation dome of a refrigerant, as shown in Fig. 8–52. The refrigerant absorbs heat isothermally from a low-temperature source at TL in the amount of QL (process 1-2), is compressed isentropically to state 3 (temperature rises to TH), rejects heat isothermally to a high-temperature sink at TH in the amount of QH (process 3-4), and expands isentropically to state 1 (temperature drops to TL). The refrigerant changes from a saturated vapor state to a saturated liquid state in the condenser during process 3-4.
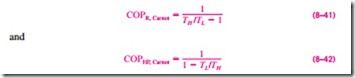
The coefficients of performance of Carnot refrigerators and heat pumps are expressed in terms of temperatures as
Notice that both COPs increase as the difference between the two temperatures decreases, that is, as TL rises or TH falls.
The reversed Carnot cycle is the most efficient refrigeration cycle operating between two specific temperature levels. Therefore, it is natural to look at it first as a prospective ideal cycle for refrigerators and heat pumps. If we could, we certainly would adapt it as the ideal cycle. As explained soon, however, the reversed Carnot cycle is not a suitable model for refrigeration cycles.
The two isothermal heat transfer processes are not difficult to achieve in practice since maintaining a constant pressure automatically fixes the temperature of a two-phase mixture at the saturation value. Therefore, processes 1-2 and 3- 4 can be approached closely in actual evaporators and condensers. However, processes 2-3 and 4-1 cannot be approximated closely in practice. This is be- cause process 2-3 involves the compression of a liquid–vapor mixture, which requires a compressor that will handle two phases, and process 4-1 involves the expansion of high-moisture-content refrigerant.
It seems as if these problems could be eliminated by executing the reversed Carnot cycle outside the saturation region. But in this case, we will have difficulty in maintaining isothermal conditions during the heat-absorption and heat-rejection processes. Therefore, we conclude that the reversed Carnot cy- cle cannot be approximated in actual devices and is not a realistic model for refrigeration cycles. However, the reversed Carnot cycle can serve as a standard against which actual refrigeration cycles are compared.