Applied Pneumatics:Flow analysis for cylinders and valves

Flow analysis for cylinders and valves

Circuit analysis

In choosing the correct sizes for circuit components, it is necessary to establish the required forces in each cylinder, the speeds of operation and the air flow rate through the system. The analysis is sometimes made more complicated than it need be by the absence of appropriate data from manufacturers and the non-standard ways of expressing flow characteristics. The situation has been improved in recent years by the availability on the market of valves and cylinders to ISO standards.

The methods outlined here are offered as a practical way of circuit analysis and, as far as possible, are methods that are adopted by the majority of manufacturers.

Flow data for pneumatic valves

There may be a certain amount of confusion caused when reading manufacturers’ catalogues and trying to compare the data as presented.

In the past, the flow characteristics of pneumatic valves were determined by measuring the volume of water passing through them under pressure. This method produces a parameter known as the flow coefficient, K•. The definition of K. for a valve or other component is the flow in litres of water which passes through it with a pressure drop of 1 bar.

The corresponding value in American units is the flow in gallons per minute with a pressure drop of 1 lbf/in2 ; it is usually given the symbol C•. K. is related to C. by the relationship K.= 14.3C•. British data are sometimes quoted in terms oflmperial gallons, so it is important to check the basis of measurement, when a value for C. is quoted.

Under this system, the relationship between flow and pressure for pneumatic flow is given by:

The factor 0.47 has been introduced to allow for the change in density between water and air. q is the flow in litres and PI and P2 are the upstream and downstream pressures in bar.

Since this relationship has been developed for an incompressible fluid (water), it is only accurate for circumstances where the flow approximates to incompressible, ie where the density change through the valve is small, which implies a small pressure drop. For flow typical of a pneumatic valve supplying a cylinder, this is not usually the case, although it is applicable for valves on a main flow circuit, where a large pressure loss would be unacceptable. A valve feeding a cylinder will behave more often as an orifice, for which the orifice formulae will apply. Of course, for a small pressure drop, the orifice formula and the incompressible (square root) formula give the same result.

The basis of presenting valve flow data using the generalised form of the orifice formula has been discussed in the chapter on Pipe Flow Calculations, and manufacturers now usually adopt this method when giving flow data for valves. These data will have been determined experimentally in accordance with the method described in BS 5793, and so can be used with confidence.

Under this method, the equation for flow through a valve is given by the pair of

P1 and P2 are the upstream and downstream pressures respectively in bar (absolute) and q is the flow rate in litre/s. The value C is known as the conductance with units of litre/(s bar). b is the critical pressure ratio. Note that C is not the same as Cv.

In order to take account of the practical difference between a valve and a simple orifice, the values ofC and bare found experimentally and so, in general, they are different from the theoretical values that would be obtained from treating the valve as an orifice with an area equal to that of the minimum passage area through the valve. Failing any better information, the theoretical values for a sharp-edged orifice may be used. For air at l5°C they are:

It should be emphasised that the conversions for Care semi-empirical and should only be used when the correct values are not otherwise available. The value of C, however obtained, can only be used in the above equations to determine q and only if the correct units are used.

It is possible, knowing the value of C and b, to calculate the flow for any values of upstream and downstream pressure. For some purposes, eg when incorporated in a computer program, this may be the preferred option. In their catalogues, manufacturers often include sets of curves which can be used directly to find the flow rate. A sample of these curves is given in Figure 1.While the general shape is typical of all valves, the actual flow rates, even for the same nominal size, will vary from manufacturer to manufacturer. Valve characteristics in this form apply not only to selector valves but also to shut-off,

shuttle, check and restrictor valves. If used at a temperature significantly different from 20°C, a correction factor can be applied, although this is usually small.

Cylinder performance

The thrust available from an air cylinder is given by:

F is in newtons, Pis the gauge pressure in bar and A is the effective piston area in mm 2 •

f is the cylinder efficiency, taking into account seal friction.

A is the area of the piston when extending, or the area of the piston minus the area of the piston rod when contracting. f is usually taken as 0.75 (75% efficiency). One manufacturer quotes 0.8, except for cylinders larger in diameter than 100 mm, in which case, 0.65 is suggested.

The air consumption of a cylinder is:

q is in litre/s (free air), Pis the absolute pressure in bar, Lis the stroke in mm, A is the cross-section area in mm 2 and N is the frequency of operation in cycle/s. For single-acting cylinders (no return air), A is the piston area; for double-acting cylinders A is the sum of the piston area and the return area. This formula takes no account of the volume of air in the pipework or the clearance volume in the cylinder. It should be borne in mind that a cylinder frequently strokes through a shorter distance than the actual geometric stroke available. Ifthat is the case, then a wasted volume has to be filled both on the outward and inner strokes, and it should be taken into account in the calculation.

Manufacturers’ catalogues usually give tables of air consumption and thrust. These values are readily calculated and so are not reproduced here, but Figure 2 gives a ready method of determining the air consumed for a stroke of lO mm. Consumption for other strokes can be calculated by proportion.

Piston velocity

Calculation of piston velocity does present some problems, because it depends on an accurate estimate of the external loads on the piston. The following are the loads that might be present

• inertia loads caused by accelerating the mass attached to the piston,

• work load performed by the cylinder,

• friction,

• lifting or lowering a weight.

The sum of all these forces must be equated to the force across the piston.

Usually one of the design parameters is the cycle time, and this may mean the choice of a cylinder larger than that strictly necessary to apply the maximum load. The average force may not be the same as the maximum force. Once the pressure in the cylinder and the frequency of operation have been determined, the pressure drop across the valve can be found and a proper choice of valve made, using the valve data as explained above. It

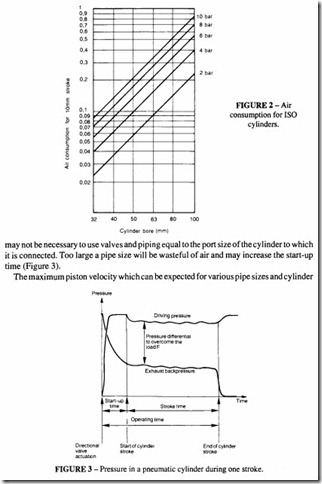
may not be necessary to use valves and piping equal to the port size of the cylinder to which it is connected. Too large a pipe size will be wasteful of air and may increase the start-up time (Figure 3).

The maximum piston velocity which can be expected for various pipe sizes and cylinder

Pressure

r-r–.. Driving pressure

Pressure differenttal to overcome the loadF

Exhaustbackpressuro

.

st; up 1 Time

Strokettme

Otrectional valve actuatton

1 Operating time

Start of cylinder

stroke

End of cylinder stroke

FIGURE 3- Pressure in a pneumatic cylinder during one stroke.

534 THE PNEUMATIC HANDBOOK

TABLE 1- Maxiumum piston velocity

These tables show the maximum piston velocity to be expected for various pipe sizes and cylinder bore sizes. The tables have been computed at 6 bar, and should be used as a general guide.

Actual velocities will depend on the length of pipe runs used, valves, fittings, etc.

bore sizes can be assessed from Table I. This is a guide only and should be used only in the absence of a full analysis. The table has been computed for a pressure of 6 bar.

Improving operational speed

If it should prove that the operating time of a cylinder is too long, there are various measures that should be considered to reduce it. If the pressure in the cylinder is close to the line pressure and the exhaust pressure is close to atmospheric, there is little one can do other than increase the supply pressure or change the cylinder diameter. Ifthe pressure on the power side of the cylinder is too low, consider:

• placing the main valve nearer to the cylinder port,

• introducing pilot operation if necessary,

• increase the size of the valve and pipework but no more than the port size of the cylinder.

Ifpressure on the exhaust side ofthe cylinder is too high, consider introducing a quick exhaust valve.

If the problem is too rapid an operating time, the preferred solution is the introduction of a restriction valve in the exhaust line.

Pressure limitations

The maximum safe working pressures for valves and cylinders are given by the manufac­ turers and should not be exceeded. The system opemting pressure is set at the compressor and air receiver by a pressure regulating valve and safety valve. As the air is compressible and is rarely stored at pressures much higher than I 0 bar, high peak pressures are seldom encountered as they are with hydraulic valves.

The development of higher working pressures requires an increasingly disproportion­ ate expenditure of power for compression, as well as increased component stresses and explosion hazard in the event off ailure. The difference between hydraulics and pneumat­ ics is due to the compressibility of the air.

For general applications, the only advantage offered by higher compression ratios is in storage systems, where air at high pressure can be stored in a smaller vessel and reduced to conventional delivery pressure when required.

For specialised applications such as rock drilling, air blasting and metal forming, higher pressures are called for.

The following pressure ranges can be distinguished:

• low pressure for conventional industrial pneumatics,

• moderate pressure (17 to 35 bar) derived from a compressor or reservoir charged from a compressor,

• high pressure derived from a charged air bottle,

• very high pressure derived from a high pressure receiver or intensifiers for small volume applications,

• ultra-high pressures supplied from multi-stage reciprocating compressors.

Incoming search terms:

• originj7x
• secondn54

Related posts: