ENERGY CONVERSION EFFICIENCIES
Efficiency is one of the most frequently used terms in thermodynamics, and it indicates how well an energy conversion or transfer process is accomplished. The thermal efficiency of a heat engine, for example, is the fraction of the thermal energy a heat engine converts to work. Efficiency is also one of the most frequently misused terms in thermodynamics and a source of misunderstandings. This is because efficiency is often used without being properly de- fined first. Next we will clarify this further, and define some efficiencies commonly used in practice.
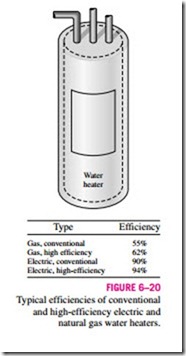
If you are shopping for a water heater, a knowledgeable salesperson will tell you that the efficiency of a conventional electric water heater is about 90 per- cent (Fig. 6–20). You may find this confusing, since the heating elements of electric water heaters are resistance heaters, and the efficiency of all resistance heaters is 100 percent as they convert all the electrical energy they consume into heat. A knowledgeable salesperson will clarify this by explaining that the heat losses from the hot-water tank to the surrounding air amount to 10 percent of the electrical energy consumed, and the efficiency of a water heater
is defined as the ratio of the energy delivered to the house by hot water to the energy supplied to the water heater. A clever salesperson may even talk you into buying a more expensive water heater with thicker insulation that has an efficiency of 94 percent. If you are a knowledgeable consumer and have access to natural gas, you will probably purchase a gas water heater whose efficiency is only 55 percent since a gas unit costs about the same as an electric unit to purchase and install, but the annual energy cost of a gas unit will be
less than half of that of an electric unit at national average electricity and gas prices.
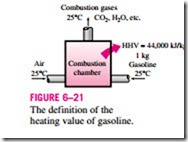
Perhaps you are wondering how the efficiency for a gas water heater is defined, and why it is much lower than the efficiency of an electric heater. As a general rule, the efficiency of equipment that involves the combustion of a fuel is based on the heating value of the fuel, which is the amount of heat released when a specified amount of fuel (usually a unit mass) at room temperature is completely burned and the combustion products are cooled to the room temperature (Fig. 6–21). Then the performance of combustion equipment can be characterized by combustion efficiency, defined as
A combustion efficiency of 100 percent indicates that the fuel is burned completely and the stack gases leave the combustion chamber at room temperature, and thus the amount of heat released during a combustion process is equal to the heating value of the fuel.
Most fuels contain hydrogen, which forms water when burned, and the heating value of a fuel will be different, depending on whether the water in combustion products is in the liquid or vapor form. The heating value is called the lower heating value, or LHV, when the water leaves as a vapor, and the higher heating value, or HHV, when the water in the combustion gases is completely condensed and thus the heat of vaporization is also recovered. The difference between these two heating values is equal to the product of the amount of water and the enthalpy of vaporization of water at room temperature. For ex- ample, the lower and higher heating values of gasoline are 44,000 kJ/kg and 47,300 kJ/kg, respectively. An efficiency definition should make it clear whether it is based on the higher or lower heating value of the fuel. Efficiencies of cars and jet engines are normally based on lower heating values since water normally leaves as a vapor in the exhaust gases, and it is not practical to try to recuperate the heat of vaporization. Efficiencies of furnaces, on the other hand, are based on higher heating values.
The efficiency of space heating systems of residential and commercial buildings is usually expressed in terms of the annual fuel utilization efficiency, or AFUE, which accounts for the combustion efficiency as well as other losses such as heat losses to unheated areas and start-up and cool-down losses. The AFUE of most new heating systems is close to 85 percent, al- though the AFUE of some old heating systems is under 60 percent. The AFUE of some new high-efficiency furnaces exceeds 96 percent, but the high cost of such furnaces cannot be justified for locations with mild to moderate winters. Such high efficiencies are achieved by reclaiming most of the heat in the flue gases, condensing the water vapor, and discharging the flue gases at temperatures as low as 38°C (or 100°F) instead of about 200°C (or 400°F) for the conventional models.
For car engines, the work output is understood to be the power delivered by the crankshaft. But for power plants, the work output can be the mechanical power at the turbine exit, or the electrical power output of the generator.
A generator is a device that converts mechanical energy to electrical energy, and the effectiveness of a generator is characterized by the generator efficiency, which is the ratio of the electrical power output to the mechanical
power input. The thermal efficiency of a power plant, which is of primary interest in thermodynamics, is usually defined as the ratio of the shaft work out- put of the turbine to the heat input to the working fluid. The effects of other factors are incorporated by defining an overall efficiency for the power plant as the ratio of the net electrical power output to the rate of fuel energy input. That is,
The overall efficiencies are about 26–30 percent for gasoline automotive engines, 34–40 percent for diesel engines, and 40–60 percent for large power plants.
Electrical energy is commonly converted to rotating mechanical energy by electric motors to drive fans, compressors, robot arms, car starters, and so forth. The effectiveness of this conversion process is characterized by the motor efficiency hmotor, which is the ratio of the mechanical energy output of the motor to the electrical energy input. The full-load motor efficiencies range from about 35 percent for small motors to over 96 percent for large high- efficiency motors. The difference between the electrical energy consumed and the mechanical energy delivered is dissipated as waste heat.
We are all familiar with the conversion of electrical energy to light by in- candescent lightbulbs, fluorescent tubes, and high-intensity discharge lamps. The efficiency for the conversion of electricity to light can be defined as the ratio of the energy converted to light to the electrical energy consumed. For example, common incandescent lightbulbs convert about 10 percent of the electrical energy they consume to light; the rest of the energy consumed is dissipated as heat, which adds to the cooling load of the air conditioner in summer. However, it is more common to express the effectiveness of this con- version process by lighting efficacy, which is defined as the amount of light output in lumens per W of electricity consumed.
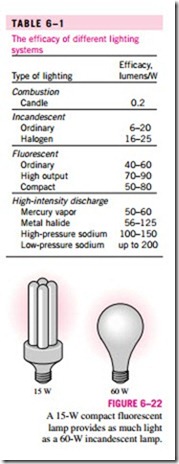
The efficacy of different lighting systems is given in Table 6–1. Note that a compact fluorescent lightbulb produces about four times as much light as an incandescent lightbulb per W, and thus a 15-W fluorescent bulb can replace a 60-W incandescent lightbulb (Fig. 6–22). Also, a compact fluorescent bulb lasts about 10,000 h, which is 10 times as long as an incandescent bulb, and it
plugs directly into the socket of an incandescent lamp. Therefore, despite their higher initial cost, compact fluorescents reduce the lighting costs considerably through reduced electricity consumption. Sodium-filled high-intensity dis- charge lamps provide the most efficient lighting, but their use is limited to out- door use because of their yellowish light.
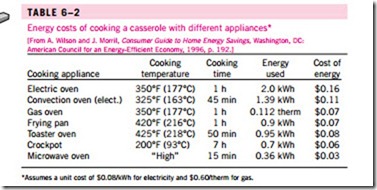
We can also define efficiency for cooking appliances since they convert electrical or chemical energy to heat for cooking. The efficiency of a cooking appliance can be defined as the ratio of the useful energy transferred to the food to the energy consumed by the appliance (Fig. 6–23). Electric ranges are more efficient than gas ranges, but it is much cheaper to cook with natural gas than with electricity because of the lower unit cost of natural gas (Table 6–2). The cooking efficiency depends on user habits as well as the individual appliances. Convection and microwave ovens are inherently more efficient than conventional ovens. On average, convection ovens save about one-third and microwave ovens save about two-thirds of the energy used by conventional
ovens. The cooking efficiency can be increased by using the smallest oven for baking, using a pressure cooker, using a crockpot for stews and soups, using the smallest pan that will do the job, using the smaller heating element for small pans on electric ranges, using flat-bottomed pans on electric burners to assure good contact, keeping burner drip pans clean and shiny, defrosting frozen foods in the refrigerator before cooking, avoiding preheating unless it is necessary, keeping the pans covered during cooking, using timers and thermometers to avoid overcooking, using the self-cleaning feature of ovens right after cooking, and keeping inside surfaces of microwave ovens clean.
Using energy-efficient appliances and practicing energy conservation mea- sures help our pocketbooks by reducing our utility bills. It will also help the environment by reducing the amount of pollutants emitted to the atmosphere during the combustion of fuel at home or at the power plants where electricity is generated. The combustion of each therm of natural gas produces 6.4 kg of carbon dioxide, which causes global climate change; 4.7 g of nitrogen oxides and 0.54 g of hydrocarbons, which cause smog; 2.0 g of carbon monoxide, which is toxic; and 0.030 g of sulfur dioxide, which causes acid rain. Each therm of natural gas saved eliminates the emission of these pollutants while saving $0.60 for the average consumer in the United States. Each kWh of electricity saved will save 0.4 kg of coal and 1.0 kg of CO2 and 15 g of SO2 from a coal power plant.