Thermodynamic cycles can be divided into two general categories: power cycles and refrigeration cycles.
The devices or systems used to produce a net power output are often called engines, and the thermodynamic cycles they operate on are called power cycles. The devices or systems used to produce refrigeration are called refrigerators, air conditioners, or heat pumps, and the cycles they operate on are called refrigeration cycles.
Thermodynamic cycles can also be categorized as gas cycles or vapor cycles, depending on the phase of the working fluid—the substance that circulates through the cyclic device. In gas cycles, the working fluid remains in the gaseous phase throughout the entire cycle, whereas in vapor cycles the working fluid exists in the vapor phase during one part of the cycle and in the liquid phase during another part.
Thermodynamic cycles can be categorized yet another way: closed and open cycles. In closed cycles, the working fluid is returned to the initial state at the end of the cycle and is recirculated. In open cycles, the working fluid is renewed at the end of each cycle instead of being recirculated. In automobile engines, for example, the combustion gases are exhausted and replaced by fresh air–fuel mixture at the end of each cycle. The engine operates on a me- chanical cycle, but the working fluid in this type of device does not go through a complete thermodynamic cycle.
Heat engines are categorized as internal combustion or external combustion engines, depending on how the heat is supplied to the working fluid. In external combustion engines (such as steam power plants), energy is supplied to the working fluid from an external source such as a furnace, a geothermal well, a nuclear reactor, or even the sun. In internal combustion engines (such as automobile engines), this is done by burning the fuel within the system boundary. In this chapter, various gas power cycles are analyzed under some simplifying assumptions.
Steam is the most common working fluid used in vapor power cycles because of its many desirable characteristics, such as low cost, availability, and high enthalpy of vaporization. Other working fluids used include sodium, potassium, and mercury for high-temperature applications and some organic fluids such as benzene and the freons for low-temperature applications.
Steam power plants are commonly referred to as coal plants, nuclear plants, or natural gas plants, depending on the type of fuel used to supply heat to the steam. But the steam goes through the same basic cycle in all of them. There- fore, all can be analyzed in the same manner.
The most frequently used refrigeration cycle is the vapor-compression refrigeration cycle in which the refrigerant is vaporized and condensed alternately and is compressed in the vapor phase.
■ BASIC CONSIDERATIONS IN THE ANALYSIS OF POWER CYCLES
Most power-producing devices operate on cycles, and the study of power cycles is an exciting and important part of thermodynamics. The cycles encountered in actual devices are difficult to analyze because of the presence of complicating effects, such as friction, and the absence of sufficient time for establishment of the equilibrium conditions during the cycle. To make an analytical study of a cycle feasible, we have to keep the complexities at a manageable level and utilize some idealizations (Fig. 8–1). When the actual cycle is stripped off all the internal irreversibilities and complexities, we end up with a cycle that resembles the actual cycle closely but is made up totally of internally reversible processes. Such a cycle is called an ideal cycle (Fig. 8–2).
A simple idealized model enables engineers to study the effects of the major parameters that dominate the cycle without getting bogged down in the details. The cycles discussed in this chapter are somewhat idealized, but they still retain the general characteristics of the actual cycles they represent. The conclusions reached from the analysis of ideal cycles are also applicable to actual cycles. The thermal efficiency of the Otto cycle, the ideal cycle for spark- ignition automobile engines, for example, increases with the compression ratio. This is also the case for actual automobile engines. The numerical values obtained from the analysis of an ideal cycle, however, are not necessarily representative of the actual cycles, and care should be exercised in their interpretation (Fig. 8–3). The simplified analysis presented in this chapter for various power cycles of practical interest may also serve as the starting point for a more in-depth study.
Heat engines are designed for the purpose of converting other forms of energy (usually in the form of heat) to work, and their performance is expressed in terms of the thermal efficiency hth, which is the ratio of the net work produced by the engine to the total heat input:
Recall that heat engines that operate on a totally reversible cycle, such as the Carnot cycle, have the highest thermal efficiency of all heat engines operating
between the same temperature levels. That is, nobody can develop a cycle more efficient than the Carnot cycle. Then this question arises naturally: If the Carnot cycle is the best possible cycle, why do we not use it as the model cycle for all the heat engines instead of bothering with several so-called ideal cycles? The answer to this question is hardware-related. Most cycles encountered in practice differ significantly from the Carnot cycle, which makes it un- suitable as a realistic model. Each ideal cycle discussed in this chapter is related to a specific work-producing device and is an idealized version of the actual cycle.
The ideal cycles are internally reversible, but, unlike the Carnot cycle, they are not necessarily externally reversible. That is, they may involve irreversibilities external to the system such as heat transfer through a finite temperature difference. Therefore, the thermal efficiency of an ideal cycle, in general, is less than that of a totally reversible cycle operating between the same temperature limits. However, it is still considerably higher than the thermal efficiency of an actual cycle because of the idealizations utilized (Fig. 8–4).
The idealizations and simplifications commonly employed in the analysis of power cycles can be summarized as follows:
1. The cycle does not involve any friction. Therefore, the working fluid does not experience any pressure drop as it flows in pipes or devices such as heat exchangers.
2. All expansion and compression processes take place in a quasi- equilibrium manner.
3. The pipes connecting the various components of a system are well insulated, and heat transfer through them is negligible.
Neglecting the changes in kinetic and potential energies of the working fluid is another commonly utilized simplification in the analysis of power
cycles. This is a reasonable assumption since in devices that involve shaft work, such as turbines, compressors, and pumps, the kinetic and potential energy terms are usually very small relative to the other terms in the energy equation. Fluid velocities encountered in devices such as condensers, boilers, and mixing chambers are typically low, and the fluid streams experience little change in their velocities, again making kinetic energy changes negligible. The only devices where the changes in kinetic energy are significant are the nozzles and diffusers, which are specifically designed to create large changes in velocity.
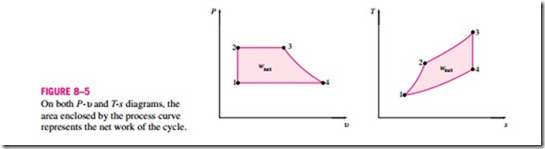
In the preceding chapters, property diagrams such as the P-υ and T–s dia- grams have served as valuable aids in the analysis of thermodynamic processes. On both the P-υ and T–s diagrams, the area enclosed by the process curves of a cycle represents the net work produced during the cycle (Fig. 8–5), which is also equivalent to the net heat transfer for that cycle. The T–s diagram is particularly useful as a visual aid in the analysis of ideal power cycles. An ideal power cycle does not involve any internal irreversibilities, and so the only effect that can change the entropy of the working fluid during a process is heat transfer.
On a T–s diagram, a heat-addition process proceeds in the direction of in- creasing entropy, a heat-rejection process proceeds in the direction of de- creasing entropy, and an isentropic (internally reversible, adiabatic) process proceeds at constant entropy. The area under the process curve on a T–s diagram represents the heat transfer for that process. The area under the heat addition process on a T–s diagram is a geometric measure of the total heat supplied during the cycle qin, and the area under the heat rejection process is a measure of the total heat rejected qout. The difference between these two (the area enclosed by the cyclic curve) is the net heat transfer, which is also the net work produced during the cycle. Therefore, on a T–s diagram, the ratio of the area enclosed by the cyclic curve to the area under the heat-addition process curve represents the thermal efficiency of the cycle. Any modification that will increase the ratio of these two areas will also improve the thermal efficiency of the cycle.
Although the working fluid in an ideal power cycle operates on a closed loop, the type of individual processes that comprises the cycle depends on the individual devices used to execute the cycle. In the Rankine cycle, which is the ideal cycle for steam power plants, the working fluid flows through a series of steady-flow devices such as the turbine and condenser, whereas in the Otto cycle, which is the ideal cycle for the spark-ignition automobile engine, the working fluid is alternately expanded and compressed in a piston-cylinder device. Therefore, equations pertaining to steady-flow systems should be used in the analysis of the Rankine cycle, and equations pertaining to closed systems should be used in the analysis of the Otto cycle.