Ampacity
A cable’s ampacity is the maximum continuous current rating of the cable. We should realize that while we may derive one number, say 480 A, for ampacity during normal operations for a given conductor, there is nothing magic about 480 A. The cable will not burst into flames at 481 A; the 480 A is simply a design number. We don’t want to exceed that current during normal operations.
The insulation temperature is normally the limiting factor. By operating below the ampacity of a given cable, we keep the cable insulation below its
recommended maximum temperature. Cross-linked polyethylene cables are rated for a maximum operating temperature of 90°C during normal opera- tions. Operating cables above their ampacity increases the likelihood of premature failures: water trees may grow faster, thermal runaway-failures are more likely, and insulation strength may decrease. In addition to absolute temperature, thermal cycling also ages cable more quickly.
Ampacity most often limits the loading on a cable; rarely, voltage drop or flicker limits loadings. Relative to overhead lines, cables of a given size have lower impedance and lower ampacities. So cable circuits are much less likely than overhead circuits to be voltage-drop limited. Only very long cable runs on circuits with low primary voltages are voltage-drop limited. Ampacity is not the only consideration for cable selection; losses and stocking consider- ations should also factor into cable selection. Choosing the smallest cable that meets ampacity requirements has the lowest initial cost, but since the cable is running hotter, the cost over its life may not be optimal because of the losses. Also allow for load growth when selecting cables.
Ampacity calculations follow simple principles: the temperature at the conductor is a function of the heat generated in a cable (I2R) and the amount of heat conducted away from the cable. We can model the thermal perfor- mance with a thermal circuit analogous to an electric circuit: heat is analo- gous to current; temperature to voltage; and thermal resistance to electrical resistance. Heat flow through a thermal resistance raises the temperature between the two sides of the thermal material. Higher resistance soils or insulations trap the heat and cause higher temperatures. Using the thermal equivalent of Ohm’s law, the temperature difference is:
Most ampacity tables and computer calculation routines are based on the classic paper by Neher and McGrath (1957). The original paper is an excellent reference. Ander’s book (1998) provides a detailed discussion of cable ampacity calculations, including the Neher–McGrath method along with IEC’s method that is very similar (IEC 287, 1982). Hand calculations or spreadsheet calculations of the Neher–McGrath equations are possible, but tiresome; while straightforward in principle, the calculations are very detailed. A review of the Neher–McGrath procedure — the inputs, the tech-
niques, the assumptions — provides a better understanding of ampacity calculations to better use computer ampacity calculations.
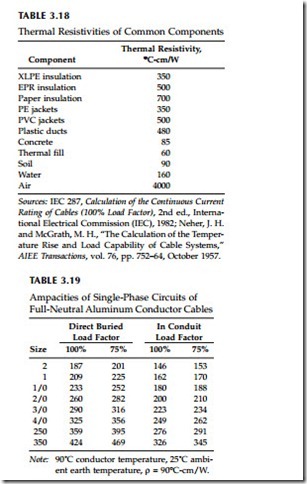
The Neher–McGrath procedure solves for the current in the equation above. Figure 3.9 shows a simplified model of the thermal circuit. The two main sources of heat within the cable are the I2R losses in the phase conductor and the I2R losses in the neutral or shield. The cable also has dielectric losses, but for distribution-class voltages, these are small enough that we can neglect them. The major thermal resistances are the insulation, the jacket, and the earth. If the cable system is in a duct, the air space within the duct and the duct walls adds thermal resistance. These thermal resistances are calculated from the thermal resistivities of the materials involved. For example, the thermal resistance of the insulation, jacket, and duct wall are all calculated with an equation of the following form:
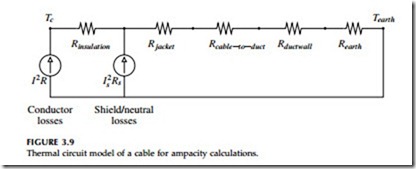
Thermal resistivity quantifies the insulating characteristics of a material. A material with r = 1°C-cm/W has a temperature rise of 1˚C across two sides of a 1-cm3 cube for a flow of one watt of heat through the cube. As with electrical resistivity, the inverse of thermal resistivity is thermal conductivity. Table 3.18 shows resistivities commonly used for cable system components. The thermal resistance of a material quantifies the radial tem- perature rise from the center outward. One thermal W-ft has a radial tem- perature rise of 1˚C for a heat flow of 1 W per ft of length (length along the conductor). Mixing of metric (SI) units with English units comes about for historical reasons.
The Neher–McGrath calculations also account for multiple cables, cables with cyclic daily load cycles, external heat sources, duct arrangements, and shield resistance and grounding variations.
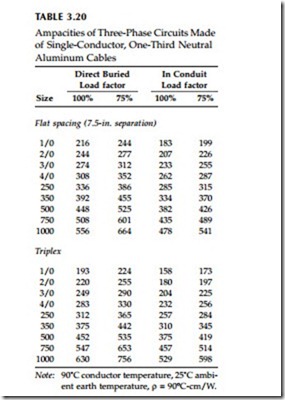
Often, the easiest way to find ampacities for a given application is with ampacity tables. Table 3.19 and Table 3.20 show ampacities for common distribution configurations. Of the many sources of ampacity tables, the IEEE publishes the most exhaustive set of tables (IEEE Std. 835-1994). The National Electrical Code (NFPA 70, 1999) and manufacturer’s publications (Okonite, 1990; Southwire Company, 1997) are also useful. Ampacity tables provide a
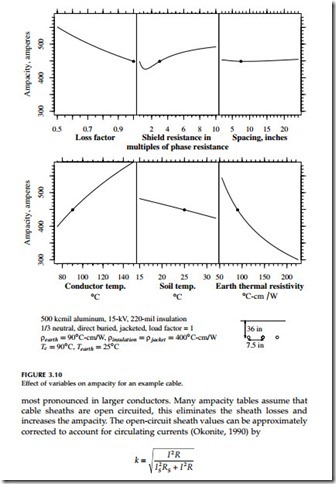
good starting point for determining the ampacity of a specific cable appli- cation. When using tables, be careful that the assumptions match your par- ticular situation; if not, ampacity results can be much different than expected. Conductor temperature limits, sheath resistance, thermal resistivity of the soil — these are some of the variables that most impact ampacity (see Figure 3.10). These and other effects are discussed in the next few paragraphs [see
also (CEA, 1982; NRECA RER Project 90-8, 1993) for more discussions].
Sheath resistance — On a three-phase circuit, the resistance of the sheath (or shield or neutral) plays an important role in ampacity calculations.
Because a cable’s phase conductor and sheath couple so tightly, current through the phase induces a large voltage along the sheath. With the cable sheath grounded periodically, circulating current flows to counter the induced voltage. The circulating current is a function of the resistance of the sheath. This circulating current leads to something counterintuitive: sheaths with higher resistance have more ampacity. Higher resistance sheaths reduce the circulating current and reduce the I2R losses in the sheath. This effect is
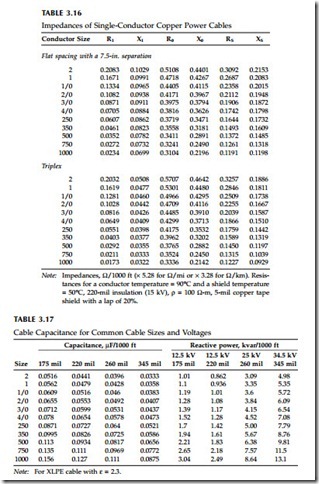
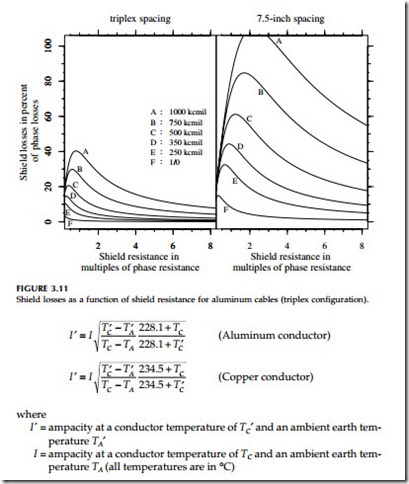
For configurations other than triplex, see Southwire Company (1997) or Okonite (1990). Figure 3.11 shows how sheath losses vary with conductor size and with spacing. Spacing has a pronounced effect. Steel ducts can significantly increase heating from circulating currents. In fact, even nearby steel pipes can significantly reduce ampacity.
Spacings — Separating cables separates the heat sources. But at larger spacings, circulating currents are higher. Optimal spacings involve balancing these effects. For smaller cables, separating cables provides the best ampacity. For larger cables (with larger circulating currents), triplex or other tight spacing improves ampacity. For one-third neutral, aluminum cables, NRECA (1993) shows that a flat spacing with 7.5 in. between cables has better ampac- ity than triplex for conductors 500 kcmil and smaller. For copper cables, the threshold is lower: conductors larger than 4/0 have better ampacity with a triplex configuration.
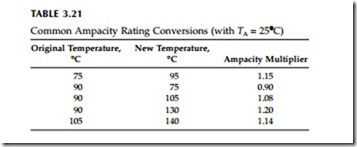
Conductor temperature — If we allow a higher conductor temperature, we can operate a cable at higher current. If we know the ampacity for a given conductor temperature, at a different conductor temperature we can find the ampacity with the following approximation:
We can use these equations to find emergency ampacity ratings of cables. In an emergency, XLPE can be operated to 130°C. Some EPR cables can be operated to 140°C (MV-105 cables). ICEA standards allow emergency over- load for 100 hours per year with five such periods over the life of the cable. Polyethylene cables, including HMWPE, have little overload capability. Their maximum recommended emergency temperature is 95°C. Table 3.21 shows common ampacity multipliers; these are valid for both copper and aluminum conductors within the accuracy shown. We can also use the
appropriate temperature-adjustment equation to adjust for different ambient earth temperatures.
Loss factor — The earth has a high thermal storage capability; it takes considerable time to heat (or cool) the soil surrounding the cable. Close to the cable, the peak heat generated in the cable determines the temperature drop; farther out, the average heat generated in the cable determines the temperature drop. As discussed in Chapter 5, we normally account for losses using the loss factor, which is the average losses divided by the peak losses. Since this number is not normally available, we find the loss factor from the load factor (the load factor is the average load divided by the peak load). Assuming a 100% load factor (continuous current) is most conserva- tive but can lead to a cable that is larger than necessary. We should try to err on the high side when estimating the load factor. A 75% load factor is commonly used.
Conduits — The air space in conduits or ducts significantly reduces ampac- ity. The air insulation barrier traps more heat in the cable. Direct-buried cables may have 10 to 25% higher ampacities. Although the less air the better, there is little practical difference in the thermal performance between the sizes of ducts commonly used. Concrete duct banks have roughly the same thermal performance as direct-buried conduits (concrete is more consistent and less prone to moisture fluctuations).
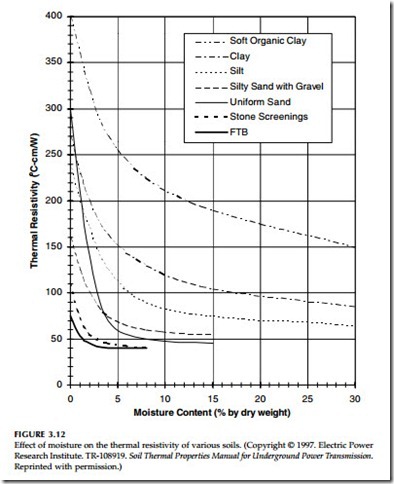
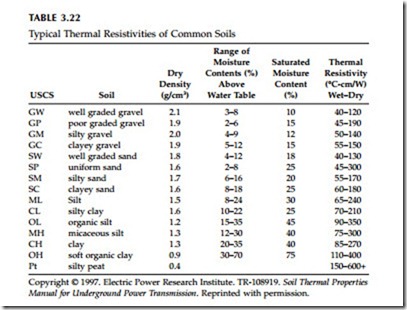
Soil thermal resistivity and temperature — Soils with lower thermal resistivity more readily conduct heat away from cables. Moisture is an important component, moist soil has lower thermal resistivity (see Figure 3.12). Dense soil normally has better conductivity. More so than any other single factor, soil resistivity impacts the conductor’s temperature and the cable’s ampac- ity. A resistivity of 90°C-cm/W is often assumed for ampacity calculations. This number is conservative enough for many areas, but if soil resistivities are higher, cable temperatures can be much higher than expected. For com- mon soils, Table 3.22 shows typical ranges of thermal resistivities. At typical installation depths, resistivity varies significantly with season as moisture content changes. Unfortunately in many locations, just when we need ampacity the most — during peak load in the summer — the soil is close to its hottest and driest. Seasonal changes can be significant, but daily
changes are not; soil temperature changes lag air temperature changes by 2 to 4 weeks.
The depth of burial can affect ampacity. With a constant resistivity and soil temperature, deeper burial decreases ampacity. But deeper, the soil tends to have lower temperature, more moisture, and soil is more stable seasonally. To go deep enough to take advantage of this is not cost effective though.
For areas with poor soil (high clay content in a dry area, for example), one of several thermal backfills can give good performance, with stable
resistivities below 60°C-cm/W even when moisture content drops below one percent.
Earth interface temperature — Because soil conductivity depends on mois- ture, the temperature at the interface between the cable or duct and the soil is important. Unfortunately, heat tends to push moisture away. High inter- face temperatures can dry out the surrounding soil, which further increases the soil’s thermal resistivity. Soil drying can lead to a runaway situation; hotter cable temperatures dry the soil more, raising the cable temperature more and so on. Some soils, especially clay, shrink significantly as it dries; the soil can pull away from the cable, leaving an insulating air layer. Thermal runaway can lead to immediate failure. Direct-buried cables are the most susceptible; ducts provide enough of a barrier that temperature is reduced by the time it reaches the soil.
Depending on the soil drying characteristics in an area, we may decide to limit earth interface temperatures. Limiting earth interface temperatures to 50 to 60°C reduces the risk of thermal runaway. But doing this also signifi- cantly decreases the ampacity of direct-buried cable to about that of cables in conduit. In fact, using the conduit ampacity values is a good approximation for the limits needed to keep interface temperatures in the 50 to 60°C range. Current unbalance — Almost every ampacity table (including those in this section) assumes balanced, three-phase currents. On multigrounded distri- bution systems, this assumption is rarely true. An ampacity of 100 A means a limit of 100 A on each conductor. Unbalance restricts the power a three-
phase cable circuit can carry (IA = IB = IC = 100 A carries more power than IA = 100 A, IB = IC = 70 A). In addition, the unbalanced return current may increase the heating in the cable carrying the highest current. It may or it may not; it depends on phase relationships and the phase angle of the unbalanced current. If the unbalances are just right, the unbalanced return current can significantly increase the neutral current on the most heavily loaded phases. Unbalance also depends on the placement of the cables. In a flat configuration, the middle cable is the most limiting because the outer two cables heat the middle cable.
Just as higher sheath resistances reduce circulating currents, higher sheath resistances reduce unbalance currents in the sheath. Higher sheath resis- tances force more of the unbalanced current to return in the earth. The heat generated in the sheath from unbalance current also decreases with increas- ing sheath resistance (except for very low sheath resistances, where the sheath has less resistance than the phase conductor).
System voltage and insulation thickness — Neither significantly impacts the ampacity of distribution cables. Ampacity stays constant with voltage; 5-kV cables have roughly the same ampacity as 35-kV cables. At higher voltages, insulation is thicker, but this rise in the thermal resistance of the insulation reduces the ampacity just slightly. Higher operating voltages also cause higher dielectric losses, but again, the effect is small (it is more noticeable with EPR cable).
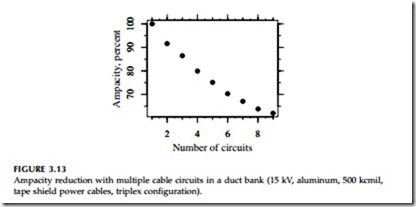
Number of cables — Cables in parallel heat each other, which restricts ampac- ity. Figure 3.13 shows an example for triplex power cables in duct banks.
Cable crossings and other hotspots — Tests have found that cable crossings can produce significant hotspots (Koch, 2001). Other hotspots can occur in locations where cables are paralleled for a short distance like taps to pad- mounted transformers or other gear. Differences in surface covering (such as asphalt roads) can also produce hot spots. Anders and Brakelmann (1999a, 1999b) provide an extension to the Neher–McGrath model that includes the effects of cable crossings at different angles. They conclude: “the derating of 3 to 5% used by some utilities may be insufficient, especially for cables with smaller conductors.”
Riser poles — Cables on a riser pole require special attention. The protective vertical conduit traps air, and the sun adds external heating. Hartlein and Black (1983) tested a specific riser configuration and developed an analytical model. They concluded that the size of the riser and the amount of venting were important. Large diameter risers vented at both ends are the best. With three cables in one riser, they found that the riser portion of the circuit limits the ampacity. This is especially important in substation exit cables and their riser poles. In a riser pole application, ampacity does not increase for lower load factors; a cable heats up much faster in the air than when buried in the ground (the air has little thermal storage). NRECA (1993) concluded that properly vented risers do not need to be derated, given that venting can increase ampacity between 10 and 25%. If risers are not vented, then the riser becomes the limiting factor. Additional work in this area has been done by Cress (1991) (tests and modeling for submarine cables in riser poles) and Anders (1996) (an updated analytical model).
Related posts:
Incoming search terms:
- distribution power cable ampacity ratings
- ampacity electrical distribution
- ug distribution ampacity rating
- triplex cable sheath circulating current
- thermal resistivity of soil table
- soil thermal resistivity table
- power distribution cable ampacities table
- power distribution cable ampacities
- ampacity underground cable cec 2015
- ampacity rating underground
- underground cable ampacities cec 2015