Statistical Characteristics of Aggregate Wind Power
It has only been within the last several years that aggregate wind power data sets have been made widely available to the research community. In this section we analyze several data sets with the goal of documenting and discussing statistical
characteristics of aggregate wind power, as well as seeking additional insight into geographic diversity.
Data Set Descriptions
Four data sets of aggregate wind power are considered: Bonneville Power Administration (BPA), Midwest ISO (MISO), PJM Interconnection (PJM), and 50 Hz [45–48]. BPA’s territory is located in the Pacific Northwest of the United States, primarily in Washington State and Oregon. MISO has territory in 12 states in the midwest of the United States and in the Canadian province of Manitoba. PJM’s territory covers all or parts of 13 states in the eastern portion of the U.S. 50 Hz’s territory is in the northern and eastern portion of Germany. Each system has a large amount of wind plant capacity.
The data correspond to hourly averages for the years 2008 and 2012. The data have been normalized to reported system-wide wind capacity. However, these reports are infrequently issued. To overcome this, linear interpolation between reporting dates was used. This inherently introduces some error in the analysis, and so the reported statistics must be interpreted with this in mind. The capacities at the start and end of 2008 and 2012 are provided in Table 1.
Statistical Analysis of Uncertainty
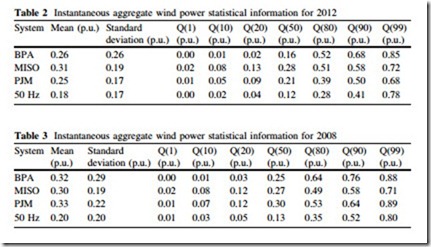
Several statistical quantities of instantaneous aggregate wind power for each system for 2012 and 2008 are provided in Tables 2 and 3, respectively. In addition to the mean and standard deviation, several quantiles were computed, where, for example, Q(50) refers to the median.
The mean values range between 0.18 and 0.33 p.u., and the standard deviation ranges from 0.17 to 0.29 p.u. These typical ranges of mean and standard deviation can be used to construct models of aggregate wind power, as discussed in Sect. 5.2. The Q(99) quantiles indicates the magnitude of rare wind power events. For example, for BPA in 2012, in 99 % of the hours the aggregate wind power was less than or equal to 85 % of the rated capacity. This means that 1 % of year— approximately 88 h—the power was greater than 0.85 p.u. For all systems, the values corresponding to the 99 % quantile ranged between 0.68 and 0.88 p.u. Extremely low values were common: the 10 % quantile is 0.08 p.u. or less in all cases. In other words, in each system the power output is less than 8 % of rated capacity for nearly 876 h each year. The relatively high frequency of low power output has system-wide generation capacity implications. In general, the systems have very different levels of uncertainty that must be managed by their operators. By several measures, MISO, PJM, and 50 Hz have less uncertainty than BPA.
Statistical Analysis of Variability
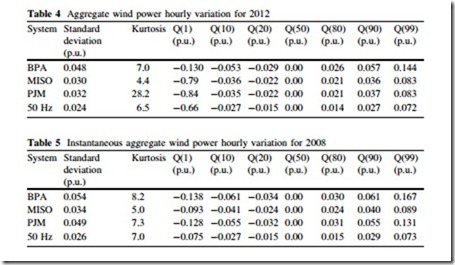
The statistics for hour-to-hour variation for each system in 2012 and 2008 are provided in Tables 4 and 5, respectively. The variations of aggregate wind power
in large systems tend to be symmetric, with near-zero mean and median. In most system, the variations are less than 0.06 p.u. in magnitude for over 80 % of the hours. Extreme outliers corresponding to changes of ± 0:08 to 0.17 p.u. do occur, but are rare. The standard deviations range from 0.024 to 0.054 p.u. In each system, the variations are leptokurtic, indicating a higher occurrence of ‘‘tail event’’ variations. In general, MISO, PJM, and 50 Hz have less variability than BPA.
Effect of Capacity on Uncertainty and Variability
The effect of capacity and capacity increases on aggregate wind power uncertainty and variability are often of interest as system operators anticipate and plan for increased amounts of wind plants in their system. The specifics of how the uncertainty and variability associated with aggregate wind power are related to capacity depend on the build-out of the wind plants in the system, and are difficult to analytically derive. However, based on the available data and past experience, there are several general observations that can be made:
1. Systems with larger installed capacities do not necessarily exhibit less uncertainty and variability in aggregate wind power than systems with smaller capacities.
2. Additions of wind plant capacity to a system tend reduce uncertainty and variability.
3. Within a given system, the benefits of geographic diversity can become saturated and insensitive to increases in capacity.
As an example of the first observation, we compare the statistics of instantaneous power in PJM and BPA. At the end of 2012, there was 4.7 GW of installed wind capacity in BPA. At the end of 2008 in PJM there was 1.3 GW of installed wind capacity. It would seem that BPA should have less uncertainty given its much higher installed capacity and therefore greater opportunity for geographic diversity. However, the standard deviation of PJM (0.22 p.u.) was less than that of BPA (26 p.u.). BPA also generally exhibited more occurrences of extremely low and high power production, as shown by the quantiles in Tables 2 and 3. A similar example for variability can be made by comparing 2008 MISO data with 2008 BPA data. These cases should not be misinterpreted as evidence that systems with higher capacities of wind plants have greater uncertainty and variability than those with lower capacities. Rather, they are simply examples that the contrary is not always the case. The important concept is that different systems experience different build- outs of wind plants—some lead to appreciable geographic diversity, others do not.
The second observation—that additions of wind plant capacity to a system tend reduce uncertainty and variability—is observed by comparing the statistics of each system in 2008–2012. In each system, the standard deviation of the instantaneous power and power variation decreased from 2008 to 2012. The exception is MISO, whose standard deviation of instantaneous power remained the same. Regardless, the data support the general notion that wind plant capacity additions decrease uncertainty and variability.
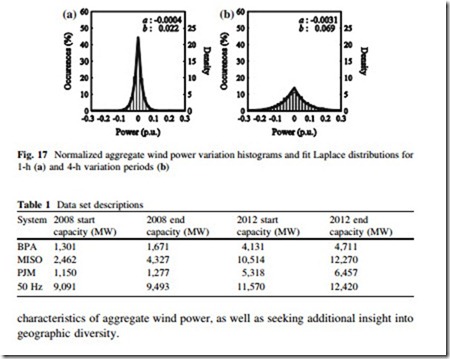
The final observation—that the benefits of uncertainty and variability reduction can become saturated—is supported by examining the sensitivity of uncertainty and variability to capacity addition. For BPA, PJM and 50 Hz, for every 1 GW of new wind plant installations, the standard deviation of instantaneous wind power decreased by just one percentage point, based upon year-end capacity values. For MISO, the standard deviation did not change, despite an increase in 8 GW of wind power. The quantiles in many systems also showed modest changes despite large capacity additions. The modest effects of capacity additions on uncertainty can be seen by inspecting Figs. 13 and 14. The histograms and approximated probability density functions of the system do not appear appreciably different in 2012 than they did in 2008, despite several thousand megawatts of wind plant installations in each system. The histograms and probability density functions of variations in Figs. 15 and 16, however, have more noticeable differences.
The sensitivity of variability to changes in capacity are mixed. The standard deviation of wind power variability in BPA and PJM decreased by approximately 0.25 % point for each 1 GW of new capacity. A change in percentage point of this magnitude is appreciable since the standard deviations of variation are all less than 6 %. However, both MISO and 50 Hz exhibited small changes to their standard deviation between 2008 and 2012.