Single-phase motors:Equivalent Circuit of a Single-phase Induction Motor–Without Core Loss and Equivalent Circuit–With Core Loss

Equivalent Circuit of a Single-phase Induction Motor–Without Core Loss

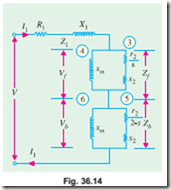
A single-phase motor may be looked upon as consisting of two motors, having a common stator winding, but with their respective rotors revolving in opposite directions. The equivalent circuit of such a motor based on double-field revolving theory is shown in Fig. 36.14. Here, the single- phase motor has been imagined to be made-up of (i) one stator winding and (ii) two imaginary rotors. The stator impedance is Z = R1 + j X1. The impedance of each rotor is (r2 + jx2) where r2 and x2 represent half the actual rotor values in stator terms (i.e. x2 stands for half the standstill reactance of the rotor, as referred to stator). Since iron loss has been neglected, the exciting branch is shown consisting of exciting reactance only. Each rotor has been assigned half the magnetising reactance* (i.e xm represents half the actual reactance). The

and it runs with a slip of s. The impedance of ‘backward’ running rotor is

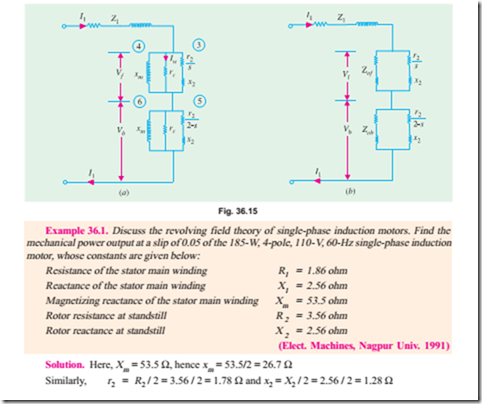
Equivalent Circuit–With Core Loss

The core loss can be represented by an equivalent resistance which may be connected either in parallel or in series with the magnetising reactance as shown in Fig. 36.15.

Since under running conditions V f is very high (and V b is correspondingly, low) most of the iron loss takes place in the ‘forward motor’ consisting of the common stator and forward-running rotor. Core-loss current Iw = core loss / V f. Hence, half value of core-loss equivalent resistance is rc = V f / Iw. As shown in Fig. 36.15 (a), rc has been connected in parallel with xm in each rotor.

Tutorial Problem No. 36.1.

1. A 1-f, induction motor has stator windings in space quadrature and is supplied with a single-phase voltage of 200 V at 50 Hz. The standstill impedance of the main winding is (5.2 + j 10.1) and of the auxiliary winding is (19.7 + j 14.2). Find the value of capitance to be inserted in the auxiliary winding for maximum starting torque.

 (Electrical Machines-III, Indore Univ. July, 1977)

2. A 230-V, 50-Hz, 6-pole, single-phase induction motor has the following constants.

r1 = 0.12 W, r2 = 0.14 W, x1 = x2 = 0.25 W, xm = 15 W.

If the core loss is 250 W and friction and windage losses are 500 W, determine the efficiency and torque at s = 0.05.

(Electrical Machines-IV, Bangalore Univ. Aug. 1978)

3. Explain how the pulsating mmf of a single-phase induction motor may be considered equivalent to two oppositely-rotating fields. Develop an expression for the torque of the motor.

A 125-W, 4-pole, 110-V, 50-Hz single-phase induction motor has the no-load rotational loss of 25 watts and total rotor copper loss at rated load of 25 watts at a slip of 0.06. The rotor I2R loss may be neglected.

At a slip s = 0.06, what is the power input to the machine ?

(Electrical Machines-III, Indore Univ. July 1977)

Incoming search terms:

• equivalent circuit of single phase induction motor
• equivalent circuit of single phase induction motor theory
• equivalent circuit of a single phase induction motor without core loss
• without core losses
• thoery of equiavalent ckt of 1phase induction motor
• theory of equivalent circuit of 1 phase induction motor
• losses in 1 phase inductio motor
• equivalent circuit of 1 phase induction motor
• equivalent circuit of 1 phase induction motor theory
• equivalent ckt 1 phase induction
• equivalent circuit of single phase induction motor with core loss and without coreloss
• single phase induction machine equivalent circuit
• equivalent circuit diagram of single phase induction motor
• single phase induction motor without core loss
• equivalent circuit of a single phase induction motor
• single phase induction motor equivalent circuit
• obtain equivalent circuit of single phase induction motor
• how to find xm in equivalent circuit diagram of induction motor
• how to find the value of xm in core loss
• how R1 find in equivalent circuit of single phase induction motor
• half value of core loss equivalent resistance of single phase induction motor
• explain equivalent circuit diagram of 1 phase induction motor at stand still and rotor running condition
• theory for equivalent circuit of 1-phase induction motor
• single phase induction motor equivalent circiut diagram
• partsl7z
• problems on equivalent circuit of single phase induction motor
• problems on single phase induction motor
• single phase induction motor tutorial
• single phase induction motor equivalent circuit question
• single phase capacitor motor equivalent
• explain about equivalent circuit diagram of one phase induction motor
• equvivalent circuit of single phase induction motor
• equivalent circuit of single phase induction motor calculations
• equivalent circuit of single phase induction motor calculation of values of r1 and r2
• equivalent circuit of single phase i m
• Equivalent circuit of a single phase i
• equivalent circuit for single phase induction motor
• draw circuit of single phase induction motor with and without core losses
• different of stator and rotor core loss in induction motor
• development of equivalent circuit of a single phase induction motor
• equivalent circuit of single phase induction motor with help of double field revolving theory
• equivalent circuit of single phase motor with core loss
• equvalent circuit of single phase induction
• equivent ckt of single phase induction motor with core loss
• equivalent ckt of single phase single winding with double revolving theory
• equivalent ckt of single phase induction motor
• equivalent ckt of 1ph
• equivalent ckt based on double revolving field theory
• equivalent ciruit of a single phase induction motor
• Equivalent circuit with core loss of an induction motor