Part 3: Communications
Let’s say I have a box containing all the knowledge in the world. How much would you pay me for it? Oh, one more thing. It’s a sealed box and nothing you can do will open it. Nothing, not now or ever. It has no hinges or even a lid. You can’t saw the top off or even bore a hole through one of the sides. It resists all acids, nuclear explosions, even Superman’s X-ray eyes. It is just an unopenable, sealed box that I absolutely guarantee you is filled with the answers to all your questions and all those of everyone else in the world. And it’s a nifty box, oak-oiled a nice, rich brown.
I’d guess you might offer a few dollars, whatever its decorative value. You might even eye it for seating if you didn’t have a chair (though I have to admit that the box is not all that big—and it sounds pretty empty at that). Basically, the value of all that knowledge is nothing if you can’t get at it and use it.
What would your computer be worth to you if you couldn’t get your answers out? If you couldn’t connect with the Internet? If you couldn’t plug in a CD writer or even a printer? I’d wager not much. It’s even an uncomfortable flop as a chair.
Fortunately, your computer is not resistant to a handsaw or electric drill. You can even open it up with a screwdriver. Better still, you can simply plug in a cable or two and connect up with another computer, a network, the Internet, or an Erector set. Your computer is a superlative communications machine. That’s what gives it its value—unless you really are using yours as a chair.
A computer communicates in many ways, both outside and inside its box. Moving information around electronically takes a lot of ingenuity and some pretty amazing technologies. Your system’s microprocessor must organize its thoughts, make them into messages that it can send out through its ports or down the wires that make up its expansion bus. It needs to know how to talk and, more importantly, how to listen. It needs to put the signals in a form that other computers and add-on devices (peripherals) can understand—a form that can travel a few inches across a circuit board, tens of thousands of miles through thin copper wires, or as blips of light in a fiber-optic cable. And it has to do all that without making a mistake.
The next seven chapters outline how your computer communicates. We’ll start out with the concepts that underlie all computer (and, for that matter, electronic) communications. From there, we’ll step into the real world and examine how your system talks to itself, sending messages inside its own case to other devices you might install there. We’ll look at the interfaces it uses to send messages—the computer’s equivalent of a telephone handset that it speaks and listens through. Then we’ll examine how it connects to external devices, all the accessories and peripherals you plug in. From there, we’ll examine the technologies that allow you to connect to the most important peripherals of all—other computers—both in your home or office on a network, and elsewhere in the world through the Internet.
There’s a lot to explore, so you might as well put your feet up. After all, a computer may not work well as a chair, but it can be a pretty good footstool.
Chapter 8. Channels and Coding
Communications is all about language and, unfortunately, understanding computer communications requires learning another language, one that explains the technology that allows us to send messages, music, and even pictures electronically.
We’re going to talk about channels, which are nothing more than the paths your electronic messages take. A communication channel is like a television channel. More than that, a television channel is a communication channel—a designated pathway for the television signal to get from the broadcasting station to your antenna and television set.
Different channels require technologies for moving information. Paper mail is a communication channel that requires you to use ink and paper (maybe a pencil in a pinch). Electronic communication requires that you translate your message into electronic form.
You cannot directly read an electronic message, no more than you could read it were it written in a secret code. In fact, when your message becomes electronic, it is written in a nonsecret code. Although human beings cannot read it, computers can, because some aspects of the signal correspond to the information in your message, exactly as code letters correspond to the text of a secret message.
As background for understanding how computer communications work, we’re first going to look at the characteristics and limitations of the channels that your computer might use. Then we’ll take a look at some of the ways that signals get coded so they can be passed through those channels—first as expansion buses inside your computer, then as serial and parallel communication channels between computers. Note that this coding of data is an important technology that has wide applications. It’s useful not only in communications but also data storage.
Signal Characteristics
Communications simply means getting information—be it your dulcet voice, a sheaf of your most intimate thoughts, or digital data—from one place to another. It could involve yelling into the wind, smoke signals, express riders on horseback, telegraph keys, laser beams, or whatever technology currently holds favor. Even before people learned to speak, they gestured and grunted to communicate with one another. Although today many people don’t do much more than that, we do have a modern array of technologies for moving our thoughts and feelings from one point to another to share with others or for posterity. Computers change neither the need for, nor purpose of, communications. Instead, they offer alternatives and challenges.
Thanks to computer technology, you can move not only your words but also images—both still and moving—at the speed of light. Anything that can be reduced to digital form moves along with computer signals. But the challenge is getting what you want to communicate into digital form, a challenge we won’t face until we delve into Part 5, “Human Interface.”
Even in digital form, communications can be a challenge.
Channels
If you were Emperor of the Universe, you could solve one of the biggest challenges in communications simply by forbidding anyone else to send messages. You would have every frequency in the airwaves and all the signal capacity of every wire and optic cable available to you. You wouldn’t have to worry about interference because should someone interfere with your communications, you could just play the Red Queen and shout “Off with their heads!” Alas, if your not Emperor of the Universe, someone may take a dim view of your hogging the airwaves and severing the heads of friends and family. Worse yet, you’re forced to do the most unnatural of acts—actually sharing your means of communication.
Our somewhat civilized societies have created a way to make sharing more orderly if not fair—dividing the space available for communications into channels. Each television and radio station, for example, gets a range of frequencies in which to locate its signals.
But a communications channel is something more general. It is any path through which you can send your signals. For example, when you make a telephone connection, you’ve established a channel.
Although there are regulatory systems to ensure that channels get fairly shared, all channels are not created equal. Some have room for more signals or more information than others. The channel used by a telephone allows only a small trickle of information to flow (which is why telephone calls sound so tinny). A fiber optic cable, on the other hand, has an immense space for information, so much that it is usually sliced into several hundred or thousand channels.
Bandwidth
The primary limit on any communications channel is its bandwidth, the chief constraint on the data rate through that channel. Bandwidth merely specifies a range of frequencies from the lowest to the highest that the channel can carry or present in the signal. It’s like your stereo system. Turn the bass (the low frequencies) and the treble (the high frequencies) all the way down, and you’ve limited the bandwidth to the middle frequencies. It doesn’t sound very good because you’re missing part of the signal—you’ve reduced its bandwidth.
Bandwidth is one way of describing the maximum amount of information that the channel can carry. Bandwidth is expressed differently for analog and digital circuits. In analog technology, the bandwidth of a circuit is the difference between the lowest and highest frequencies that can pass through the channel. Engineers measure analog bandwidth in kilohertz or megahertz. In a digital circuit, the bandwidth is the amount of information that can pass through the channel. Engineers measure digital bandwidth in bits, kilobits, or megabits per second. The kilohertz of an analog bandwidth and the kilobits per second of digital bandwidth for the same circuit are not necessarily the same and often differ greatly.
Nature conspires with the laws of physics to limit the bandwidth of most communications channels. Although an ideal wire should be able to carry any and every frequency, real wires cannot. Electrical signals are social busybodies of the physical world. They interact with themselves, other signals, and nearly everything else in the world—and all these interactions limit bandwidth. The longer the wire, the more chance there is for interaction, and the lower the bandwidth the wire allows. Certain physical characteristics of wires cause degradations in their high frequency transmission capabilities. The capacitance between conductors in a cable pair, for instance, increasingly degrades signals as their frequencies rise, finally reaching a point that a high frequency signal might not be able to traverse more than a few centimeters of wire. Amplifiers or repeaters, which boost signals so that they can travel longer distances, often cannot handle very low or very high frequencies, thus imposing more limits.
Even fiber optic cables, which have bandwidths dozens of times that of copper wires, also degrade signals with distance—pulses of light blur a bit as they travel through the fiber, until equipment can no longer pick digital bits from the blur.
Emissions Limitations
Even the wires inside computers have bandwidth limitations, although they are infrequently explicitly discussed as such. Every wire, even the copper traces on circuit boards (which act as wires), not only carries electricity but also acts as a miniature radio antenna. It’s unavoidable physics—moving electricity always creates a magnetic field that can radiate away as radio waves.
The closer the length of a wire matches the wavelength of an electrical signal, the better it acts as an antenna. Because radio waves are really long at low frequencies (at one megahertz, the wavelength is about 1000 feet long), radio emissions are not much of a problem at low frequencies. But today’s computers push frequencies into the gigahertz range, and their short wavelengths make ordinary wires and circuit traces into pretty good antennas. Engineers designing modern computers have to be radio engineers as well as electrical engineers.
Good designs cause fewer emissions. For example, engineers can arrange circuits so the signals they emit tend to cancel out. But the best way to minimize problems is to keep frequencies lower.
Lower frequencies, of course, limit bandwidth. But when you’re working inside a computer, there’s an easy way around that—increase the number of channels by using several in parallel. That expedient is the basis for the bus, a collection of several signals traveling in parallel, both electrically and physically. A computer expansion bus uses 8, 16, 32, or 64 separate signal pathways, thus lowering the operating frequency to a fraction of that required by putting all the data into a single, serial channel.
Standards-Based Limitations
The airwaves also have a wide bandwidth, and they are not bothered by radiation issues. After all, the signals in the airwaves are radiation. Nor are they bothered by signal degradation (except at certain frequencies where physical objects can block signals). But because radio signals tend to go everywhere, bandwidth through the airwaves is limited by the old bugaboo of sharing. To permit as many people to share the airwaves as possible, channels are assigned to arbitrarily defined frequency bands.
Sharing also applies to wire- and cable-based communications. Most telephone channels, for example, have an artificial bandwidth limitation imposed by the telephone company. To get the greatest financial potential from the capacity of their transmissions cables, microwave systems, and satellites, telephone carriers normally limit the bandwidth of telephone signals to a narrow slice of the full human voice range. That’s why phone calls have their unmistakable sound. By restricting the bandwidth of each call, the telephone company can stack many calls on top of one another using an electronic technique called multiplexing. This strategy allows a single pair of wires to carry hundreds of simultaneous conversations.
The real issue is not how signals get constrained by bandwidth, but rather the effect of bandwidth on the signal. Bandwidth constrains the ability of a channel to carry information. The narrower the bandwidth, the less information that gets through. It doesn’t matter whether the signal is analog or digital, your voice, a television picture, or computer data. The bandwidth of the channel will constrain the actual information of any signal passing through the channel.
Bandwidth limits appear wherever signals must go. Even the signals flowing from one part of a circuit to another inside a computer are constrained by bandwidth limits.
Modulation
Computers and the standard international communications systems grew up independently, each with its own technological basis. Computers began their commercial lives as digital devices because of the wonderful ability of digital signals to resist errors. Communications systems started on a foundation of analog technology. Their primary focus began as the transmission of the human voice, which was most easily communicated in analog form with the primitive technologies then available. Since the early days of computers and communications, the two technologies have become intimately intertwined: Computers have become communications engines, and most communications are now routed by computers. Despite this convergence, however, the two technologies remain stuck with their incompatible foundations—computers are digital and human communications are analog.
The technology that allows modems to send digital signals through the analog communications circuits is called modulation. The modulation process creates analog signals that contain all the digital information of the original digital computer code but which can be transmitted through the analog circuits, such as the voice-only channels of the telephone system.
Someday the incompatibility between the computer and communications worlds will end, perhaps sooner than you might think. In the year 2000, computer data overtook the human voice as the leading use of long-distance communications. Even before that, nearly all long distance voice circuits had been converted to use digital signals. But these changes haven’t eliminated the need for using modulation technology. Dial-up telephone lines remain the way most people connect their computers to the Internet, and local loops (the wires from the telephone company central office to your home) remain stubbornly analog. Moreover, many types of communications media (for example, radio waves) require modulation technology to carry digital (and even voice and music) signals.
The modulation process begins with a constant signal called the carrier, which carries or bears the load of the digital information. The digital data in some ways modifies the carrier, changing some aspect of it in such a way the change can be later detected in receiving equipment. The changes to the carrier—the information content of the signal—are the modulation, and the data is said to “modulate the carrier.”
Demodulation is the signal-recovery process, the opposite of modulation. During demodulation, the carrier is stripped away and the encoded information is returned to its original form. Although logically just the compliment of modulation, demodulation usually involves entirely different circuits and operating principles.
In most modulation systems, the carrier is a steady-state signal of constant amplitude (strength), frequency, and coherent phase—the electrical equivalent of a pure tone. Because it is unchanging, the carrier itself is devoid of content and information. It’s the equivalent of one, unchanging digital bit. The carrier is simply a package, like a milk carton for holding information. Although you need both the carrier and milk carton to move its contents from one place to another, the package doesn’t affect the contents and is essentially irrelevant to the product. You throw it away once you’ve got the product where you want it.
The most common piece of equipment you connect to your computer that uses modulation is the modem. In fact, the very name modem is derived from this term and the reciprocal circuit—the demodulator—that’s used in reception. Modem is a foreshortening of the words modulator and demodulator.
A modem modulates an analog signal that can travel through the telephone system with the digital direct current signals produced by your computer. The modem also demodulates incoming signals, stripping off the analog component and passing the digital information to your computer. The resulting modulated carrier wave remains an analog signal that, usually, whisks easily through the telephone system.
Radio systems also rely on modulation. They apply voice, video, or data information to a carrier wave. Radio works because engineers created receivers, which can tune to the frequency of the carrier and exclude other frequencies, so you can tune in to only the signal (and modulation) you want to receive. Note that most commonly, radio systems use analog signals to modulate their carriers. The modulation need not be digital.
The modulation process has two requirements. The first is the continued compatibility with the communications medium so that the signal is still useful. The second is the ability to separate the modulation from the carrier so that you can recover the original signal.
Just as AM and FM radio stations use different modulation methods to achieve the same end, designers of communications systems can select from several modulation technologies to encode digital data in a form compatible with analog transmission systems. The different forms of modulation are distinguished by the characteristics of the carrier wave that are changed in response to changes in data to encode information. The three primary characteristics of a carrier wave that designers might elect to vary for modulation are its amplitude, its frequency, and its phase. Pulse modulation is actually a digital signal that emulates an analog signal and can be handled by communications systems as it if it were one.
Carrier Wave Modulation
The easiest way to understand the technique of modulation is to look at its simplest form, carrier wave modulation, which is often abbreviated as CW, particularly by radio broadcasters.
As noted previously, a digital signal, when stripped to its essential quality, is nothing more than a series of bits of information that can be encoded in any of a variety of forms. We use zeros and ones to express digital values on paper. In digital circuits, the same bits take the form of the high and low direct current voltages, the same ones that are incompatible with the telephone system. However, we can just as easily convert digital bits into the presence or absence of a signal that can travel through the telephone system (or that can be broadcast as a radio wave). The compatible signal is, of course, the carrier wave. By switching the carrier wave off and on, we can encode digital zeroes and ones with it.
The resulting CW signal looks like interrupted bursts of round sine waves, as shown in Figure 8.1.
The figure shows the most straightforward way to visualize the conversion between digital and analog, assigning one full wave of the carrier to represent a digital one (1) and the absence of a wave to represent a zero (0). In most practical simple carrier waves systems, however, each bit occupies the space of several waves. The system codes the digital information not as pulses per se, but as time. A bit lasts a given period regardless of the number of cycles occurring within that period, making the frequency of the carrier wave irrelevant to the information content.
Although CW modulation has its shortcomings, particularly in wire-based communications, it retains a practical application in radio transmission. It is used in the simplest radio transmission methods, typically for sending messages in Morse code.
One of the biggest drawbacks of carrier wave modulation is ambiguity. Any interruption in the signal may be misinterpreted as a digital zero. In telephone systems, the problem is particularly pernicious. Equipment has no way of discerning whether a long gap between bursts of carrier wave is actually significant data or a break in or end of the message.
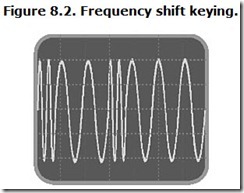
Frequency Shift Keying
A more reliable way of signaling digital information is to use separate and distinct frequencies for each digital state. For example, a digital 1 would cause the carrier wave to change to a higher frequency, much as it causes a higher voltage, and a digital 0 would shift the signal to a lower frequency. Two different frequencies and the shifts between them could then encode binary data for transmission across an analog system. This form of modulation is called frequency shift keying, or FSK, because information is encoded in (think of it being “keyed to”) the shifting of frequency.
The “keying” part of the name is actually left over from the days of the telegraph when this form of modulation was used for transmitting Morse code. The frequency shift came with the banging of the telegraph key.
In practical FSK systems, the two shifting frequencies are the modulation that is applied to a separate (and usually much higher) carrier wave. When no modulation is present, only the carrier wave at its fundamental frequency appears. With modulation, the overall signal jumps between two different frequencies. Figure 8.2 shows what an FSK modulation looks like electrically.
Frequency shift keying unambiguously distinguishes between proper code and a loss of signal. In FSK, a carrier remains present even when no code is being actively transmitted. FSK is thus more reliable than CW and more widely used in communications systems. The very earliest of computer modems (those following the Bell 103 standard) used ordinary FSK to put digital signals on analog telephone lines.
Amplitude Modulation
Carrier wave modulation is actually a special case of amplitude modulation. Amplitude is the strength of the signal or the loudness of a tone carried through a transmission medium, such as the telephone wire. Varying the strength of the carrier in response to modulation to transmit information is called amplitude modulation. Instead of simply being switched on and off, as with carrier wave modulation, in amplitude modulation the carrier tone gets louder or softer in response to the modulating signal. Figure 8.3 shows what an amplitude modulated signal looks like electrically.
Amplitude modulation is most commonly used by radio and television broadcasters to transmit analog signals because the carrier can be modulated in a continuous manner, matching the raw analog signal. Although amplitude modulation carries talk and music to your AM radio and the picture to your (nondigital) television set, engineers also exploit amplitude modulation for digital transmissions. They can, for example, assign one amplitude to indicate a logical 1 and another amplitude to indicate a logical 0.
Pure amplitude modulation has one big weakness. The loudness of a signal is the characteristic most likely to vary during transmission. Extraneous signals add to the carrier and mimic modulation. Noise in the communication channel line mimics amplitude modulation and might be confused with data.
Frequency Modulation
Just as amplitude modulation is a refinement of CW, frequency shift keying is a special case of the more general technology called frequency modulation. In the classic frequency modulation system used by FM radio, variations in the loudness of sound modulate a carrier wave by changing its frequency. When music on an FM station gets louder, for example, the radio station’s carrier frequency shifts its frequency more. In effect, FM translates changes in modulation amplitude into changes in carrier frequency. The modulation does not alter the level of the carrier wave. As a result, an FM signal electrically looks like a train of wide and narrow waves of constant height, as shown in Figure 8.4.
In a pure FM system, the strength or amplitude of the signal is irrelevant. This characteristic makes FM almost immune to noise. Interference and noise signals add into the desired signal and alter its strength, but FM demodulators ignore these amplitude changes. That’s why lightning storms and motors don’t interfere with FM radios. This same immunity from noise and variations in amplitude makes frequency modulation a more reliable, if more complex, transmission method for digital data.
Phase Modulation
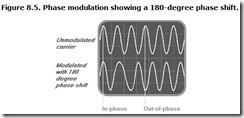
Another variation on the theme of frequency modulation is phase modulation. This technology works by altering the phase relationship between the waves in the signal. An unmodulated carrier is a train wave in a constant phase relationship. That is, the waves follow one after another precisely in step. The peaks and troughs of the train of waves flow in constant intervals. If one wave were delayed for exactly one wavelength, it would fit exactly atop the next one.
By delaying the peak of one wave so that it occurs later than it should, you can break the constant phase relationship between the waves in the train without altering the overall amplitude or frequency of the wave train. In other words, you shift the onset of a subsequent wave compared to those that precede it. At the same time, you will create a detectable state change called a phase shift. You can then code digital bits as the presence or absence of a phase shift.
Signals are said to be “in phase” when the peaks and troughs of one align exactly with another. When signals are 180 degrees “out of phase,” the peaks of one signal align with the troughs of the other. Figure 8.5 shows a 180-degree phase shift of a carrier wave. Note that the two waveforms shown start “in phase” and then, after a phase shift, end up being 180 degrees out of phase.
If you examine the shapes of waves that result from a phase shift, you’ll see that phase modulation is a special case of FM. Delaying a wave lengthens the time between its peak and that of the preceding wave. As a result, the frequency of the signal shifts downward during the change, although over the long term the frequency of the signal appears to remain constant.
One particular type of phase modulation. called quadrature modulation. alters the phase of the signal solely in increments of 90 degrees. That is, the shift between waves occurs at a phase angle of 0, 90, 180, or 270 degrees. The “quad” in the name of this modulation method refers to the four possible phase delays.
Pulse Modulation
Pulse modulation is actually a digital signal made up from discrete pulses of energy. The pulses have an underlying characteristic frequency—essentially their data clock—that is the equivalent of a carrier wave. In fact, to analog circuits, some forms of pulse modulation are demodulated as if they were analog signals. For example, add in some extra pulses, and you change the apparent frequency of the clock/carrier, thus creating frequency modulation. Change the duty cycle of the pulses (make the “on” part of the pulse last longer or shorter), and the analog strength of the carrier varies, thus creating analog modulation.
But you can also alter the pulses in a strictly digital manner, changing the bit-pattern to convey information. The signal then is completely digital, yet it still acts like it is an ordinary modulated carrier wave because it retains its periodic clock signal.
Pulse frequency modulation (PFM) is the simplest form of most pulse modulation. Using PFM, the modulator changes the number of pulses in a given period to indicate the strength of the underlying analog signal. More pulses means a higher frequency, so the frequency changes in correspondence with the amplitude of the analog signal. The result can be detected as ordinary frequency modulation.
Pulse width modulation (PWM) varies the width of each pulse to correspond to the strength of the underlying analog signal. This is just another way of saying that PWM alters the duty cycle of the pulses. The changes in signal strength with modulation translate into ordinary amplitude modulation.
Pulse code modulation (PCM) is the most complex form of pulse modulation, and it is purely digital. PCM uses a digital number or code to indicate the strength of the underlying analog signal. For example, the voltage of the signal is translated into a number, and the digital signal represents that number in binary code. This form of digital modulation is familiar from its wide application in digital audio equipment such as CD players.
Pulse position modulation (PPM) uses the temporal position of a pulse within a clock period to indicate a discrete value. For example, the length of one clock period may be divided into four equal segments. A pulse can occur in one, and only one, of these chip segments, and which chip the pulse appears in (its position inside the symbol duration or clock period) encodes its value. For example, the four segments may be numbered 0, 1, 2, and 3. If the pulse appears in segment 2, that clock period carries a value of 2.
Figure 8.6 shows the pulse position for the four valid code values using the PPM scheme developed for the IrDA interface.
Complex Modulation
The various modulation techniques are not mutually exclusive. Engineers have found ways of pushing more data through a given communication channel by combining two or more techniques to create complex modulation schemes.
In broadcasting, complex modulation is not widely used. There’s not much point to it. In data communications, however, it allows engineers to develop systems in which a signal can have any of several states in a clock period. Each state, called a symbol by engineers, can encode one or more bits of data. The more states, the more bits that each symbol can encode using a technique called group-coding, which is discussed later in the section with the same name.
Parallel Channels
A parallel connection is one with multiple signals traveling down separate wires, side by side. For computers, this is the natural way of dealing with communications. Everything about a microprocessor is parallel. Its registers look at data bits in parallel—32 or more at a time. The chip sucks information into its circuitry the same way—32, 64, or even 128 bits at a time. It’s only natural. The chip works on multiple bits with every tick of the system clock, so you want to fill it with data the same way (and at the same rate).
When it comes time for the chip to communicate—both with the rest of the computer and with the outside world—it’s only natural to use the same kind of connection, one that can pass multiple data bits in parallel. Moreover, by providing a number of data paths, a parallel channel has the potential for moving more information in a given time. Parallel channels can be faster.
With this design philosophy in mind, engineers have developed parallel communication channels of two types. Expansion buses provide a wide, parallel path for data inside the computer. The familiar Peripheral Component Interconnect (PCI) bus is such a design. Parallel communications ports serve to connect the computer with other equipment. The parallel printer port is the exemplar of this technology.
Of the two, ports are simpler. They just have less to do. They connect external devices to the computer, and they only need to move information back and forth. They sacrifice the last bit of versatility for practicality. Expansion buses must do more. In addition to providing a route for a stream of data, they also must provide random access to that data. They must operate at higher speeds, as well, as close to the clock speed of the microprocessor as can be successfully engineered and operated. They need more signals and a more complex design to carry out all their functions.
Some designs, however, straddle the difference. SCSI offers external parallel connections like a port but also works a bit like an expansion bus. The common hard disk interface, AT Attachment (or IDE), is part of an expansion bus, but it doesn’t allow direct addressing. All, however, use parallel channels to move their information.
Ports
The concept behind a parallel port is simply to extend the signals of the computer to another device. When microprocessors had data buses only eight bits wide, providing an external connection with the same number of bits was the logical thing to do. Of course, when microprocessors had data buses only eight bits wide, the circuitry needed in order to convert signals to another form was prohibitively expensive, especially when you need to convert the signal when it leaves the computer and convert it back to parallel form at the receiving device, even a device as simple as a printer. Of course, when microprocessors had eight-bit data buses, Mammoths still strode the earth (or so it seems).
Many people use the term port to refer to external connections on their computers. A port is a jack into which you plug a cable. By extension, the name refers to the connection system (and standard) used to make the port work. Take a similar design and restrict it to use inside the computer, and it becomes an interface, such as the common disk interfaces. By these definitions, the Small Computer System Interface (SCSI) is schizophrenic. It has a split personality and works either way. In truth, the terms port and interface have many overlapping meanings.
In the modern world, parallel connections have fallen by the wayside for use as ports. One reason is that it has become cheaper to design circuits to convert signal formats. In addition, the cost of equipping signal paths to ward off interference increases with every added path, so cables for high-speed parallel connections become prohibitively expensive. Consequently, most new port designs use serial rather than parallel technology. But parallel designs remain a good starting point in any discussion of communications because they are inherently simpler, working with computer data in its native form.
Even the most basic parallel connection raises several design issues. Just having a parallel connection is not sufficient. Besides moving data from point to point, a parallel channel must be able to control the flow of data, both pacing the flow of bits and ensuring that information won’t be dumped where it cannot be used. These issues will arise in the design of every communications system.
Data Lines
The connections that carry data across a parallel channel are termed data lines. They are nothing more than wires that conduct electrical signals from one end of the connection to the other. In most parallel channels, the data lines carry ordinary digital signals, on-or-off pulses, without modulation.
The fundamental factor in describing a parallel connection is therefore the number of data lines it provides. More is always better, but more also means increased complexity and cost. As a practical matter, most parallel channels use eight data lines. More usually is unwieldy, and fewer would be pointless. The only standard connection system to use more than eight is Wide SCSI, which doubles the channel width to 16 bits to correspondingly double its speed potential.
Although today’s most popular standards use only enough data lines to convey data, sometimes engineers add an extra line for each eight called a parity-check line. Parity-checking provides a means to detect errors that might occur during communication.
Parity-checking uses a simple algorithm for finding errors. The sending equipment adds together the bits on the data lines without regard to their significance. That is, it checks which lines carry a digital one (1) and which carry a digital zero (0). It adds all the ones together. If the sum is an odd number, it makes the parity-check line a one. If the sum is even, it makes the parity-check line a zero. In that way, the sum of all the lines—data lines and parity-check lines—is always an even number. The receiving equipment repeats the summing. If it comes up with an odd number, it knows the value of one of the data lines (or the parity-check line) has changed, indicating an error has occurred.
Timing
The signals on a parallel channel use the same clocked logic as the signals inside a computer. Accordingly, there are times when the signals on the data lines are not valid—for example, when they are changing or have changed but are not yet stable. As with the signals inside the computer system, the parallel channel uses a clock to indicate when the signals on the data lines represent valid data and when they do not.
The expedient design, in keeping with the rest of the design of the parallel channel, is to include an extra signal (and a wire to carry it) that provides the necessary clock pulses. Most parallel channels use a dedicated clock line to carry the pulses of the required timing signal.
Flow Control
The metaphor often used for a communications channel is that of a pipe. With nothing more to the design than data lines and a clock, that pipe would be open ended, like a waterline with the spigot stuck on. Data would gush out of it until the equipment drowned in a sea of bits. Left too long, a whole room might fill up with errant data; perhaps buildings would explode and scatter bits all over creation.
To prevent that kind of disaster, a parallel channel needs some means of moderating the flow of data, a giant hand to operate a digital spigot. With a parallel connection, the natural means of controlling data flow is yet another signal.
Some parallel channels have several such flow-control signals. In a two-way communications system, both ends of the connection may need to signal when they can no longer accept data. Additional flow-control signals might indicate specific reasons why no more data can be accepted. For example, one line in a parallel port might signal that the printer has run out of paper.
Buses
The computer expansion bus shows digital communications at its most basic—if you want to move digital signals away from a microprocessor, just make the wires longer. The first expansion bus shows this principle in action. The IBM Personal Computer expansion bus, which evolved into the Industry Standard Architecture (a defining characteristic of personal computers for nearly 15 years), was really nothing more than the connections to the microprocessor extended to reach further inside the computer.
Modern expansion buses go further—in technology rather than distance. Although they still stay within the confines of a computer’s case, they have evolved into elaborate switching and control systems to help move data faster. One of the reasons for this change in design arises from limitations imposed by the communications channel of the bus itself. In addition, the modern bus has evolved as a communications system independent of the microprocessor in the computer. By looking at the bus as a communications system unto itself, engineers have added both versatility and speed. The next generation of expansion buses will be almost indistinguishable from long-distance data communications systems, sharing nearly all their technologies, except for being shorter and faster.
Background
The concept of a bus is simple: If you have to move more information than a single wire can hold, use several. A bus is comprised of several electrical connections linking circuits carrying related signals in parallel. The similarity in the name with the vehicle that carries passengers across and between cities is hardly coincidental. Just as many riders fit in one vehicle, the bus, many signals travel together in an electrical bus. As with a highway bus, an electrical bus often makes multiple stops on its way to its destination. Because all the signals on a bus are related, a bus comprises a single communication channel.
The most familiar bus in computer systems is the expansion bus. As the name implies, it is an electrical bus that gives you a way to expand the potential of your computer by attaching additional electrical devices to it. The additional devices are often termed peripherals or, because many people prefer to reserve that term for external accessories, simply expansion boards.
A simple bus links circuits, but today’s expansion bus is complicated by many issues. Each expansion bus design represents a complex set of design choices confined by practical constraints. Designers make many of the choices by necessity; others they pick pragmatically. The evolution of the modern expansion bus has been mostly a matter of building upon the ideas that came before (or stealing the best ideas of the predecessors). The result in today’s computers is a high-performance Peripheral Component Interconnect, or PCI, upgrade system that minimizes (but has yet to eliminate) setup woes.
The range of bus functions and resources is wide. The most important of these is providing a data pathway that links the various components of your computer together. It must provide both the channel through which the data moves and a means of ensuring the data gets where it is meant to go. In addition, the expansion bus must provide special signals to synchronize the thoughts of the add-in circuitry with those of the rest of the computer. Newer bus designs (for example, PCI, but not the old Industry Standard Architecture, or ISA, of the last generation of personal computers) also include a means of delegating system control to add-in products and tricks for squeezing extra speed from data transfers.
Although not part of the electrical operation of the expansion bus, the physical dimensions of the boards and other components are also governed by agreed-on expansion bus specifications, which we will look at in Chapter 30, “Expansion Boards.” Moreover, today’s bus standards go far beyond merely specifying signals. They also dictate transfer protocols and integrated, often automated, configuration systems.
How these various bus features work—and how well they work—depends on the specific features of each bus design. In turn, the expansion bus design exerts a major influence on the overall performance of the computer it serves. Bus characteristics also determine what you can add to your computer—how many expansion boards, how much memory, and what other system components—as well as how easy your system is to set up. The following sections examine the features and functions of all expansion buses, the differences among them, and the effects of those differences in the performance and expandability of your computer.
Data Lines
Although the information could be transferred inside a computer either by serial or parallel means, the expansion buses inside computers use parallel data transfers. The choice of the parallel design is a natural. All commercial microprocessors have parallel connections for their data transfers. The reason for this choice in microprocessors and buses is exactly the same: Parallel transfers are faster. Having multiple connections means that the system can move multiple bits every clock cycle. The more bits the bus can pass in a single cycle, the faster it will move information. Wider buses—those with more parallel connections—are faster, all else being equal.
Ideally, the expansion bus should provide a data path that matches that of the microprocessor. That way, an entire digital quad-word used by today’s Pentium-class microprocessors (a full 64 bits) can stream across the bus without the need for data conversions. When the bus is narrower than a device that sends or receives the signals, the data must be repackaged for transmission—the computer might have to break a quad-word into four sequential words or eight bytes to fit an old 16- or 8-bit bus. Besides the obvious penalty of requiring multiple bus cycles to move the data the microprocessor needs, a narrow bus also makes system design more complex. Circuitry to handle the required data repackaging complicates both motherboards and expansion boards.
On the other hand, increasing the number of data connections also complicates the design of a computer, if just because of the extra space and materials required. Finding the optimal number of connections for a given application consequently is a tradeoff between speed (which requires more connections) and complexity (which increases with connection count and thus speed).
In modern computers with multiple expansion buses, each bus usually has a different number of data connections, reflecting the speed requirements of each bus. The bus with the highest performance demands—the memory bus—has the most connections. The bus with the least performance demands—the compatibility bus—has the fewest.
Address Lines
As long as a program knows what to do with data, a bus can transfer information without reference to memory addresses. Having address information available, however, increases the flexibility of the bus. For example, making addressing available on the bus enables you to add normal system memory on expansion boards. Addressing allows memory-mapped information transfers and random access to information. It allows data bytes to be routed to the exact location at which they will be used or stored. Imagine the delight of the dead letter office of the Post Office and the ever-increasing stack of stationery accumulating there if everyone decided that appending addresses to envelopes was superfluous. Similarly, expansion boards must be able to address origins and destinations for data. The easiest method of doing this is to provide address lines on the expansion bus corresponding to those of the microprocessor.
The number of address lines used by a bus determines the maximum memory range addressable by the bus. It’s a purely digital issue—two to the power of the number of address lines yields the maximum discrete address values that the bus can indicate. A bus with eight address lines can address 256 locations (two to the eighth power); with 16 address lines, it can identify 65,536 locations (that is, two to the sixteenth power.)
Engineers have a few tricks to trim the number of address lines they need. For example, modern microprocessors have no need to address every individual byte. They swallow data in 32- or 64-bit chunks (that is, double-words or quad-words). They do not have to be able to address memory any more specifically than every fourth or eighth byte. When they do need to retrieve a single byte, they just grab a whole double-word or quad-word at once and sort out what they need internally. Consequently, most 32-bit expansion buses designed to accommodate these chips commonly delete the two least-significant address bits.
Some bus designs eliminate the need for address lines entirely by using multiplexing. Instead of separate address lines for addresses and data, they combine the functions on the same connections. Some multiplexed designs use a special signal that, when present, indicates the bits appearing on the combined address and data lines are data. In the absence of the signal, the bits on the lines represent an address. The system alternates between addresses and data, first giving the location to put information and then sending the information itself. In wide-bus systems, this multiplexing technique can drastically cut the number of connections required. A full 64-bit system might have 64 address lines and 64 data lines—a total of 128 connections for moving information. When multiplexed, the same system could get by with 65 connections—64 combined address/data lines and one signal to discriminate which is which.
Most systems require an address for every transfer of data across the bus. That is, for each 32-bit transfer through a 32-bit bus, the system requires an address to indicate where that information goes. Some buses allow for a burst mode, in which a block of data going to sequential addresses travels without indicating each address. Typically, a burst-mode transfer requires a starting address, the transfer of data words one after another, and some indication the burst has ended. A burst mode can nearly double the speed of data transfer across the bus.
Timing
Buses need timing or clock signals for two reasons. The bus may be called upon to distribute timing systems throughout a computer to keep all the circuits synchronized. In addition, the data traveling on the bus itself requires clocking—the clock signal indicates when the data (or addresses, or both) on the bus is valid.
The same signal can be used for clocking the bus data and synchronizing other circuits. Such a bus is termed synchronous because it is synchronized. Alternatively, the bus may have two (or more) separate clock signals for different purposes. Buses in which the clock for data on the bus is not synchronized with the system clock are termed asynchronous buses.
Flow Control
Buses require flow control for the same reason as ports—to prevent peripherals from being swamped with a tidal wave of data or to keep a peripheral from flooding the rest of the system. To avoid data losses when a speed disparity arises between peripherals and the host, most buses include flow-control signals. In the simplest form, the peripheral sends a special “not ready” signal across the bus, warning the host to wait until the peripheral catches up. Switching off the “not ready” signal indicates to the host to dump more data on the peripheral.
System Control
Buses often carry signals for purposes other than moving data. For example, computer expansion buses may carry separate lines to indicate each interrupt or request for a DMA transfer. Alternatively, buses can use signals like those of parallel ports to indicate system faults or warnings.
Most buses have a reset signal that tells the peripherals to initialize themselves and reset their circuits to the same state they would have when initially powering up. Buses may also have special signals that indicate the number of data lines containing valid data during a transfer. Another signal may indicate whether the address lines hold a memory address or an I/O port address.
Bus-Mastering
In the early days of computers, the entire operation of the expansion bus was controlled by the microprocessor in the host computer. The bus was directly connected to the microprocessor; in fact, the bus was little more than an extension of the connections on the chip itself. A bus connected directly to the microprocessor data and address lines is termed a local bus because it is meant to service only the components in the close vicinity of the microprocessor itself. Most modern buses now use a separate bus controller that manages the transfers across the bus.
Many bus designs allow for decentralized control, where any device connected to the bus (or any device in a particular class of devices) may take command. This design allows each device to manage its own transfers, thus eliminating any bottlenecks that can occur with a single, centralized controller. The device that takes control of the bus is usually termed a bus master. The device that it transfers data to is the bus slave. The bus master is dynamic. Almost any device may be in control of the bus at any given moment. Only the device in control is the master of the bus. However, in some systems where not every device can control the bus, the devices that are capable of mastering the bus are termed “bus masters,” even when they are not in control—or even installed on the system, for that matter.
If multiple devices try to take control of the bus at the same time, the result is confusion (or worse, a loss of data). All buses that allow mastering consequently must have some scheme that determines when and which master can take control of the bus, a process called bus arbitration. Each bus design uses its own protocol for controlling the arbitration process. This protocol can be software, typically using a set of commands set across the bus like data, or hardware, using special dedicated control lines in the bus. Most practical bus designs use a hardware signaling scheme.
In the typical hardware-based arbitration system, a potential master indicates its need to take control of the bus by sending an attention signal on a special bus line. If several devices want to take control at the same time, an algorithm determines which competing master is granted control, how long that control persists, and when after losing control it can be granted the same master again.
In software-based systems, the potential bus master device sends a request to its host’s bus-control logic. The host grants control by sending a special software command in return.
The design of the arbitration system usually has two competing goals: fairness and priority. Fairness ensures that one device cannot monopolize the bus, and that within a given period every device is given a crack at bus control. For example, some designs require that once a master has gotten control of the bus, it will not get a grant of control again until all other masters also seeking control have been served. Priority allows the system to act somewhat unfairly, to give more of the bus to devices that need it more. Some bus designs forever fix the priorities of certain devices; others allow priorities of some or all masters to be programmed.
Power Distribution
Although all electrical devices need some source of electricity to operate, no immutable law requires an expansion bus to provide that power. For example, when you plug a printer into your computer, you also usually plug the printer into a wall outlet. Similarly, peripherals could have their own sources of needed electricity. Providing that power on the bus makes the lives of engineers much easier. They don’t have to worry about the design requirements, metaphysics, or costs of adding power sources such as solar panels, magnetohydrodynamic generators, or cold fusion reactors to their products.
Non-Bussed Signals
Buses are so named because their signals are “bused” together; but sometimes engineers design buses with separate, dedicated signals to individual devices. Most systems use only a single device-specific signal on a dedicated pin (the same pin at each device location, but a different device-specific signal on the pin for each peripheral). This device-specific signaling is used chiefly during power-on testing and setup. By activating this signal, one device can be singled out for individual control. For example, in computer expansion buses, a single, non-bussed signal allows each peripheral to be individually activated for testing, and the peripheral (or its separately controllable parts) can be switched off if defective. Device-specific signals also are used to poll peripherals individually about their resource usage so that port and memory conflicts can be automatically managed by the host system.
Bridges
The modern computer with multiple buses—often operating with different widths and speeds—poses a problem for the system designer: how to link those buses together. Make a poor link-up, and performance will suffer on all the buses.
A device that connects two buses together is called a bridge. The bridge takes care of all the details of the transfer, converting data formats and protocols automatically without the need for special programming or additional hardware.
A bridge can span buses that are similar or different. A PCI-based computer can readily incorporate any bus for which bridge hardware is available. For example, in a typical PCI system, bridges will link three dissimilar buses—the microprocessor bus, the high-speed PCI bus, and an ISA compatibility bus—and may additionally tie in another, similar PCI bus to yield a greater number of expansion opportunities.
The interconnected buses logically link together in the form of a family tree, spreading out as it radiates downward. The buses closer to the single original bus at the top are termed upstream. Those in the lower generations more distant from the progenitor bus are termed downstream. Bridge design allows data to flow from any location on the family tree to any other. However, because each bridge imposes a delay for its internal processing, called latency, a transfer that must pass across many bridges suffers performance penalties. The penalties increase the farther downstream the bus is located.
To avoid latency problems, when computers have multiple PCI buses, they are usually arranged in a peer bus configuration. That is, instead of one bridge being connected to another, the two or three bridges powering the expansion buses in the computer are connected to a common point—either the PCI controller or the most upstream bridge.
Serial Channels
The one great strength of a bus—its wealth of signal pathways—can be its greatest disadvantage. For every digital signal you want to move, you’ve got to arrange for 8, 16, even 64 separate connections, and each one must be protected from interference. Simple cables become wide, complex, and expensive. Plugs and jacks sprout connections like a Tyrannosaurus Rex’s mouth does teeth—and can be just as vicious. You also need to work out every day at the gym just to plug one in. Moreover, most communications channels provide a single data path, much a matter of history as convenience. For conventional communications such as the telephone, a single pathway (a single pair of wires) suffices for each channel.
The simplicity of a single data pathway has another allure for engineers. It’s easier for them to design a channel with a single pathway for high speeds than it is to design a channel with multiple pathways. In terms of the amount of information they can squeeze through a channel, a single fast pathway can move more information than multiple slower paths.
The problem faced by engineers is how to convert a bus signal into one compatible with a single pathway (say, a telephone connection). As with most communications problems, the issue is one of coding information. A parallel connection like a bus encodes information as the pattern of signals on the bus when the clock cycles. Information is a snapshot of the bits on the bus, a pattern stretched across space at one instant of time. The bits form a line in physical space—a row of digital ones and zeroes.
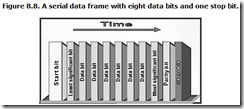
The solution is simple: Reverse the dimensions. Let the data stretch out into a long row, not in the physical dimension but instead across time. Instead of the code being a pattern that stretches across space, it becomes a code that spans time. Instead of the parallel position of the digital bits coding the information, their serial order in a time sequence codes the data. This earns its name “serial” because the individual bits of information are transferred in a long series. Encoding and moving information in which the position of bits in time conveys importance is called serial technology, and the pathway is a called a serial channel.
Clocking
The most straightforward way of communicating (or storing) data is to assign a digital code so that the presence of a signal (for instance, turning on a five-volt signal) indicates a digital value of one, and another signal (say, zero volts) indicates the other digital value, zero. That’s what digital is all about, after all.
However, such a signaling system doesn’t work very well to communicate or store digital values, especially when the values are arranged in a serial string. The problem is timing. With serial data, timing is important in sorting out bits, and a straight one-for-one coding system doesn’t help with timing.
The problem becomes apparent when you string a dozen or so bits of the same value in a row. Electrically, such a signal looks like a prolonged period of high or low voltage, depending on whether the signal is a digital one or zero. Some circuit has to sort out how many bits on one value this prolonged voltage shift represents. If the “prolonged” voltage lasts only a bit or two, figuring out how many bits is pretty easy. The length of a two-bit string differs from a three-bit string by 50 percent. If you time the duration of the shift, the accuracy of your timing needs only to be accurate to a bit less than 50 percent for you to properly sort out the bits. But string 100 bits in a row, and a mistake of 2 percent in timing can mean the loss or, worse, misinterpretation of two bits of information.
An easy way to sort out the bits is to provide a separate timing signal, a clock, that defines when each bit begins and ends. A separate clock is standard operating procedure for clocked logic circuits, anyway. That’s why they are called clock logic. You can similarly provide a clock signal in communication circuits. Just add a separate clock signal.
However, a separate clock would take a separate channel, another communication circuit, with all its added complication. Consequently, engineers have developed ways of eliminating the need for a separate clock.
Synchronous communications require the sending and receiving system—for our purposes, the computer and printer—to synchronize their actions. They share a common timebase, a serial clock. This clock signal is passed between the two systems either as a separate signal or by using the pulses of data in the data stream to define it. The serial transmitter and receiver can unambiguously identify each bit in the data stream by its relationship to the shared clock. Because each uses exactly the same clock, they can make the match based on timing alone.
In asynchronous communications, the transmitter and receiver use separate clocks. Although the two clocks are supposed to be running at the same speed, they don’t necessarily tell the same time. They are like your wristwatch and the clock on the town square. One or the other may be a few minutes faster, even though both operate at essentially the same speed: a day has 24 hours for both.
An asynchronous communications system also relies on the timing of pulses to define the digital code. But they cannot look to their clocks as infallible guidance. A small error in timing can shift a bit a few positions (say, from the least-significant place to the most significant), which can drastically affect the meaning of the digital message.
If you’ve ever had a clock that kept bad time—for example, the CMOS clock inside your computer—you probably noticed that time errors are cumulative. They add up. If your clock is a minute off today, it will be two minutes off tomorrow. The more time that elapses, the more the difference between two clocks will be apparent. The corollary is also true: If you make a comparison over a short enough period, you won’t notice a shift between two clocks even if they are running at quite different speeds.
Asynchronous communications banks on this fine slicing of time. By keeping intervals short, they can make two unsynchronized clocks act as if they were synchronized. The otherwise unsynchronized signals can identify the time relationships in the bits of a serial code.
Isochronous communications involve time-critical data. Your computer uses information that is transferred isochronously in real time. That is, the data is meant for immediate display, typically in a continuous stream. The most common examples are video image data that must be displayed at the proper rate for smooth full-motion video and digital audio data that produces sound. Isochronous transmissions may be made using any signaling scheme—be it synchronous or asynchronous. They usually differ from ordinary data transfers in that the system tolerates data errors. It compromises accuracy for the proper timing of information. Whereas error-correction in a conventional data transfer may require the retransmission of packets containing errors, an isochronous transmission lets the errors pass through uncorrected. The underlying philosophy is that a bad pixel in an image is less objectionable than image frames that jerk because the flow of the data stream stops for the retransmission of bad packets.
Bit-Coding
In putting bits on a data line, a simple question arises: What is a bit, anyway? Sure, we know what of bit of information is—it’s the smallest possible piece of information. However, in a communications system, the issue is what represents each bit. It could be a pulse of electricity, but it could equally be a piece of copper in the wire or a wildebeest or a green-and-purple flying saucer with twin chrome air horns. Although some of these codes might not be practical, they would be interesting.
Certainly the code will have to be an electrical signal of some sort. After all, that’s what we can move through wires. But what’s a bit? What makes a digital one and what makes a digital zero?
The obvious thing to do is make the two states of the voltage on the communication wire correspond to the two digital states. In that way, the system signals a digital one as the presence of a voltage and a zero as its absence.
To fit with the requirements of a serial data stream, each bit gets assigned a timed position in the data stream called a bit-cell. In most basic form, if a bit appears in the cell, it indicates a digital one; if not, it’s a zero.
Easy enough. But such a design is prone to problems. A long string of digital ones would result in a constant voltage. In asynchronous systems, that’s a problem because equipment can easily lose track of individual bits. For example, when two “ones” travel one after another, the clock only needs to be accurate to 50 percent of the bit-length to properly decipher both. With a hundred “ones” in a series, even a 1 percent inaccuracy will lose a bit or more of data.
RTZ
To help keep the data properly clocked, most digital signals work by switching each bit both on and off in each bit-cell. To indicate a digital one, the most basic of such systems will switch on a voltage and then switch it off before the end of the bit-cell. Because the signaling voltage rises and then falls back to zero in each data cell, this form of bit-coding is called Return-to-Zero coding, abbreviated RTZ.
RZI
Related to RTZ is Return-to-Zero Inverted coding, abbreviated RZI. The only difference is a result of the I in the designation, the inversion, which simply means that a pulse of electricity encodes a digital zero instead of a digital one. The voltage on the line is constant except when interrupted by a pulse of data.
NRZ
Although RTZ and RZI bit-coding are simple, they are not efficient. They effectively double the frequency of the data signal, thus increasing the required bandwidth for a given rate of data transmission by a factor of two. That’s plain wasteful.
Engineers found a better way. Instead of encoding bits as a voltage level, they opted to code data as the change in voltage. When a bit appears in the data stream, NRZ coding shifts the voltage from whatever it is to its opposite. A bit could be a transition from zero to high voltage or the transition back the other way, from high voltage to zero. The signal then remains at that level until the next bit comes along. Because each bit does not cause the signal to fall back to zero voltage, this system is called No Return-to-Zero bit-coding.
NRZI
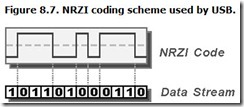
A related form of signaling is No Return-to-Zero Inverted bit-coding. The inversion is before the coding. That is, a lack of a data bit in a bit-cell causes the coded signal voltage to change. If data appears in the bit-cell, no change occurs in the encoded signal. Note that a zero in the code stream triggers each transition in the resulting NRZI code. A long period of no data on an NRZI-encoded channel (a continuous stream of logical zeros) results in a on-off pattern of voltages on the signal wires. This signal is essentially a square wave, which looks exactly like a clock signal. Figure 8.7 shows how the transitions in an NRZI signal encode data bits.
The NRZI signal is useful because it is self-clocking. That is, it allows the receiving system to regenerate the clock directly from the signal. For example, the square wave of a stream of zeros acts as the clock signal. The receiver adjusts its timing to fit this interval. It keeps timing even when a logical one in the signal results in no transition. When a new transition occurs, the timer resets itself, making whatever small adjustment might be necessary to compensate for timing differences at the sending and receiving ends.
Bit-Stuffing
No matter the coding scheme, including NRZI, long periods of an unchanging signal can still occur. With an NRZ signal, a string of zeros results in no signal. In NRZI, it takes a string of digital ones, but it can happen nevertheless. And if it does, the result can be clock problems and data errors.
For example, two back-to-back bit-cells of constant voltage can be properly decoded even if the data clock is 50 percent off. But with 100 back-to-back data cells of constant voltage, even being 1 percent off will result in an error. It all depends on the data.
That’s not a good situation to be in. Sometimes the data you are sending will automatically cause errors. An engineer designing such a system might as well hang up his hat and jump from the locomotive.
But engineers are more clever than that. They have developed a novel way to cope with any signal and ensure that constant voltage will never occur: break up the stream of data that causes the uninterrupted voltage by adding extra bits that can be stripped out of the signal later. Adding these removable extraneous bits results in a technology called bit-stuffing.
Bit-stuffing can use any of a variety of algorithms to add extra bits. For example, bit-stuffing as used by the Universal Serial Port standard injects a zero after every continuous stream of six logical ones. Consequently, a transition is guaranteed to occur at least every seven clock cycles. When the receiver in a USB system detects a lack of transitions for six cycles and then receives the transition of the seventh, it knows it has received a stuffed bit. It resets its timer and discards the stuffed bit and then counts the voltage transition (or lack of it) occurring at the next clock cycle to be the next data bit.
Group-Coding
Bit-coding is a true cipher in that it uses one symbol to code another—a bit of data is one symbol, and the voltage on the communication line (or its change) is a different one. Nothing about enciphering says, however, that one bit must equal one symbol. In fact, encoding groups of bits as individual symbols is not only possible but also often a better strategy. For obvious reasons, this technology is called group-coding.
Can’t think of a situation where one symbol equals multiple bits would work? Think about the alphabet. The ASCII code—ASCII is short for the American Standard Code for Information Interchange—that’s used for encoding letters of the alphabet in binary form is exactly that. The letter H, for example, corresponds to the binary code 00101000 in ASCII.
Certain properties of data communications systems and data storage systems make group-coding the most efficient way of moving and storing information. Group-coding can increase the speed of a communications system, and it can increase the capacity of a storage system.
One way that group-coding can increase data communication speed is when the communications medium allows you to use more than the two binary states to encode bits. For example, if a telephone line is stable, predictable, and reliable enough, you might be able to distinguish four different voltage levels on the line instead of just two (on and off). You could use the four states each as an individual symbol to encode bit-patterns. This example allows for an easy code in which numbers encode the binary value, as shown in Table 8.1.
Although this encoding process seems trivial, it actually doubles the speed of the communication channel. Send the symbols down the line at the highest speed it allows. When you decode the symbols, you get twice as many bits. This kind of group-coding makes high-speed modems possible.
In the language of telecommunications, the speed at which symbols move through a communications medium is measured in units of baud. One baud is a communications rate of one symbol per second. The term baud was named after J.M.E. Baudot, a French telegraphy expert. His full name (Baudot) is used to describe a five-bit digital code used in teletype systems.
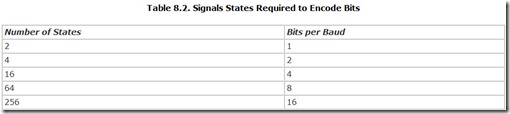
The relationship between the number of bits that can be coded for each baud and the number of signal symbols required is geometric. The number of required symbols skyrockets as you try to code more data in every baud, as shown in Table 8.2.
Although it can be more efficient, this form of group-coding has a big disadvantage. It makes the transmitted data more vulnerable to error. An error in one bad baud causes multiple bits of raw data to be wrong. Moreover, the more symbols you use in any communication medium, the more similar they are to one another. The smaller the differences between symbols, the more likely errors will result from smaller disruptions to the signal. With modems, this drawback translates into the need for the best possible connection.
Engineers use a similar group-coding technique when they want to optimize the storage capacity of a medium. As with communications systems, storage systems suffer bandwidth limitations. The electronics of a rotating storage system such as a hard disk drive (see Chapter 17, “Magnetic Storage”) are tuned to operate at a particular frequency, which is set by the speed the disk spins and how tightly bits can be packed on the disk. The packing of bits is a physical characteristic of the storage medium, which is made from particles of a finite size. Instead of electrical signals, hard disks use magnetic fields to encode information. More specifically, the basic storage unit is the flux transition, the change in direction of the magnetic field. Flux transitions occur only between particles (or agglomerations of particles). A medium can store no more data than the number of flux transitions its magnetic particles can make.
The first disk systems recorded a series of regularly spaced flux transitions to form a clock. An extra flux transition between two clock bits indicated a one in digital data. No added flux transition between bits indicated a zero. This system essentially imposed an NRZ signal on the clock and was called frequency modulation because it detected data as the change in frequency of the flux transitions. It was also called single-density recording.
The FM system wastes half of the flux transitions on the disk because of the need for the clock signal. By eliminating the clock and using a coding system even more like NRZ, disk capacities could be doubled. This technique, called Modified Frequency Modulation recording (MFM) or double-density recording was once the most widely used coding system for computer hard disks and is still used by many computer floppy disk drives. Instead of clock bits, digital ones are stored as a flux transition and zeros as the lack of a transition within a given period. To prevent flux reversals from occurring too far apart, MFM differs from pure NRZ coding by adding an extra flux reversal between consecutive zeros.
Modern disks use a variety of group-codings called Run Length Limited (RLL). The symbols used for coding data in RLL are bit-patterns, but patterns that are different from the data to be recorded. The RLL patterns actually use more bits than the original data. RLL increases data density by the careful choice of which bit-patterns to use.
RLL works by using a flux transition to indicate not individual bits but the change from zero to one or from one to zero. If two ones occur in a row, there’s no flux transition. If eight ones occur in a row, there is still no flux transition. Similarly, two or eight zeros in a row result in no flux transition. The trick in RLL is to choose bit-patterns that only have long series of ones or zeros in them, resulting in fewer flux transitions.
The first common RLL system was called 2,7 RLL because it used a set of symbols, each 16-bits long, chosen so that no symbol in the code had fewer than two identical bits and more than seven. Of the 65,564 possible 16-bit symbols, the 256 with the bit-patterns best fitting the 2,7 RLL requirements encode the 256 possible byte values of the original data. In other words, the RLL coding system picks only the bit-patterns that allow the highest storage density from a wide-ranging group of potential symbols. The 16-bit code patterns that do not enforce the 2,7 rule are made illegal and never appear in the data stream that goes to the magnetic storage device. Although each symbol involves twice as many bits as the original data, the flux transitions used by the code occur closer together, resulting in a 50 percent increase in the capacity of the storage system.
Other RLL systems, sometimes called Advanced RLL, work the same way but use different code symbols. One system uses a different code that changes the bit-pattern so that the number of sequential zeros is between three and nine. This system, known for obvious reasons as 3,9 RLL or Advanced RLL, still uses an 8-to-16 bit code translation, but it ensures that digital ones will never be closer than every four bits. As a result, it allows data to be packed into flux transitions four times denser. The net gain is that information can be stored about twice as densely with 3,9 RLL as ordinary double-density recording techniques.
Frames
The basic element of digital information in a serial communications system is the data frame. Think of this as a time frame, the frame bracketing the information like a frame surrounds a window. The bits of the digital code are assigned their value in accord with their position in the frame. In a synchronous serial communications system, the frame contains the bits of a digital code word. In asynchronous serial communications, the frame also contains a word of data, but it has a greater significance. It is also the time interval in which the clocks of the sending and receiving systems are assumed to be synchronized.
When an asynchronous receiver detects the start of a frame, it resets its clock and then uses its clock to define the significance of each bit in the digital code within the frame. At the start of the next frame, it resets its clock and starts timing the bits again.
The only problem with this system is that an asynchronous receiver needs to know when a frame begins and ends. Synchronous receivers can always look to the clock to know, but the asynchronous system has no such luxury. The trick to making asynchronous communications work is unambiguously defining the frame. Today’s asynchronous systems use start bits to mark the beginning of a frame and stop bits to mark its end. In the middle are a group of data bits.
The start bit helps the asynchronous receiver find data in a sea of noise. In some systems, the start bit is given a special identity. In most asynchronous systems, it is twice the length of the other bits inside the frame. In others, the appearance of the bit itself is sufficient. After all, without data, you would expect no pulses. When any pulse pops up, you might expect it to be a start bit.
Each frame ends with one or more stop bits. They assure the receiver that the data in the frame is complete. Most asynchronous communication systems allow for one, one and a half, or two stop bits. Most systems use one because that length makes each frame shorter (which, in turn, means that it takes a shorter time to transmit).
The number of data bits in a frame varies widely. In most asynchronous systems, there will be from five to eight bits of data in each frame. If you plan to use a serial port to connect a modern serial device to your computer, your choices will usually be to use either seven bits or eight bits, the latter being the most popular.
In addition, the data bits in the frame may be augmented by error-correction information called a parity bit, which fits between the last bit of data and the stop bit. In modern serial systems, any of five varieties of parity bits are sometimes used: odd, even, space, mark, and none.
The value of the parity bit is keyed to the data bits. The serial transmitter counts the number of digital ones in the data bits and determines whether this total is odd or even. In the odd parity scheme, the transmitter will turn on the parity bit (making it a digital one) only if the total number of digital ones in the data bits is odd. In even priority systems, the parity bit is set as one only if the data bits contain an even number of digital ones. In mark parity, the parity bit is always a mark, a digital one. In space parity, the parity bit is always a space, a digital zero. With no parity, no parity bit is included in the digital frames, and the stop bits immediately follow the data bits.
By convention, the bits of serial data in each frame are sent least-significant bit first. Subsequent bits follow in order of increasing significance. Figure 8.8 illustrates the contents of a single data frame that uses eight data bits and a single stop bit.
A frame corresponds to a single character. Taken alone, that’s not a whole lot of information. A single character rarely suffices for anything except answering multiple-choice tests. To make something meaningful, you combine a sequence of characters together to form words and sentences.
The serial communications equivalent of a sentence is a packet. A packet is a standardized group of characters, or frame, that makes up the smallest unit that conveys information through the communications system.
As the name implies, a packet is a container for a message, such as a diplomatic packet or envelope. The packet holds the data. In addition, in most packetized systems, the packet also includes an address and, often, a description of its contents. Packets may also include extra data to ensure the integrity of their contents (for example, an error-detection or error-correction scheme of some sort). Figure 8.9 shows the constituents of a typical data packet.
The exact constituents of a packet depend on the communication protocol. In general, however, all packets have much the same construction. They begin with a symbol or character string that allows systems listening in to the communication channel to recognize the bit-pattern that follows as a packet.
Each packet bears an address that tells where it is bound. Devices listening in on the communication channel check the address. If it does not match their own or does not indicate that the packet is being broadcast to all devices—in other words, the packet wears an address equivalent to “occupant”—the device ignores the rest of the packet. Communications equipment is courteous enough not to listen in on messages meant for someone else.
Most packets include some kind of identifying information that tells the recipient what to do with the data. For example, a packet may bear a market to distinguish commands from ordinary data.
The bulk of the packet is made from the data being transmitted. Packets vary in size, and hence, the amount of data that they may contain. Although there are no hard-and-fast limits, most packets range from 256 to 2048 bytes.
Error-Handling
Of course, a perfect world would also have fairies and other benevolent spirits to help usher the data along and protect it from all the evil imps and energies lurking about trying to debase and disgrace the singular purity of serial transfer.
The world is, alas, not perfect, and the world of computers is even less so. Many misfortunes can befall the vulnerable serial data bit as it crawls through its connection. One of the bits of a full byte of data may go astray, leaving a piece of data with a smaller value on arrival as it had at departure—a problem akin to shipping alcohol by a courier service operated by dipsomaniacs. With the vacancy in the data stream, all the other bits will slip up a place and assume new values. Or the opposite case—in the spirit of electronic camaraderie, an otherwise well-meaning signal might adopt a stray bit like a child takes on a kitten, only to later discover the miracle of pregnancy and a progeny of errors that ripple through the communications stream, pushing all the bits backward. In either case, the prognosis is not good. With this elementary form of serial communications, one mistaken bit either way, and every byte that follows will be in error.
Establishing reliable serial communications means overcoming these bit-error problems and many others as well. Thanks to some digital ingenuity, however, serial communications work and work well—well enough that you and your computer can depend on them. Because no communication channel is error free, most packets include error-detection or error-correction information. The principle behind error detection is simple: Include duplicate or redundant information that you can compare to the original. Because communication errors are random, they are unlikely to affect both of two copies of the transmitted data. Compare two copies sent along and if they do not match, you can be sure one of them changed during transmission and became corrupted.
Many communications systems don’t rely on complex error-correction algorithms as are used in storage and high-quality memory systems. Communications systems have a luxury storage systems do not: They can get a second chance. If an error occurs in transmission, the system can try again—and again—until an error-free copy gets through.
As a function of communication protocol, packets are part of the software standard used by the communication system. Even so, they are essential to making the hardware—the entire communication system—work properly and reliably.
Control
In a perfect world, a single circuit—nothing more than two wires, a signal line, and a ground—would be all that was necessary to move this serial signal from the one place to another without further ado. But such a serial connection would be like a fire hose squirting out a big, fat stream of bits without rhyme, reason, or nozzle. There’s nothing to control the flow of data. If the receiving end of the serial channel can’t keep up with the sending end, data might flood out every which way and drown the poor recipient.
Laugh if you want, but controlling the flow of data is a major issue of the designers of serial communications systems. Engineers working on the problem have come up with not one but several solutions. Some add an extra connection just for controlling the data flow, a technology called hardware flow control. Some reserve special character values in the data stream to produce software flow control. And some take a further step and redefine the flow of data into digestible chunks and provide a software-based control system built in to these chunks. This system, quickly becoming the most popular, is termed packetized communications.
One difference between these three technologies is range related. Hardware flow control, with its need for extra physical connections, naturally limits its application to short ranges, typically connections between computers and peripherals. Adding the extra wires for control is a small burden when they only need to go a few feet. But the cost and complexity of those wires quickly gets out of hand when distances stretch to miles and signals must go through switching or routing centers. Software flow control works with any range because it requires only a single data pathway. However, because it relies on some of the characters in the data stream and only a few characters can be reserved without compromising the capacity of the channel, it works best only in one-on-one communications. That is, software flow control works best between two devices. Packetized communication, however, has greater versatility. By putting control information into packets, a packet-based system can handle signals meant for a nearly unlimited number of devices. Hence, packetized communications work to link together entire networks.
Hardware and software flow controls are usually reserved for local, direct connections. The most important application for these techniques of flow control is in serial ports, simple links between your computer and its peripherals. single In these applications, flow control is often termed handshaking.
In its most basic form, hardware handshaking adds one signal from the receiving device back to the sending device. This signal has two states: on and off. One state says, “I am ready and willing to accept data from you.” The other state says, “Whoa! I can’t take another byte.” Often these two signals are called ready and busy. The receiving device is in control. When it sends the ready signal, the sending device knows it can send data and does, if it has any ready. When the recipient sends the busy signal back, the sending device stops and waits for the next ready signal.
Software handshaking uses special characters in the data stream to indicate whether they should transfer data. The device receiving data normally sends out one character to indicate it can accept data and a different character to indicate it is busy and cannot accommodate more. In the most common connection system to use software handshaking—the legacy serial port—either of the two characters pairs, XON/XOFF or ETX/ACK, is often used.
In the XON/XOFF scheme, the XOFF character sent from a receiving device to the sending device says to hold off sending data. This character is also sometimes called DC1 and has an ASCII value of 19 or 013(hex). It is sometimes called Control-S. When the receiving device is ready to receive data again, it sends out XON, also known as DC3, to the sender. This character has an ASCII value of 17 or 011(hex). It is sometimes called Control-Q.
ETX/ACK works similarly. ETX, which is an abbreviation for end text, says to hold off on sending more text. This character has an ASCII value of 3 (decimal or hexadecimal) and is sometimes called Control-C. ACK, short for acknowledge, says to resume sending data. It has an ASCII value of 6 (decimal or hexadecimal) and is sometimes called Control-F.
There’s no issue as to whether hardware or software flow control is better. Both work, and that’s all that’s necessary. The important issue is what kind of flow control is used in asingle given system. Both ends must use the same handshaking, even the same characters.