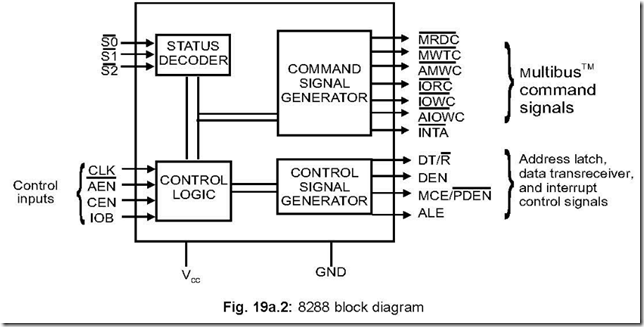
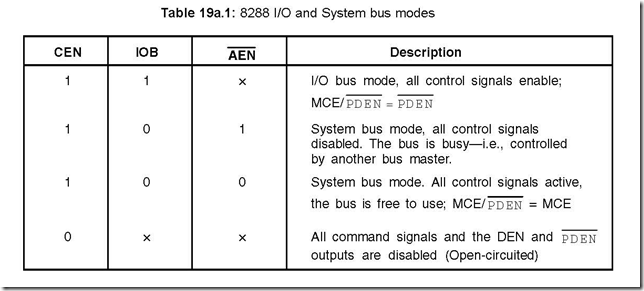
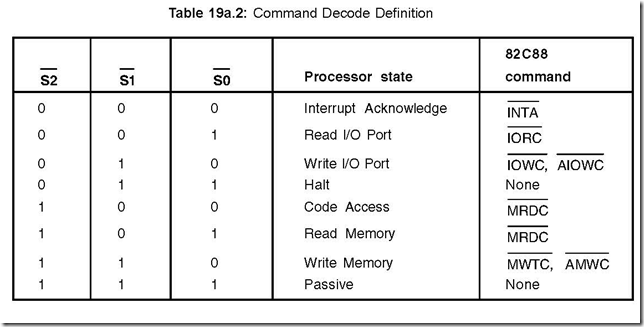
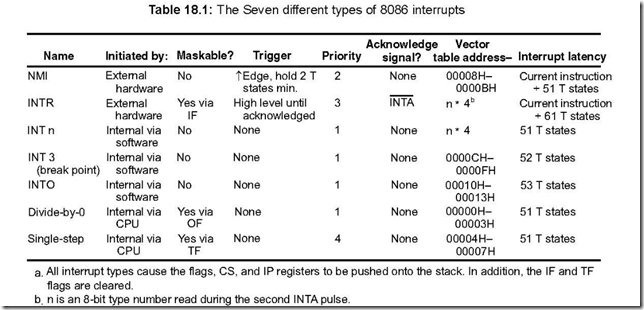
The Underpinnings of Digital Electronics
If you were asked to define what a bit is, chances are you would probably do a pretty good job, saying something like:
A bit is something that can only have two values: on or off.
Instead of ‘‘on or off ’’, you might have used terms for two values like ‘‘one or zero’’, ‘‘high or low voltage’’, ‘‘up or down’’, ‘‘empty or full’’ or (if you fancy yourself as being erudite) ‘‘dominant or recessive’’. All of these terms are correct and imply that the two values are at opposite extremes and are easily differentiated.
When you think of ‘‘bits’’, you are probably thinking of something in a wire or an electronic device contained within a computer, but when the concept of binary (two state) logic was first invented, the values that were
applied were tests to see if a statement was ‘‘true’’ or ‘‘false’’. Examples of true and false statements are:
● The sun always rises in the East. (true)
● Dogs live at the bottom of the ocean like fish. (false)
Looking at these simple statements determining if they are true or false seems to reduce the information within to an extreme degree. The truthfulness of a statement can be combined with another statement to help determine if a more complex postulate is true. If you consider the following ‘‘true’’ statements:
● A dog has fur over its body.
● A dog has four legs.
● Animals have four legs and fur.
● Humans have two legs.
● A snake has scales on its body.
● A reptile’s body has scales or smooth skin.
and combining them together, you can make some surprisingly complex ‘‘assertions’’ from these data using three basic operations. These three basic operations consist of ‘‘AND’’ which is true if all the statements combined together by the AND are true, ‘‘OR’’ which is true if any of the combined statements are true and ‘‘NOT’’ which is true if a single statement is false. To differentiate these three operations from their prose synonyms, I will capitalize them (as well as other basic logic operations) throughout the book. These operations are often called ‘‘logic operations’’ because they were first used to understand the logic of complex philosophical statements.
From the seven statements above and using these three basic operations, you can make the following true assertions:
● Humans are not dogs.
● A dog is an animal.
● A snake is a reptile.
The first statement is true because we know that a human has two legs (violating a condition that is required for the definition of a dog to be true). This is an example of the ‘‘negation’’ or ‘‘NOT’’ operation; the assertion is true if the single input statement is false:
The room is dark because the lights are not on.
The NOT function is often called an ‘‘Inverter’’ because it changes the value of the input from high to low and vice versa.
The second assertion, ‘‘A dog is an animal’’, is true because both of the two statements concerning animals are true when applied to dogs (which have four legs and fur). This is an example of the ‘‘AND’’ operation; the assertion is true if and only if the input statements are true. The AND operation has two or more input statements. In trying to differentiate bicycles and motorcycles from cars, you might make the assertion which uses the AND operation:
A car has four wheels and a motor.
The last assertion, ‘‘A snake is a reptile’’, is true because one of the two statements giving the necessary characteristics for a reptile is true. This is an example of an ‘‘inclusive or’’ (usually referred to as just ‘‘OR’’) operation; the assertion is true if any of the input statements are true. Like the ‘‘and’’ operation, OR can have two or more input statements. If you’re a parent, you will be familiar with the assertion:
During the course of a day, a baby eats, sleeps, cries or poops.
I use this example to illustrate an important point about the ‘‘OR’’ operation that is often lost when it is used in colloquial speech: if more than one input statement is true, the entire assertion is still true. As incredible as it sounds to someone who has not had children yet, a baby is very capable of performing all four actions listed above simultaneously (and seemingly constantly).
I’m making this point because when we speak, we usually use the ‘‘exclusive or’’ instead of ‘‘inclusive or’’ to indicate that only one of two actions can be true. An example statement in which an ‘‘exclusive or’’ is used in everyday speech could be:
Tom is at a restaurant or the movies.
This is an example of ‘‘exclusive OR’’ because Tom can only be at one of the two places at any given time. I will discuss the ‘‘exclusive or’’ operation in more detail later in this chapter, but for now try to remember that an assertion using the ‘‘OR’’ operation will be true if one or more of the input statements are true.
So far I have been working with ‘‘bits’’ of ‘‘binary’’ information contained in ‘‘statements’’ and ‘‘assertions’’. You are probably wondering why a term like ‘‘bit electronics’’ or ‘‘binary electronics’’ is used instead of ‘‘digital electronics’’. ‘‘Digital’’ comes from the Latin word for ‘‘fingers’’ and indicates that there are many discrete signals that are at one of two values. Naming the circuitry ‘‘bit electronics’’ or ‘‘binary electronics’’ would imply that it can only work with one piece of information; digital electronic circuits
can process many bits of information simultaneously, either as separate pieces of information or collections of large amounts of data.
In the first few pages of this book, I have introduced you to the concept of the ‘‘bit’’, the ‘‘digit’’, the ‘‘NOT’’, ‘‘AND’’ and ‘‘OR’’ operations along with the ‘‘exclusive OR’’. Different combinations of these concepts are the basis for the majority of the material presented through the remainder of this book and any course in digital electronics. I suggest that you read over this chapter and make sure you are completely comfortable with the terms and how they work before going on.
Boolean Arithmetic, Truth Tables and Gates
In the introduction to this chapter, I demonstrated the operation of the three operations ‘‘AND’’, ‘‘OR’’ and ‘‘NOT’’, which can be used to test input values (which are in the form of two state ‘‘bits’’) and produce assertions based on the state of the input bits. The verbose method I used could be used with digital electronics, but you will find that it is cumbersome and not intuitively obvious when you are working with electronic circuits. Fortunately, a number of different tools have been developed to simplify working with logic operations.
The first tool that simplifies how logic operations are expressed is known as ‘‘Boolean arithmetic’’ (or sometimes as ‘‘Boolean logic’’), a branch of mathematics where a mathematical expression is used to express how bit inputs can be transformed into an output using the three operations presented in the introduction. Boolean arithmetic was first described by the English mathematician Charles Lutwidge Dodgson, whom you may be familiar with by his nom de plume Lewis Carroll, and expanded upon by George Boole, in the mid 19th century, as a way of understanding, proving or disproving complex philosophical statements. Boole demonstrated that a statement, involving bits of data and the AND, OR or NOT operations could be written in the form:

The braces (‘‘{‘‘ and ’’}’’) are often used to indicate that what’s inside them is optional and the three periods (‘‘.. .’’) indicate that the previous text can be repeated. Using these conventions you can see that a Boolean arithmetic statement is not limited to just one operation with two input bits – they can actually be very lengthy and complex with many bit inputs and multiple operations.
To demonstrate how a Boolean arithmetic statement could be articulated, I can write the proof that a dog is an animal in the form:

If both statements within the parentheses are true, then the ‘‘Result’’ will be true.
This method of writing out assertions and the logic behind them is quite a bit simpler and much easier to understand, but we can do better. Instead of writing out the true or false statement as a condition, it can be expressed in terms of a simple ‘‘variable’’ (like ‘‘X’’). So, if we assign ‘‘A’’ as the result of testing if dogs have four legs and ‘‘B’’ as the result of testing if dogs have fur, we can write out the Boolean arithmetic equation above as:
Result =A AND B
To further simplify how a logic operation is written out, the basic characters ‘‘.’’, ‘‘+’’ and ‘‘!’’ can be used instead of AND, OR and NOT, respectively. AND behaves like a binary multiplication, so along with the ‘‘.’’ character, you may see an ‘‘x’’ or ‘‘*’’. The OR operation may be represented as ‘‘|’’. The ampersand (‘‘&’’) for AND and ‘‘|’’ for OR are often used because they are the same symbols as are used in most computer programming languages. When I write out Boolean arithmetic equations throughout the book, I will be using the ‘‘.’’, ‘‘+’’ and ‘‘!’’ characters for the three basic logic operations instead of the full words.
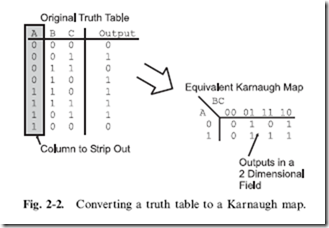
An important advantage of converting a statement into a simple equation is that it more clearly shows how the logic operation works. If the variables ‘‘A’’ and ‘‘B’’ were just given the values of ‘‘true’’ or ‘‘false’’, the ‘‘Result’’ of the equation above could be written out in the form shown in Table 1-1. This is known as a ‘‘truth table’’ and it is a very effective way of expressing how a Boolean operator works. The truth table is not limited to just three inputs,
Table 1-1 ‘‘AND’’ operation truth table using Gray code inputs.
|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘AND’’ Output
|
|
False
|
False
|
False
|
|
False
|
True
|
False
|
|
True
|
True
|
True
|
|
True
|
False
|
False
|
and a function with more than one Boolean operator can be modeled in this way. Functions with more than one output can be expressed using the truth table, but I don’t recommend doing this because relationships between inputs and outputs (which I will discuss in greater detail later in the book) can be obscured.
One other thing to notice about the truth table is that I have expressed the inputs as a ‘‘Gray code’’, rather than incrementing inputs. Gray codes are a technique for sequencing multiple bits in such a way that only one bit changes from one state to the next. Incrementing inputs behave as if the inputs were bits of a larger binary number and the value of this number is increased by one when moving from one state to the next. The truth table above, for the ‘‘AND’’ gate could be written out using incrementing inputs as Table 1-2.
In many cases, truth tables are introduced with incrementing inputs, but I would like to discourage this. Incrementing inputs can obscure relationships between inputs that become obvious when you use Gray codes. This advantage will become more obvious as you work through more complex logic operations and are looking for ways to simplify the expression.
The OR operation’s truth table is given in Table 1-3, while the NOT operation’s truth table is shown in Table 1-4.
The OR operation would be written in Boolean arithmetic, using the ‘‘þ’’ character to represent the OR operation as:
Output = A + B
and the NOT operation (using the ‘‘!’’ character) is written out in Boolean arithmetic as:
Output = !A
Table 1-2 ‘‘AND’’ operation truth table using incrementing inputs.
|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘AND’’ Output
|
|
False
|
False
|
False
|
|
False
|
True
|
False
|
|
True
|
False
|
False
|
|
True
|
True
|
True
|
Table 1-3 ‘‘OR’’ operation truth table using Gray code inputs.
|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘OR’’ Output
|
|
False
|
False
|
False
|
|
False
|
True
|
True
|
|
True
|
True
|
True
|
|
True
|
False
|
True
|
Table 1-4 ‘‘NOT’’ operation truth table using Gray code inputs.
|
Input
|
‘‘NOT’’ Output
|
|
False
|
True
|
|
True
|
False
|
Sometimes, when a signal is NOTted, its symbol is given either a minus sign (‘‘-‘‘) or an underscore (‘‘_’’) as its first character to indicate that it has been inverted by a NOT operation.
The final way of expressing the three basic logic operations is graphically with the inputs flowing through lines into a symbol representing each operation and the output flowing out of the line. Figures 1-1 through 1-3 show the graphical representations of the AND, OR and NOT gates, respectively.
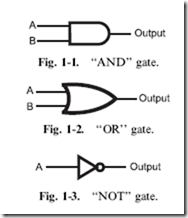
The graphical representation of the logic operations is a very effective way of describing and documenting complex functions and is the most popular way of representing logic operations in digital electronic circuits. When graphics are used to represent the logic operations, they are most often referred to as ‘‘gates’’, because the TRUE is held back until its requirements are met, at which point it is allowed out by opening the gate. ‘‘Gate’’ is the term I will use most often when describing Boolean arithmetic operations in this book.
If you were to replace the lines leading to each gate with a wire and the symbol with an electronic circuit, you can transfer a Boolean arithmetic design to a digital electronic circuit directly.
The Six Elementary Logic Operations
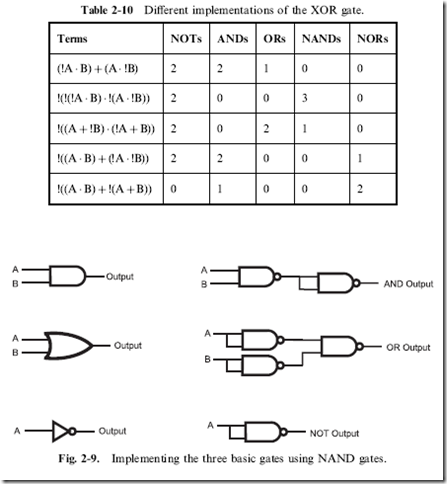
When you look at a catalog of digital electronics chips, you are going to discover that they are built from ANDs, ORs and NOTs as well as three other elementary gates. Two of these gates are critically important to understand because they are actually the basis of digital logic while the third is required for adding numbers together.
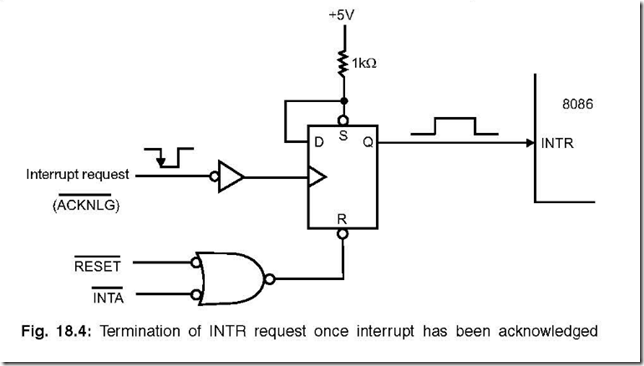
TTL logic is based on the ‘‘NAND’’ gate which can be considered a ‘‘NOTted AND’’ – the output of an AND gate is passed through a NOT gate as shown in Fig. 1-4. Instead of drawing the NAND gate as an AND gate and NOT gate connected together as in Fig. 1-4, they are contracted into the one symbol shown in Fig. 1-5. It’s truth table is in Table 1-5.
When writing out the NAND function in Boolean arithmetic, it is normally in the form:
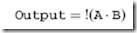
which is a literal translation of the operation – the inputs are ANDed together and the result is NOTted before it is passed to the Output.
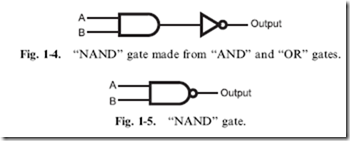
Table 1-5 ‘‘NAND’’ operation truth table.
|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘NAND’’ Output
|
|
False
|
False
|
True
|
|
False
|
True
|
True
|
|
True
|
True
|
False
|
|
True
|
False
|
True
|
 Fig. 1-6 ‘‘NOR’’ gate.
Fig. 1-6 ‘‘NOR’’ gate.
You will see the small circuit on various parts in different electronic devices, both on inputs and outputs. The small circle on the NAND gate is the conventional shorthand symbol to indicate that the input or output of a gate is NOTted.
In case you didn’t note the point above, the NAND gate is the basis for TTL logic, as I will explain later in the book. Being very comfortable with NAND gates is very important to being able to design and use TTL electronics. This is a point that I find is not stressed enough in most electronics courses and by having a strong knowledge of how NAND gates
work as well as how they are implemented you will better understand what is happening within your digital electronics circuits. If you are going to be working with CMOS logic, in the same way you should be comfortable with the NAND gate for TTL, you should be familiar with the ‘‘NOR’’ gate (Fig. 1-6). The NOR gate ca be considered to be a contraction of the OR and NOT gates (as evidenced by the circle on the output of the OR gate) and operates in the opposite manner as the OR gate, as shown in Table 1-6. When using NOR operations in Boolean arithmetic, a similar format to the NAND gate is used:
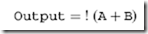
The last elementary logic gate that you will have to work with is the ‘‘Exclusive OR’’ (Fig. 1-7) with Table 1-7 being its truth table. The
Table 1-6 ‘‘NOR’’ operation truth table.
|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘NAND’’ Output
|
|
False
|
False
|
True
|
|
False
|
True
|
False
|
|
True
|
True
|
False
|
|
True
|
False
|
False
|
 Fig. 1-7. ‘‘XOR’’ gate.
Fig. 1-7. ‘‘XOR’’ gate.
Table 1-7 ‘‘Exclusive OR’’ operation truth table.
|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘Exclusive OR’’ Output
|
|
False
|
False
|
False
|
|
False
|
True
|
True
|
|
True
|
True
|
False
|
|
True
|
False
|
True
|
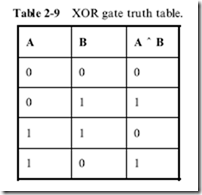
Exclusive OR (also referred to as ‘‘Ex-OR’’ or ‘‘XOR’’) only returns a True output if only one of its inputs is true. If both inputs are the same, then the Exclusive OR outputs False. The Boolean arithmetic symbol for Exclusive OR is often a caret (‘‘^’’) as is used in computer programming languages or a circle with an ‘‘x’’ character in it ®. Writing a Boolean statement with the Exclusive OR would be in the format:
Output = A ^ B
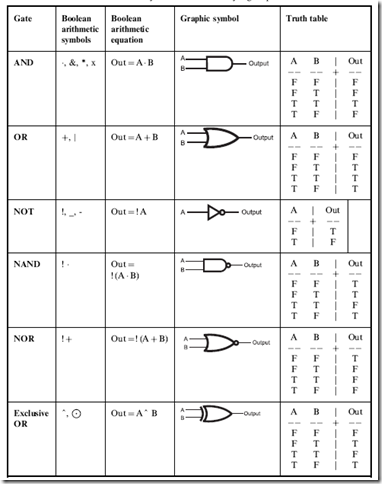
Table 1-8 summarizes the six elementary gates along with their Boolean arithmetic symbols and formats, graphical symbols and truth tables.
Table 1-8 Summary of the six elementary logic operations.
Combinatorial Logic Circuits: Combining Logic Gates
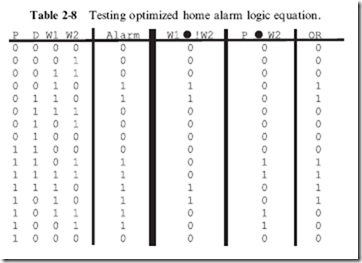
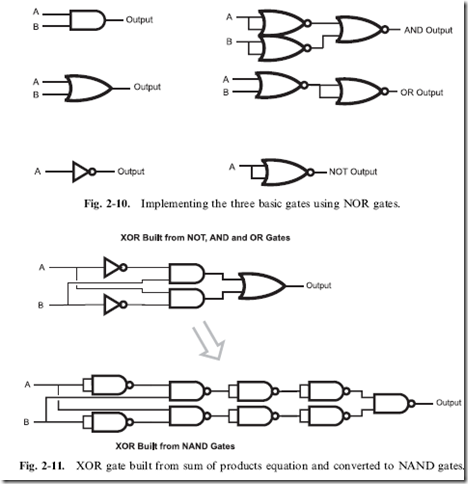
As I hinted at in the previous section, multiple gate functions can be combined to form more complex or different Boolean logic functions. Wiring together multiple gates are used to build a complex logic function that only outputs a specific value when a specific combination of True and False inputs are passed to it is known as ‘‘combinatorial logic’’. The output of a combinatorial logic circuit is dependent on its input; if the input changes then the output will change as well.
When I wrote the preceding paragraph, I originally noted that combinatorial logic circuits produce a ‘‘True’’ output for a given set of inputs. This is incorrect, as there will be some cases where you will require a False output in your application. I made the definition a bit more ambiguous so that you do not feel like the output has to be a single, specific value when the input consists of the required inputs. It is also important to note that in a combinatorial logic circuit, data flows in one direction and outputs in logic gates cannot be used as inputs to gates which output back to themselves. These two points may seem subtle now, but they are actually critically important to the definition of combinatorial logic circuits and using them in applications. An example of a combinatorial circuit is shown in Fig. 1-8. In this circuit, I have combined three AND gates, a NOR gate, a NOT gate and an XOR gate to produce the following logic function:
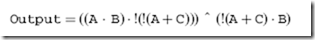
This combinatorial circuit follows the convention that inputs to a gate (or a chip or other electronic component) are passed into the left and outputs
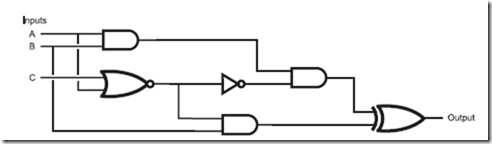
Fig. 1-8 Combinatorial circuit built from multiple logic gates.
exit from the right. This will help you ‘‘read’’ the circuit from left to right, something that should be familiar to you.
While seeing a series of logic gates, like the one in Fig. 1-8, seems to be overwhelming, you already have the tools to be able to work through it and understand how it works. In the previous section, I noted that gates could be connected by passing the output of one into an input of another; a combinatorial circuit (like Fig. 1-8) is simply an extension of this concept and, being an extension, you can use the same tools you used to understand single gates to understand the multiple gate operation.
should point out that the two broken lines on the left side of Fig. 1-8 (leading down from ‘‘A’’ and ‘‘B’’) indicate that these lines are not connected to the lines that they intersect with. You will find that it can be very difficult to design logic circuits without connected and separate lines from becoming confused. In Fig. 1-9, I have shown a couple of the conventional ways of drawing intersecting lines, depending on whether or not they connect or bypass each other. Probably the most intuitively obvious way of drawing connecting and bypassing lines is to use the dot and arc, respectively. I tend not to because they add extra time to the logic (and circuit) diagram drawing process. As you see more circuit diagrams, you will see the different conventions used and you should be comfortable with recognizing what each means.
![image_thumb[1] image_thumb[1]](http://lh5.ggpht.com/-hnn51kQAjto/VGdrfLSJR7I/AAAAAAAA0XA/d8pRjL4PoSQ/image_thumb%25255B1%25255D_thumb.png?imgmax=800)
Fig. 1-9. Different representations for wires that connect or bypass.
![image_thumb[2] image_thumb[2]](http://lh3.ggpht.com/-oekEJ-HUggM/VGdriFzfyUI/AAAAAAAA0XQ/KXSx9im9s48/image_thumb%25255B2%25255D_thumb.png?imgmax=800)
Fig. 1-10. Combinatorial circuit with logic gate outputs marked.
When I am faced with a complex combinatorial circuit, the first thing I do is to mark the outputs of each of the gates (Fig. 1-10) and then list them according to their immediate inputs:
![image_thumb[3] image_thumb[3]](http://lh5.ggpht.com/-1YnPRwPBEPs/VGdrkte7hzI/AAAAAAAA0Xg/B7o5WecY86E/image_thumb%25255B3%25255D_thumb.png?imgmax=800)
After listing them, I then work through a truth table, passing the outputs of each gate along until I have the final outputs of the complete function (Table 1-9). In keeping with my comments of the previous section, I have used a three bit Gray code for the inputs to this circuit.
Before going on, there are two points that I would like you to keep in the back of your mind. First, this is actually quite an efficient methodology for decoding combinatorial circuits that you are given the design for. Designing a logic gate circuit that responds in a specific manner is actually quite a different process and I will be devoting the rest of this chapter as well as the next to explaining the design and optimization of combinatorial circuits. Once you have finished with Chapter 2, you might want to revisit the example circuit in Fig. 1-8 and see how effectively you can reduce its complexity and the number of logic gates needed to implement it. The second point that you should be aware of is the example circuit that I used in this section is actually quite unwieldy and does not conform to the typical methods used to design most practical combinatorial digital electronic circuits. In the next section, I will present you with the conventional methods for specifying and documenting combinatorial circuits.
Table 1-9 Decoding the response of the combinatorial circuit in Fig. 1-8.
![image_thumb[4] image_thumb[4]](http://lh5.ggpht.com/-fdFS7K0QKtI/VGdroOzVzSI/AAAAAAAA0Xw/zyxWdPEKkIc/image_thumb%25255B4%25255D_thumb.png?imgmax=800)
Sum of Products and Product of Sums
Presenting combinatorial circuits as a collection of gates wired together almost randomly, like the circuit shown in Fig. 1-8, is sub-optimal from a variety of perspectives. The first is, the function provided by the combinatorial circuit is not obvious. Secondly, using a variety of different gates can make your parts planning process difficult, with only one gate out of many available in a chip being used. Lastly, the arrangement of gates will be difficult for automated tools to combine on a printed circuit board (‘‘PCB’’) or within a logic chip. What is needed is a conventional way of drawing combinatorial logic circuits.
The most widely used format is known as ‘‘sum of products’’. Earlier in the chapter, I presented the concept that the AND operation was analogous to multiplication just as the OR operation is to addition. Using this background, you can assume that a ‘‘sum of products’’ circuit is built from AND and OR gates. Going further, you might also guess that the final output is the ‘‘OR’’ (because addition produces a ‘‘sum’’) with the gates that
![image_thumb[5] image_thumb[5]](http://lh6.ggpht.com/-S28DzIQ1CG0/VGdrrVtJHwI/AAAAAAAA0YA/uMmsdwPFPxg/image_thumb%25255B5%25255D_thumb.png?imgmax=800)
Fig. 1-11. Example ‘‘sum of products’’ combinatorial logic circuit.
convert the inputs being ‘‘AND’’ gates (a ‘‘product’’ is the result of a multiplication operation). An example ‘‘sum of products’’ combinatorial logic circuit is shown in Fig. 1-11.
In this circuit, the inputs are ANDed together and the result is passed to an OR gate. In this circuit, the output will be ‘‘True’’ if any of the inputs to the OR gate (which are the outputs from the AND gates) are true. In some cases, to make sure that the inputs and outputs of the AND gates are in the correct state, they will be inverted using NOT gates, as I have shown in Fig. 1-11.
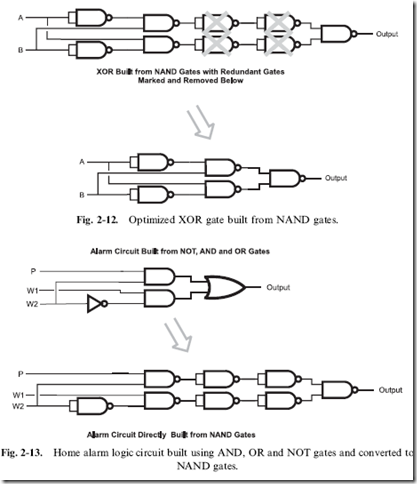
Figure 1-11 has one feature that I have not introduced to you yet and that is the three input OR gate on the right side of the diagram. So far, I have only discussed two input gates, but I should point out that three input gates can be built from multiple two input gates, as I show in Fig. 1-12, in which two, two input AND gates are combined to form a single three input AND gate. A three input OR gate could be built exactly the same way.
A three input NAND or NOR gate is a bit trickier, as Fig. 1-13 shows. For this case, the output of the NAND gate processing ‘‘A’’ and ‘‘B’’ must be inverted (which can be accomplished with a NAND gate and both inputs tied together as I show in Fig. 1-13) to make its output the same as an ‘‘AND’’. The NAND gate’s function is to first AND its inputs together and then invert them before driving out the output signal. As I will explain in greater detail in the next chapter, an inverted output, when it is inverted, becomes a ‘‘positive’’ output and I use this rule to produce the three input NAND gate. A three input NOR gate would be built in exactly the same way as a three input NAND gate.
![image_thumb[6] image_thumb[6]](http://lh3.ggpht.com/-YBexnUgPTzI/VGdruW_Ob7I/AAAAAAAA0YQ/ijiehzYDrz8/image_thumb%25255B6%25255D_thumb.png?imgmax=800)
Along with having a ‘‘sum of products’’ combinatorial logic circuit that outputs a True when one of the intermediate AND gates outputs True, there is the complementary ‘‘product of sums’’ (Fig. 1-14), which outputs False when one of its intermediate OR gates outputs False.
While product of sums combinatorial circuits can produce the same functions as sum of product combinatorial circuits, you will not see as many product of sum combinatorial circuits in various designs because they rely on what I call ‘‘negative logic’’. Most people cannot easily visualize something happening because the inputs do not meet an expected case, which is exactly what happens in a product of sums combinatorial logic circuit.
To demonstrate how a sum of product combinatorial logic circuit is designed, consider the messy combinatorial logic circuit I presented
![image_thumb[7] image_thumb[7]](http://lh5.ggpht.com/-EtC6BTpDv_4/VGdryGwtOxI/AAAAAAAA0Yg/zGGlj9BcT_c/image_thumb%25255B7%25255D_thumb.png?imgmax=800)
Fig. 1-14. Example ‘‘product of sums’’ combinatorial logic circuit.
in the previous section (see Fig. 1-8). To understand the operation of this circuit, I created a large truth table (Table 1-9) and listed the outputs of each of the intermediate gates and finally discovered that the function output True in three cases that can be directly translated into AND operations by assuming that in each case the output was true and the input conditions were all true. To make all three inputs True to the AND gates when the input is False, I invert them and came up with the three statements below:
A : B · !C
A · B · C
!A · B · !C
These three AND statements can be placed directly into a sum of products combinatorial circuit, as shown in Fig. 1-15.
Looking at Fig. 1-15, you’ll probably notice that this circuit has the same total number of gates as the original circuit – and, assuming that each three input gate is made up of two, two input AND gates, it probably requires four more gates than the original circuit shown in Fig. 1-8. The only apparent advantage to the sum of product format for combinatorial logic circuit is that it is easier to follow through and see that the output is True for the three input conditions I listed above.
In the following chapters, I will introduce you to combinatorial logic circuit optimization as well as explain in more detail how digital electronic gates are actually built. It will probably be surprising to discover that the sum
![image_thumb[8] image_thumb[8]](http://lh5.ggpht.com/-UqUYnW0MS18/VGdr1ON9GGI/AAAAAAAA0Yw/poroMRr2-T4/image_thumb%25255B8%25255D_thumb.png?imgmax=800)
of product combinatorial logic circuit format leads to applications that are more efficient (in terms of total gate or transistor count along with speed and heat dissipation) than ones using less conventional design methodologies.
Waveform Diagrams
So far in this chapter, I have shown how logic functions can be presented as English text, mathematical equations (Boolean arithmetic), truth tables and graphical circuit diagrams. There are actually two more ways in which the logic data can be presented that you should be familiar with. The first method is not one that you will see a lot of except when debugging microprocessor instructions from a very low level, while the second is one that you will have to become very familiar with, especially when the digital electronic signals pass from the combinatorial logic shown here to more complex circuits that have the ability to ‘‘store’’ information.
The first method, the ‘‘state list’’ consists of a list of text columns for each state of the circuit. The state list is really a compressed form of the truth table and is best suited for displaying a fairly large amount of numerical data. Going back to the example circuit of Fig. 1-8, and Table 1-9, I could express the truth table as the series of columns below. Note that I have used the numeric values ‘‘1’’ for True and ‘‘0’’ for False because they are easier to
differentiate than ‘‘T’’ and ‘‘F’’ over a number of rows.
![image_thumb[9] image_thumb[9]](http://lh6.ggpht.com/-8040xzQwgTA/VGdr3yMHYNI/AAAAAAAA0ZA/dpeSgiS4dIY/image_thumb%25255B9%25255D_thumb.png?imgmax=800)
As I said, not a lot of information is obvious from the state list. Some format- ting could be done to make the inputs and outputs better differentiated, but for the most part, I don’t recommend using state lists for most digital electronics applications. Where the state list is useful is in debugging state machine or microcontroller applications in which you have added hardware to the data, address and control busses to record how the device responds to specific inputs.
The state list is not ideal for this type of application, but it’s better than nothing. The other method, which is not only recommended as a circuit analysis and design tool but is also one you should be intimately familiar with is the ‘‘waveform diagram’’. Waveforms are electrical signals that have been plotted over time. The original waveform display tool was the oscilloscope; a drawing of a typical oscilloscope’s display is shown in Fig. 1-16.
![image_thumb[10] image_thumb[10]](http://lh6.ggpht.com/-4t96gBJCaEU/VGdr6rP012I/AAAAAAAA0ZQ/OrKfhWiBFDM/image_thumb%25255B10%25255D_thumb.png?imgmax=800)
The features of the two ‘‘waveforms’’ displayed on the oscilloscope screen can be measured by placing them against the ‘‘graticule markings’’ on the display. These markings (usually just referred to as ‘‘graticules’’ and etched onto the glass screen of the oscilloscope) are indicators of a specific passage of time or change in voltage. Along with the ‘‘gross’’ graticules, most oscilloscopes have finer markings, to allow more accurate measurements by moving the waveforms over them.
Oscilloscopes are very useful tools for a variety of different applications, which contain varying voltage levels (which are known as ‘‘analog’’ voltage levels). They can be (and often are) used for digital logic applications but they are often not the best tool because digital waveforms only have two levels, when applied to electronics: digital signals are either a high voltage or a low voltage. The timing of the changes of these two voltage levels is more interesting to the designer.
So instead of thinking of digital waveforms in terms of voltage over time, in digital electronics, we prefer to think of them as states (High/Low, True/ False, 1/0) over time and display them using a waveform diagram like the one shown in Fig. 1-17. When designing your digital electronics circuit, you will create a waveform diagram to help you understand how the logic states will be passed through the circuit; later, when you are debugging the circuit, you will be comparing what you actually see with this diagram to see if your assumptions about how the circuit would operate are correct. The different signals shown in Fig. 1-17 are samples of what you will see when you are designing your own application circuit.
![image_thumb[11] image_thumb[11]](http://lh5.ggpht.com/-6yWOC_ncUso/VGdr9tVzN6I/AAAAAAAA0Zg/WlmiW1zyzmI/image_thumb%25255B11%25255D_thumb.png?imgmax=800)
![image_thumb[12] image_thumb[12]](http://lh4.ggpht.com/-YcDDkcXFbzU/VGdsBdcPXeI/AAAAAAAA0Zw/wYHdR0V1xlM/image_thumb%25255B12%25255D_thumb.png?imgmax=800)
The waveform diagram is the first tool that will help you optimize your circuit. Before writing up this section, I was planning on the diagrams I wanted to include with it and one was a waveform representation of the first example combinatorial logic circuit’s operation from Table 1-9. The thin vertical lines indicate the edges of each state.
After drawing out Fig. 1-18, it was obvious that signals ‘‘1’’ and ‘‘4’’ (from the marked circuit diagram Fig. 1-8) were redundant. Looking back at the diagram for the circuit, I realized that the AND gate with output 4 and inverter with output 3 could be completely eliminated from the circuit – the output of AND gate 1 could be passed directly to the XOR gate (with output 6).
The waveform diagram shown in Fig. 1-18 is what I call an ‘‘idealized waveform diagram’’ and does not encompass what is actually happening in a physical circuit. Looking at Fig. 1-18, you will see that I have assumed that the switching time for the gates is instantaneous. In real components, switching time is finite, measurable and can have a significant impact to your application’s ability to work. This is discussed in more detail in later chapters. Finally, this circuit does not allow for basic errors in understanding, such as
what happens when multiple gate outputs are passed to a single gate input – your assumption of this type of case may not match what really happens in an actual circuit.
In this chapter, I have introduced you to the basic concepts of combinatorial logic circuits and the parts that make them up. In the next chapter, I will start working through some of the practical aspects of designing efficient digital electronic circuits.
Quiz
1. Which of the following statements is true?
(a) Negative logic is the same as reverse psychology. You get some body to do something by telling them to do what you don’t want them to do
(b) Using the logic definition, ‘‘A dog has four legs and fur’’, a cat could be accurately described as a dog
(c) ‘‘High’’ and ‘‘Higher’’ are valid logic states
(d) Assertions are the same as logic operations
2. Boolean arithmetic is a:
(a) way to express logic statements in a traditional mathematical equation format
(b) terrible fraud perpetrated by philosophers to disprove things they don’t agree with
(c) very difficult calculation used in astronomy
(d) fast way to solve problems around the house
3. The truth table using ‘‘incrementing input’’ for the OR gate is correctly represented as:
(a) ![image_thumb[14] image_thumb[14]](http://lh4.ggpht.com/-hGzvMxoskuM/VGdsD3a9UUI/AAAAAAAA0aA/VPTPAF6UvLw/image_thumb%25255B14%25255D_thumb.png?imgmax=800)

|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘OR’’ Output
|
|
False
|
False
|
False
|
|
False
|
True
|
True
|
|
True
|
False
|
True
|
|
True
|
True
|
False
|
|
|
(c)
|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘OR’’ Output
|
|
False
|
False
|
False
|
|
False
|
True
|
True
|
|
True
|
False
|
True
|
|
True
|
True
|
True
|
|
|
(d)
|
Input ‘‘A’’
|
Input ‘‘B’’
|
‘‘OR’’ Output
|
|
False
|
False
|
False
|
|
False
|
True
|
False
|
|
True
|
False
|
False
|
|
True
|
True
|
True
|
|
|
4. When writing a logic equation, which symbols are typically used to represent optional operations?
(a) {and}
(b) <and>
(c) (and)
(d) [and]
5. If the output of an Exclusive OR gate was passed to a NOT gate’s input, the NOT gate output would be ‘‘True’’ if:
(a) Input ‘‘A’’ was True and input ‘‘B’’ is False
(b) There is only one input and the output would be True if the input was False
(c) A dot was placed on the output of the Exclusive OR symbol
(d) Both inputs were at the same state (either True or False)
6. Boolean arithmetic statements are similar to:
(a) Verbal descriptions of what the logic is to do
(b) HTML, the language used to program an internet web page
(c) Simple mathematical equations
(d) The holes punched into computer cards
7. When decoding a combinatorial logic circuit diagram, you
(a) Write out the Boolean arithmetic equation for the function and list the output for each possible input
(b) Start slamming your forehead on your desk
(c) Give each gate’s output a unique label and list their outputs for each changing circuit input as well as outputs for other gates in the circuit
(d) Rearrange the gates in the diagram to help you understand what the function is doing
8. ‘‘Sum of product’’ combinatorial logic circuits are popular because:
(a) They are the most efficient way of designing circuitry
(b) Their operation can be quickly seen by looking at the circuit diagram
(c) They dissipate less heat than other design methodologies
(d) They are more robust and allow for more reliable product designs
9. When trying to debug a digital clock circuit, what tool is not recommended?
(a) Truth tables
(b) Boolean arithmetic
(c) State lists
(d) Graphical circuit diagrams
10. Waveform diagrams display:
(a) Logic state changes over time
(b) Switching times of digital electronic gates
(c) Problems with line impedance
(d) Voltage variances in a logic signal over time
 By doing this, I can see that the inside terms of the first and third products are identical. Along with this, I can see that the second and fifth products
By doing this, I can see that the inside terms of the first and third products are identical. Along with this, I can see that the second and fifth products 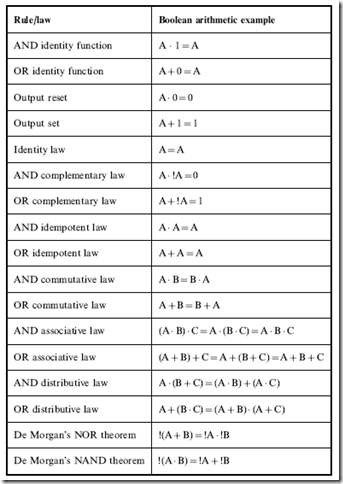

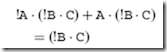
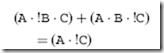












![image_thumb[1] image_thumb[1]](http://lh5.ggpht.com/-hnn51kQAjto/VGdrfLSJR7I/AAAAAAAA0XA/d8pRjL4PoSQ/image_thumb%25255B1%25255D_thumb.png?imgmax=800)
![image_thumb[2] image_thumb[2]](http://lh3.ggpht.com/-oekEJ-HUggM/VGdriFzfyUI/AAAAAAAA0XQ/KXSx9im9s48/image_thumb%25255B2%25255D_thumb.png?imgmax=800)
![image_thumb[3] image_thumb[3]](http://lh5.ggpht.com/-1YnPRwPBEPs/VGdrkte7hzI/AAAAAAAA0Xg/B7o5WecY86E/image_thumb%25255B3%25255D_thumb.png?imgmax=800)
![image_thumb[4] image_thumb[4]](http://lh5.ggpht.com/-fdFS7K0QKtI/VGdroOzVzSI/AAAAAAAA0Xw/zyxWdPEKkIc/image_thumb%25255B4%25255D_thumb.png?imgmax=800)
![image_thumb[5] image_thumb[5]](http://lh6.ggpht.com/-S28DzIQ1CG0/VGdrrVtJHwI/AAAAAAAA0YA/uMmsdwPFPxg/image_thumb%25255B5%25255D_thumb.png?imgmax=800)
![image_thumb[6] image_thumb[6]](http://lh3.ggpht.com/-YBexnUgPTzI/VGdruW_Ob7I/AAAAAAAA0YQ/ijiehzYDrz8/image_thumb%25255B6%25255D_thumb.png?imgmax=800)
![image_thumb[7] image_thumb[7]](http://lh5.ggpht.com/-EtC6BTpDv_4/VGdryGwtOxI/AAAAAAAA0Yg/zGGlj9BcT_c/image_thumb%25255B7%25255D_thumb.png?imgmax=800)
![image_thumb[8] image_thumb[8]](http://lh5.ggpht.com/-UqUYnW0MS18/VGdr1ON9GGI/AAAAAAAA0Yw/poroMRr2-T4/image_thumb%25255B8%25255D_thumb.png?imgmax=800)
![image_thumb[9] image_thumb[9]](http://lh6.ggpht.com/-8040xzQwgTA/VGdr3yMHYNI/AAAAAAAA0ZA/dpeSgiS4dIY/image_thumb%25255B9%25255D_thumb.png?imgmax=800)
![image_thumb[10] image_thumb[10]](http://lh6.ggpht.com/-4t96gBJCaEU/VGdr6rP012I/AAAAAAAA0ZQ/OrKfhWiBFDM/image_thumb%25255B10%25255D_thumb.png?imgmax=800)
![image_thumb[11] image_thumb[11]](http://lh5.ggpht.com/-6yWOC_ncUso/VGdr9tVzN6I/AAAAAAAA0Zg/WlmiW1zyzmI/image_thumb%25255B11%25255D_thumb.png?imgmax=800)
![image_thumb[12] image_thumb[12]](http://lh4.ggpht.com/-YcDDkcXFbzU/VGdsBdcPXeI/AAAAAAAA0Zw/wYHdR0V1xlM/image_thumb%25255B12%25255D_thumb.png?imgmax=800)
![image_thumb[14] image_thumb[14]](http://lh4.ggpht.com/-hGzvMxoskuM/VGdsD3a9UUI/AAAAAAAA0aA/VPTPAF6UvLw/image_thumb%25255B14%25255D_thumb.png?imgmax=800)