Addition, Subtraction, Multiplication and Division of unsigned and signed numbers

7.3.3 Addition, Subtraction, Multiplication and Division of unsigned and signed numbers

The procedure for addition and subtraction of two’s complement signed binary numbers

is straightforward. The procedure for adding unsigned numbers is discussed in Chapter

2. Also, addition of two 2’s complement signed numbers was included in Chapter 2. Note that binary numbers represented in two’s complement form contain both unsigned numbers (Most Significant Bit= 0) and signed numbers (Most Significant Bit= 1). The procedure for adding two 2’s complement signed numbers using pencil and paper is provided below:

Add the two numbers along with the sign bits. Check the overflow bit (V) using V = Cr 81 Cp where Cr is the final carry and CP is the previous carry. If V = 0, then the result of addition is correct. On the other hand, if V = 1, then the result is incorrect; one needs to increase the number of bits for each number, and repeat the addition operation until V = 0 to obtain the correct result.

Subtraction of two 2’s complement signed binary numbers using pencil and paper can be performed as follows:

Take the 2’s complement of subtrahend along with the sign bit and add it to the minuend . The result is correct if there is no overflow. The result is wrong if there is an overflow. In case of overflow, increase the number of bits for each number, repeat the subtraction operation until the overflow is zero to obtain the correct result. Note that if there is a final carry after performing the 2’s complement subtraction, the result is positive. On the other hand, if there is no final carry after 2’s complement subtraction, the result is negative.

Computers utilize common hardware to perform addition and subtraction operations for both unsigned and signed numbers. The instruction set of computers typically include the same ADD and SUBTRACT instructions for both unsigned and signed numbers. The interpretations of unsigned and signed ADD and SUBTRACT operations are performed by the programmer. For example, consider adding two 8-bit numbers, A and B (A= FF 16 and B= FF 16 ) using the ADD instruction by a computer as follows:

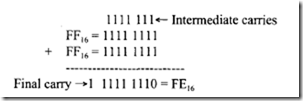When the above addition is interpreted as an unsigned operation by the programmer, the result will be

A+ B =FF 16 + FF₁₆ = 255₁₀+ 255 ₁₀= 510₁₀ which is FE16 with a carry as shown above. However, if the addition is interpreted as a signed operation, then, A+ B =FF 16 + FF16 = (-1₁₀) + (-1₁₀) = -2₁₀ which is FE16 as shown above, and the final carry must be discarded by the programmer. Similarly, the unsigned and signed subtraction can be interpreted by the programmer.

Typical 8-bit microprocessors, such as the Intel 8085 and Motorola 6809, do not include multiplication and division instructions due to limitations in the circuit densities that can be placed on the chip. Due to advances in semiconductor technology, 16-, 32-, and 64-bit microprocessors usually include multiplication and division algorithms in a ROM inside the chip. These algorithms typically utilize an ALU to carry out the operations. one can write a program that multiplies two numbers. Although this solution seems viable, the operational speed is unsatisfactory.

For application environments such as real-time digital filtering, in which the processor is expected to perform 32 to 64 eight-bit multiplication operations within 100

!!Sec (sampling frequency= 10kHz), speed is an important factor. New device technologies such as BICMOS and HCMOS, allow manufacturers to pack millions of transistors in a chip. Consequently, state-of-the-art 32-bit microprocessors such as the Motorola 68060 (HCMOS) and Intel Pentium (BICMOS) designed using these technologies, have a larger instruction set than their predecessors, which includes multiplication and division instructions. In this section, multiplier design principles are discussed. Two unsigned integers can be multiplied using repeated addition as mentioned in Chapter 2. Also, they can be multiplied in the same way as two decimal numbers are multiplied by paper and pencil method. Consider the multiplication of two unsigned integers, where the multiplier Q = 15 and the multiplicand is M = 14, as illustrated:

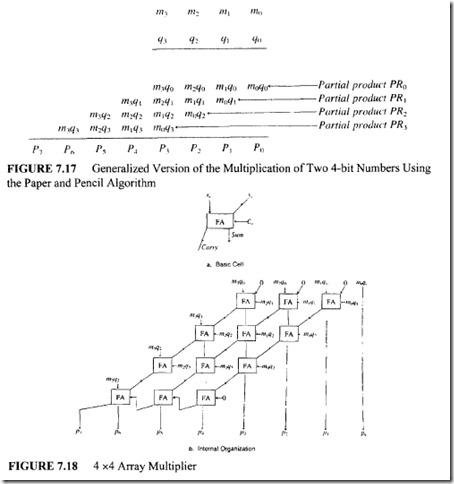
This procedure can be implemented by using combinational circuit elements such as AND gates and FULL adders. Generally, a 4-bit unsigned multiplier Q and a 4-bit unsigned multiplicand M can be written as M: m3 m2 m 1 m0 and Q: q3 q2 q1 q0.The process of generating the partial products and the final product can also be generalized as shown in

Figure 7.17. Each cross-product term (mi q) in this figure can be generated using an AND gate. This requires 16 AND gates to generate all cross-product terms that are summed by full adder arrays, as shown in Figure 7.18.

Consider the generation of p ₂ in Figure 7.18(b). From Figure 7.17, p ₂ is the sum of m₂q_0, m1 q1 and m0q_{2 •} The sum of these three elements is obtained by using two full adders. (See column for p ₂ in Figure 7.18). The top full-adder in this column generates the sum m₂q₀ + m₁q _1• This sum is then added to m₀q₂ by the bottom full-adder along with any carry from the previous full-adder for p _{1 •}

The time required to complete the multiplication can be estimated by considering the longest carry propagation path comprising of the rightmost diagonal (which includes the full-adder for p ₁ and the bottom full-adders for p₂ and p₃ ), and the last row (which includes the full-adder for p₆ and the bottom full-adders for p₄ and p₅). The time taken to multiply  two n-bit numbers can be expressed as follows:

In this equation, all cross-product terms m_iq_i can be generated simultaneously by an array of AND gates. Therefore, only one AND gate delay is included in the equation. Also, the rightmost diagonal and the bottom row contain (n – 1) full-adders each for the n x n multiplier.

Assuming that    be simplified as shown:

T(n) = 2 Δ+ (2n- 2)2Δ = (4n- 2)Δ .

The array multiplier that has been considered so far is known as Braun’s multiplier. The hardware is often called a nonadditive multiplier (NM), since it does not include any additive inputs. An additive multiplier (AM) includes an extra input R; it computes products of the form

P=M*Q+R

This type of multiplier is useful in computing the sum of products of the form };XiYi. Both an NM and an AM are available as standard 1C blocks. Since these systems require more components, they are available only to handle 4- or 8-bit operands.

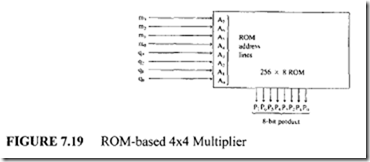
Alternatively, the same 4×4 NM discussed earlier can be obtained using a 256 x 8 ROM as shown in Figure 7.19.

It can be seen that a given MQ pair defines a ROM address, where the corresponding 8-bit product is held. The ROM approach can be used for small-scale multipliers because:

• The technological advancements allow the manufacturers to produce low-cost ROMs.
•  The design effort is minimum.

In case of large multipliers, ROM implementation is unfeasible, since large-size ROMs are required. For example, in order to implement an 8 x 8 multiplier, a 216 x 16 ROM is required. If the required 8 x 8 product is decomposed into a linear combination offour 4×4 products, an 8 x 8 multiplier can be implemented using four 256 x 8 ROMs and a few 4-bit parallel adders. However, PLDs can be used to accomplish this.Signed multiplication can be performed using various algorithms. A simple algorithm follows.

• In the case of signed numbers, there are three possibilities:

I. M and Q are in sign-magnitude form.

2. M and Q are in ones complement form.

3. M and Q are in twos complement form.

For the first case, perform unsigned multiplication of the magnitudes without the sign