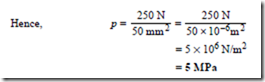This chapter describes fluid pressure, together with buoyancy and hydrostatic stability. The chapter also defines Archimedes’ principle, which is used to determine the buoyancy of boats, yachts, ships, etc. The chapter also describes metacentric height, which is used to determine the hydrostatic stability of the aforementioned vessels, and the explanation of this topic is aided with a number of simple worked examples. The chapters also describe gauges used in fluid mechanics, such as barometers, manometers, and the Bourdon pressure and vacuum gauges. These gauges are used to determine the properties and behaviour of fluids when they are met in practice. Calculations are given of simple floating structures and reference is made to the mid-ordinate rule, described earlier in Chapter 15, which can be used for determining the areas and volumes of complex shapes, such as those often met in naval architecture and civil engineering and many other branches of engineering.
At the end of this chapter you should be able to:
• define pressure and state its unit
• understand pressure in fluids
• distinguish between atmospheric, absolute and gauge pressures
• state and apply Archimedes’ principle
• describe the construction and principle of operation of different types of barometer
• describe the construction and principle of operation of different types of manometer
• describe the construction and principle of operation of the Bourdon pressure gauge
• describe the construction and principle of operation of different types of vacuum gauge
• calculate hydrostatic pressure on submerged surfaces
• understand hydrostatic thrust on curved surfaces
• define buoyancy
• appreciate and perform calculations on the stability of floating bodies
Pressure
The pressure acting on a surface is defined as the perpendicular force per unit area of surface. The unit of pressure is the pascal, Pa, where 1 pascal is equal to 1 newton per square metre. Thus pressure,
where F is the force in newtons acting at right angles to a surface of area A square metres.
When a force of 20 N acts uniformly over, and perpendicular to, an area of 4 m2, then the pressure on the area, p, is given by:
It should be noted that for irregular shaped flat surfaces, such as the water planes of ships, their areas can be calculated using the mid-ordinate rule, described in Chapter 15.
Problem 1. A table loaded with books has a force of 250 N acting in each of its legs. If the contact area between each leg and the floor is 50 mm2, find the pressure each leg exerts on the floor.
That is, the pressure exerted by each leg on the floor is 5 MPa
Problem 2. Calculate the force exerted by the atmosphere on a pool of water that is 30 m long by 10 m wide, when the atmospheric pressure is 100 kPa.
Problem 3. A circular piston exerts a pressure of 80 kPa on a fluid, when the force applied to the piston is 0.2 kN. Find the diameter of the piston.
Now try the following Practise Exercise
Practise Exercise 116 Further problems on pressure
1. A force of 280 N is applied to a piston of a hydraulic system of cross-sectional area 0.010 m2. Determine the pressure produced
by the piston in the hydraulic fluid.
[28 kPa]
2. Find the force on the piston of Question 1 to produce a pressure of 450 kPa. [4.5 kN]
3. If the area of the piston in Question 1 is halved and the force applied is 280 N, determine the new pressure in the hydraulic fluid.
[56 kPa]
Fluid pressure
A fluid is either a liquid or a gas and there are four basic factors governing the pressure within fluids.
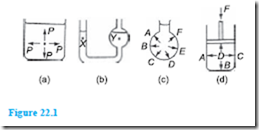
(a) The pressure at a given depth in a fluid is equal in all directions; see Figure 22.1(a).
(b) The pressure at a given depth in a fluid is independent of the shape of the container in which the fluid is held. In Figure 22.1(b), the pressure at X is the same as the pressure at Y.
(c) Pressure acts at right angles to the surface containing the fluid. In Figure 22.1(c), the pressures at points A to F all act at right angles to the container.
(d) When a pressure is applied to a fluid, this pressure is transmitted equally in all directions. In Figure 22.1(d), if the mass of the fluid is neglected, the pressures at points A to D are all the same.
The pressure, p, at any point in a fluid depends on three
factors:
(a) the density of the fluid, ρ, in kg/m3
(b) the gravitational acceleration, g, taken as approxi- mately 9.8 m/s2 (or the gravitational field force in N/kg), and
(c) the height of fluid vertically above the point, h metres.
The relationship connecting these quantities is:
p = ρgh pascals
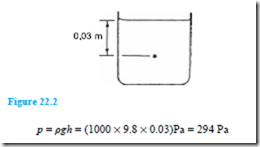
When the container shown in Figure 22.2 is filled with water of density 1000 kg/m3, the pressure due to the water at a depth of 0.03 m below the surface is given by:
In the case of the Mariana Trench, which is situated in the Pacific ocean, near Guam, the hydrostatic pressure is about 115.2 MPa or 1152 bar, where 1 bar = 105 Pa and the density of sea water being 1020 kg/m3.
Problem 4. A tank contains water to a depth of 600 mm. Calculate the water pressure (a) at a depth of 350 mm, and (b) at the base of the tank. Take the density of water as 1000 kg/m3 and the gravitational acceleration as 9.8 m/s2.
From above, pressure p at any point in a fluid is given by p = ρgh pascals, where ρ is the density in kg/m3, g is the gravitational acceleration in m/s2 and h is the height of fluid vertically above the point in metres.
(a) At a depth of 350 mm = 0.35 m,
p = ρgh = 1000 × 9.8 × 0.35
= 3430 Pa = 3.43 kPa
(b) At the base of the tank, the vertical height of the water is 600 mm = 0.6 m.
Hence, p = 1000 × 9.8 × 0.6
= 5880 Pa = 5.88 kPa
Problem 5. A storage tank contains petrol to a height of 4.7 m. If the pressure at the base of the tank is 32.2 kPa, determine the density of the petrol. Take the gravitational field force as 9.8 m/s2.
From above, pressure p = ρgh pascals, where ρ is the density in kg/m3, g is the gravitational acceleration in m/s2 and h is the vertical height of the petrol in metres.
Problem 6. A vertical tube is partly filled with mercury of density 13600 kg/m3. Find the height, in millimetres, of the column of mercury, when the pressure at the base of the tube is 101 kPa. Take the gravitational field force as 9.8 m/s2.
From above, pressure p = ρgh, hence vertical height h is given by:
That is, the height of the column of mercury is 758 mm
Now try the following Practise Exercise
Practise Exercise 117 Further problems on fluid pressure
(Take the gravitational acceleration as 9.8 m/s2)
1. Determine the pressure acting at the base of a dam, when the surface of the water is 35 m above base level. Take the density of water as 1000 kg/m3. [343 kPa]
2. An uncorked bottle is full of sea water of density 1030 kg/m3. Calculate, correct to 3 significant figures, the pressures on the side wall of the bottle at depths of (a) 30 mm, and (b) 70 mm below the top of the bottle.
[(a) 303 Pa (b) 707 Pa]
3. A U-tube manometer is used to determine the pressure at a depth of 500 mm below the free surface of a fluid. If the pressure at this depth is 6.86 kPa, calculate the density of the liquid used in the manometer. [1400 kg/m3]
4. A submarine pressure hull in the form of a circular cylinder is of external diameter 10 m and length 200 m. It dives to the bottom of the Mariana Tench which is 11.52 km deep. What will be the mass of water acting on the submarine’s circular surface in terms of the number of London double-decker buses, given that the mass of a London double-decker bus is 7 tonnes. Assume that the density of water, ρ = 1020 kg/m3 and gravitational acceleration, g = 9.81 m/s2. [10.55 million]
Atmospheric pressure
The air above the Earth’s surface is a fluid, having a density, ρ, which varies from approximately 1.225 kg/m3 at sea level to zero in outer space. Since p = ρgh, where height h is several thousands of metres, the air exerts a pressure on all points on the earth’s surface. This pressure, called atmospheric pressure, has a value of approximately 100 kilopascals (or 1 bar). Two terms are commonly used when measuring pressures:
(a) absolute pressure, meaning the pressure above that of an absolute vacuum (i.e. zero pressure), and
(b) gauge pressure, meaning the pressure above that normally present due to the atmosphere.
Thus, absolute pressure = atmospheric pressure + gauge pressure.
Thus, a gauge pressure of 50 kPa is equivalent to an absolute pressure of (100 + 50) kPa, i.e. 150 kPa, since
the atmospheric pressure is approximately 100 kPa.
Problem 7. Calculate the absolute pressure at a point on a submarine, at a depth of 30 m below the surface of the sea, when the atmospheric pressure is 101 kPa. Take the density of sea water as 1030 kg/m3 and the gravitational acceleration as 9.8 m/s2.
From Section 22.2, the pressure due to the sea, that is, the gauge pressure (pg) is given by:
Now try the following Practise Exercise
Practise Exercise 118 Further problems on atmospheric pressure
Take the gravitational acceleration as 9.8 m/s2, the density of water as 1000 kg/m3, and the density of mercury as 13600 kg/m3.
1. The height of a column of mercury in a barometer is 750 mm. Determine the atmospheric pressure, correct to 3 significant figures. [100 kPa]
2. A U-tube manometer containing mercury gives a height reading of 250 mm of mercury when connected to a gas cylinder. If the barometer reading at the same time is 756 mm of mercury, calculate the absolute pressure of the gas in the cylinder, correct to 3 significant figures. [134 kPa]
3. A water manometer connected to a condenser shows that the pressure in the condenser is 350 mm below atmospheric pressure. If the barometer is reading 760 mm of mercury, determine the absolute pressure in the condenser, correct to 3 significant figures.
[97.9 kPa]
4. A Bourdon pressure gauge shows a pressure of 1.151 MPa. If the absolute pressure is 1.25 MPa, find the atmospheric pressure in millimetres of mercury. [743 mm]