Power Supply Filter Circuits
A filter network for a high-voltage power supply typically consists of a series inductance and one or more shunt capacitances [3]. Bleeder resistors are also usually incorporated. Filter systems can be divided into two basic types:
• Inductive input, filter circuits that present a series inductance to the rectifier output.
• Capacitive input, filter circuits that present a shunt capacitance to the rectifier output.
Inductive Input Filter
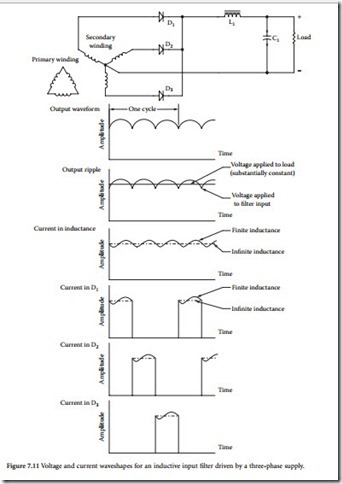
An inductive input filter is shown in Figure 7.11, along with typical current waveforms [3]. When the input inductance is infinite, current through the inductance is constant and is carried at any moment by the rectifier anode that has the most positive voltage applied to it at that instant. As the alternating volt- age being rectified passes through zero, the current suddenly transfers from one anode to another, pro- ducing square current waves through the individual rectifier devices.
When the input inductance is finite (but not too small), the situation changes to that shown by the solid lines of Figure 7.11. The current through the input inductance tends to increase when the output voltage of the rectifier exceeds the average or dc current value, and to decrease when the rectifier output voltage is less than the dc value. This causes the current through the individual anodes to be modified as shown. If the input inductance is too small, the current decreases to zero during a portion of the time between the peaks of the rectifier output voltage, and the conditions then correspond to a capacitor input filter system.
The output wave of the rectifier can be considered as consisting of a dc component upon which are superimposed ac voltages (ripple voltages). To a first approximation, the fluctuation in output current resulting from a finite input inductance can be considered as the current resulting from the lowest fre- quency component of the ripple voltage acting against the impedance of the input inductance. This assumption is permissible because the higher frequency components in the ripple voltage are smaller and at the same time encounter higher impedance. Furthermore, in practical filters, the shunting capacitor
following the input inductance has a small impedance at the ripple frequency compared with the reactance of the input inductance. The peak current resulting from a finite input inductance is, therefore, given approximately by the relation:
where
If = Peak current with finite input inductance
Ii = Peak current with infinite input inductance
E1/E0 = Ratio of lowest frequency ripple component to the dc voltage in the rectifier output
Reff = Effective load resistance
ω L1 = Reactance of the incremental value of the input inductance at the lowest ripple frequency
This equation is derived as follows:
• The peak alternating current through the input inductance is approximately E1/ω L1.
• The average or dc current is E0/Reff.
• The peak current with finite inductance is, therefore, (E1/ω L1) + (E0/Reff ).
• The current with infinite inductance is E0/Reff.
• The effective load resistance value consists of the actual load resistance plus filter resistance plus
equivalent diode and transformer resistances.
The normal operation of an inductive input filter requires that there be a continuous flow of current through the input inductance. The peak alternating current flowing through the input inductance must, therefore, be less than the dc output current of the rectifier. This condition is realized by satisfying the approximate relation
In a polyphase system, the required value of L1 is significantly less. The higher the load resistance (the lower the dc load current), the more difficult it is to maintain a continuous flow of current, and with a given L1, the previous equation will not be satisfied when the load resistance exceeds a critical value.
The minimum allowable input inductance (ω L1) is termed the critical inductance. When the inductance is less than the critical value, the filter acts as a capacitor input circuit. When the dc drawn from the rectifiers varies, it is still necessary to satisfy the ω L1 equation at all times, particularly if good voltage regulation is to be maintained. To accomplish this requirement at small load currents without excessive inductance, it is necessary to place a bleeder resistance across the output of the filter system in order to limit Reff to a value corresponding to a reasonable value of L1.
Capacitive Input Filter
When a shunt capacitance rather than a series inductance is presented to the output of a rectifier, the behavior of the circuit is greatly modified [3]. Each time the positive crest alternating voltage of the trans- former is applied to one of the rectifier anodes, the input capacitor charges up to just slightly less than
this peak voltage. The rectifier then ceases to deliver current to the filter until another anode approaches its peak positive potential, when the capacitor is charged again. During the interval when the voltage across the input capacitor is greater than the potential of any of the anodes, the voltage across the input capacitor drops off nearly linearly with time, because the first filter inductance draws a substantially con- stant current from the input capacitor. A typical set of voltage and current waves is illustrated in Figure 7.12.
The addition of a shunt capacitor to the input of a filter thus produces fundamental changes in behavior, including:
• The output voltage is appreciably higher than with an inductance input.
• The ripple voltage is lower with a capacitive input filter than an inductive input filter.
• The dc voltage across the filter input drops as the load current increases for the capacitive-input case, instead of being substantially constant, as for the inductive input case.
• The ratio of peak-to-average anode current at the rectifiers is higher in the capacitive case.
• The utilization factor of the transformer is lower with a capacitive input configuration.
Filters incorporating shunt capacitor inputs are generally employed when the amount of dc power required is small. Inductance input filters are used when the amount of power involved is large; the higher utilization factor and lower peak current result in important savings in rectifier and transformer costs under these conditions. Inductance input systems are almost universally employed in polyphase rectifier applications.