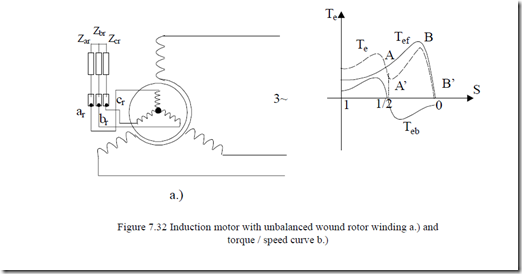
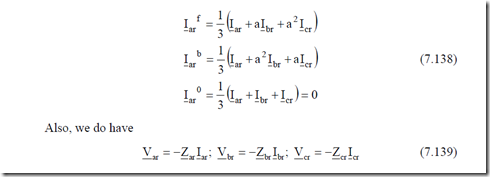Wound rotors may be provided with external three-phase resistances which may not be balanced. Also, broken bars in the rotor cage lead to unbalanced rotor windings. This latter case will be treated in Chapter 13 on transients.
However, the wound rotor unbalanced windings (Figure 7.32) may be treated here with the method of symmetrical components.
We may start decomposing the rotor phase currents Iar, Ibr and Icr into symmetrical components:
In a first approximation, all rotor currents have the frequency f2 = Sf1 at steady state. The forward mmf, produced by Iarf, Ibrf, Icrf, interacts as usual with
the stator winding and its equations are r’ R ‘If f Rrs−−VVr ‘sf = − ω= −jjSω1ψ1ψsfr; ‘ ; f ψψsf r=’f L=sL ‘Isrf I+r ‘fL+1mLI1mr ‘fIsf (7.140)
I
s
The backward mmf component of rotor currents rotates with respect to the stator at the speed n1′.
n ‘1 = n −S pf11 = pf11 (1−2S) (7.141)
So it induces stator emfs of a frequency f1′ = f1(1 – 2S). The stator may be considered short-circuited for these emfs as the power grid impedance is very small in relative terms. The equations for the backward component are rI‘ R ‘sbbRsr −= −Vrj(1’b = −− 2SjS)ωω11ψψsrb’ ; ; b ψψsbr ‘b==LL ‘sIrsbIr+’bL+1Lm1mIrI‘bsb (7.142) I
For given slip, rotor external impedances Zar, Zbr, Zcr, motor parameters stator voltage and frequency, Equation (7.139) and their counterparts for rotor voltages, (7.140) through (7.142) to determine Irf, Irb, Isf, Isb, Vr′f, Vr′b. Note that (7.140) and (7.142) are, per-phase basis and are thus valid for all three phases in the rotor and stator.
The torque expression is
Te = 3PL1 1m[Imag(Isf Ir ‘f*)+ Imag(Isb Ir ‘b*)]= Tef +Teb (7.143) The backward component torque is positive (motoring) for 1 – 2S < 0 or S > ½ and negative (braking) for S < ½. At start, the backward component torque is motoring. Also for S = ½ Isb = 0 and, thus, the backward torque is zero. This backward torque is also called monoaxial or Geörge’s torque.
The torque/speed curve obtained is given in Figure 7.33. A stable zone, AA′ around S = ½ occurs, and the motor may remain “hanged” around half ideal noload speed.
The larger the stator resistance Rs, the larger the backward torque component is. Consequently, the saddle in the torque-speed curve will be more visible in low power machines where the stator resistance is larger in relative values rs = RsIn/Vn. Moreover the frequency f1′ of stator current is close to f1 and thus visible stator backward current pulsations occur. This may be used to determine the slip S as f′ – f1 = 2Sf1. Low frequency and noise at 2Sf1 may be encountered in such cases.