LEAKAGE SATURATION INFLUENCE ON AIRGAP CONDUCTANCE

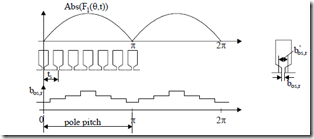
As discussed in Chapter 9, for semiopen or semiclosed stator (rotor) slots at high currents in the rotor (and stator), the teeth heads get saturated. To account for this, the slot openings are increased. Considering a sinusoidal stator mmf and only stator slotting, the slot opening increased by leakage saturation b_os′ varies with position, being maximum when the mmf is maximum (Figure 10.1).

Figure 10.1 Slot opening b_os,r variation due to slot leakage saturation

We might extract the fundamental of b_os,r(θ) function:

b’_os,r ≈ b⁰_os,r − b”_os,r cos 2( θ − ω₁t 😉 θ-electric angle (10.18)

The leakage slot saturation introduces a 2p₁ pole pair harmonic in the airgap permeance. This is translated into a variation of a₀, b₀.

a ,b_{0 0} = a ,b⁰₀ ⁰₀ − a ,b^‘₀ ^‘₀ sin(2θ−ω₁t) (10.19) a_o^o, b_o^o are the new average values of a₀(θ) and b₀(θ) with leakage saturation accounted for.

This harmonic, however, travels at synchronous speed of the fundamental wave of mmf. Its influence is notable only at high currents.

Example 10.1. Airgap conductance harmonics

Let us consider only the stator slotting with b_os/t_s = 0.2 and b_os/g = 4 which is quite a practical value, and calculate the airgap conductance harmonics.

Solution

Equations (10.13 and 10.14) are to be used with β from Table 10.1, β(4) =

0.2764,

with Kc1 ≈ ts −1.6ts βbos = 1 1.6 0.− ⋅ 12764⋅0.2 =1.097

a 0 = g1 K1_c1 = g1 1.0971 = 0.91155g

a₁ = g¹ 0.2764 _π^{4 }_0.5+ 0.78^{(1 0.2}₋^⋅ 2_⋅(⁾0.2² )2 _^sin 1.6( π⋅ ⋅1 0.2)= g¹ 0.1542

a ₂ = g¹ 0.2764 2⁴_π ^_0.5+ 0.78⁽₋^{2 0.2}2^⋅ _⋅(2 0.2⁾_⋅² )2 _^_sin 1.6( π⋅2 0.2⋅ )= g¹ 0.04886

The airgap conductance λ₁(θ) is

If for the νth harmonics the “sine” term in (10.14) is zero, so is the νth airgap conductance harmonic. This happens if

πν b^os,r = π; ν ^bos,r = 0.625

1.6

ts,r ts,r

Only the first 1, 2 harmonics are considered, so only with open slots may the above condition be approximately met.

MAIN FLUX SATURATION INFLUENCE ON AIRGAP CONDUCTANCE

In Chapter 9 an iterative analytical model (AIM) to calculate the main flux distribution accounting for magnetic saturation was introduced. Finally, we showed the way to use AIM to derive the airgap flux harmonics due to main flux path (teeth or yokes) saturation. A third harmonic was particularly visible in the airgap flux density.

As expected, this is the result of a virtual second harmonic in the airgap conductance interacting with the mmf fundamental, but it is the resultant (magnetizing) mmf and not only stator (or rotor) mmfs alone.

The two second order airgap conductance harmonics due to leakage slot flux path saturation and main flux path saturation are phase shifted as their originating mmfs are by the angle ϕ_m – ϕ₁ for the stator and ϕ _m – ϕ ₂ for the rotor. ϕ ₁, ϕ ₂, ϕ _m are the stator, rotor, magnetization mmf phase shift angle with respect to phase A axis.

λ θs ( )s = gK1 c 1+1Ks1 + 1+1Ks2 sin 2( θ − ω1t − ϕ( m − ϕ1 )) (10.20)

The saturation coefficients K_s1 and K_s2 result from the main airgap field distribution decomposition into first and third harmonics.

There should not be much influence (amplification) between the two second order saturation-caused airgap conductance harmonics unless the rotor is skewed and its rotor currents are large (> 3 to 4 times rated current), when both the skewing rotor mmf and rotor slot mmf are responsible for large main and leakage flux levels, especially toward the axial ends of stator stack. 

THE HARMONICS-RICH AIRGAP FLUX DENSITY

It has been shown [1] that, in general, the airgap flux density B_g(θ,t) is

B_g (θ,t)=µ λ_{0 1,2} ( )θ F_ν cos(νθ ω −ϕm t _ν) (10.21) where Fν is the amplitude of the mmf harmonic considered, and λ(θ) is the inversed airgap (airgap conductance) function. λ(θ) may be considered as containing harmonics due to slot openings, leakage, or main flux path saturation. However, using superposition in the presence of magnetic saturation is not correct in principle, so mere qualitative results are expected by such a method. 

THE ECCENTRICITY INFLUENCE ON AIRGAP MAGNETIC CONDUCTANCE

In rotary machines, the rotor is hardly ever located symmetrically in the airgap either due to the rotor (stator) unroundedness, bearing eccentric support, or shaft bending.

An one-sided magnetic force (uncompensated magnetic pull) is the main result of such a situation. This force tends to increase further the eccentricity, produce vibrations, noise, and increase the critical rotor speed.

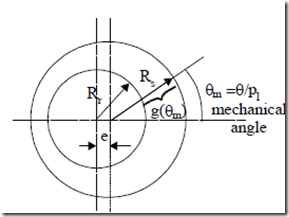
When the rotor is positioned off center to the stator bore, according to Figure 10.2, the airgap at angle θ_m is

g(θ_m )= R _s − R _r − ecosθ_m = g − ecosθ_m (10.22) where g is the average airgap (with zero eccentricity: e = 0.0).

Figure 10.2 Rotor eccentricity R_s – stator radius, R_r – rotor radius

The airgap magnetic conductance λ(θ_m) is

λ θ( m )= g(θ1m ) = g 1( − ε1cosθm ); ε = ge (10.23)

Now (10.23) may be easily decomposed into harmonics to obtain

λ θ( _m )= _g¹ (c₀ + c cos₁ θ_m +K) (10.24)

with c0 = 1 2 ; c1 = 2(c0ε−1) (10.25)

1− ε

Only the first geometrical harmonic (notice that the period here is the entire circumpherence: θ_m = θ/p₁) is hereby considered.

The eccentricity is static if the angle θ_m is a constant, that is if the rotor revolves around its axis but this axis is shifted with respect to stator axis by e.

In contrast, the eccentricity is dynamic if θ_m is dependent on rotor motion.

θm = θm − ωpr1t = θm − ω1(1p−1 S t) (10.26)

It corresponds to the case when the axis of rotor revolution coincides with the stator axis but the rotor axis of symmetry is shifted.

Now using Equation (10.21) to calculate the airgap flux density produced by the mmf fundamental as influenced only by the rotor eccentricity, static and dynamic, we obtain

Bg (θ,t)= µ0 1F cos(θ−ω1t)g1 c0 +c cos1  pθ1 −ϕs +c ‘cos1  θ−ω1p(11 −S t) −ϕd 

(10.27) As seen from (10.27) for p₁ = 1 (2 pole machines), the eccentricity produces two homopolar flux densities, B_gh(t), Bgh ( )t = µ0Fc1 1 cos(ω1t − ϕs1)++ cµh0Fc ‘g1 1 cos S( ω1t − ϕd ) (10.28) g

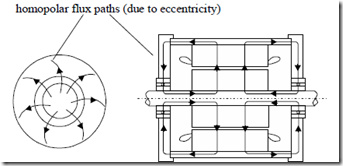
These homopolar components close their flux lines axially through the stator frame then radially through the end frame, bearings, and axially through the shaft (Figure 10.3).

The factor c_h accounts for the magnetic reluctance of axial path and end frames and may have a strong influence on the homopolar flux. For nonmagnetic frames and (or) insulated bearings c_h is large, while for magnetic steel frames, c_h is smaller. Anyway, c_h should be much larger than unity at least for the static eccentricity component because its depth of penetration (at ω₁), in the frame, bearings, and shaft, is small. For the dynamic component, c_h is expected to be smaller as the depth of penetration in iron (at Sω₁) is larger.

The d.c. homopolar flux may produce a.c. voltage along the shaft length and, consequently, shaft and bearing currents, thus contributing to bearing deterioration.

homopolar flux paths (due to eccentricity)

Figure 10.3 Homopolar flux due to rotor eccentricity

INTERACTIONS OF MMF (OR STEP) HARMONICS AND AIRGAP MAGNETIC CONDUCTANCE HARMONICS

It is now evident that various airgap flux density harmonics may be calculated using (10.21) with the airgap magnetic conductance λ_1,2(θ) either from (10.16) to account for slot openings, with a₀, b₀ from (10.19) for slot leakage saturation, or with λ_s(θ_s) from (10.20) for main flux path saturation, or λ(θ_m) from (10.24) for eccentricity.