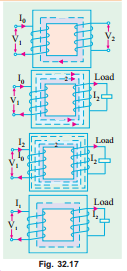
Transformer:Transformer on Load

Transformer on Load

When the secondary is loaded, the secondary current I2 is set up. The V1 magnitude and phase of I2 with respect to V 2 is determined by the characteristics of the load. Current I2 is in phase with V2 if load is non-inductive, it lags if load is inductive and it leads if load is capacitive.

The secondary current sets up its own m.m.f. (=N2I2) and hence its own flux F2 which is in opposition to the main primary flux F which  due to I0. The secondary ampere-turns N 2 I2 are known as  demagnetising amp-turns. The opposing secondary flux F2 weakensth e primary flux F momentarily, hence primary back e.m.f. E1 tends to be I reduced. For a moment V 1 gains the upper hand over E1 and hence 2 causes more current to flow in primary. I0 Let the additional primary current be I2¢. It is known as load component of primary current. This current is antiphase with I2¢. The additional primary m.m.f. N1 I2 sets up its own flux F2¢ which is in I opposition to F2 (but is in the same direction as F) and is equal to it in magnitude. Hence, the two cancel each other out. So, we find that the magnetic effects of secondary current I2 are immediately neutralized by the additional primary current I2¢ which is brought into existence exactly at the same instant as I2. The whole process is illustrated in Fig. 32.17.

Hence, whatever the load conditions, the net flux passing through the core is approximately the same as at no-load. An important deduction is that due to the constancy of core flux at all loads, the core loss is also practically the same under all load conditions.

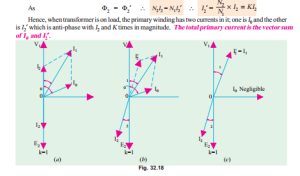
In Fig. 32.18 are shown the vector diagrams for a load transformer when load is non-inductive and when it is inductive (a similar diagram could be drawn for capacitive load). Voltage transformation ratio of unity is assumed so that primary vectors are equal to the secondary vectors. With reference to Fig. 32.18 (a), I2 is secondary current in phase with E2 (strictly speaking it should be V 2). It causes primary current I2¢ which is anti-phase with it and equal to it in magnitude (: K = 1). Total primary current I1 is the vector sum of I0 and I2¢ and lags behind V 1 by an angle f1.

In Fig. 32.18 (b) vectors are drawn for an inductive load. Here I2 lags E2 (actually V 2) by f2. Current I2¢ is again antiphase with I2 and equal to it in magnitude. As before, I1is the vector sum of I2¢ and I0 and lags behind V 1 by f1.

It will be observed that f1 is slightly greater than f2. But if we neglect I0 as compared to I2¢ as in Fig. 32.18 (c), then f1 = f2. Moreover, under this assumption

It shows that under full-load conditions, the ratio of primary and secondary currents is constant. This important relationship is made the basis of current transformer–a transformer which is used with a low-range ammeter for measuring currents in circuits where the direct connection of the ammeter is impracticable.

Example 32.12. A single-phase transformer with a ratio of 440/110-V takes a no-load current of 5A at 0.2 power factor lagging. If the secondary supplies a current of 120 A at a p.f. of 0.8 lagging, estimate the current taken by the primary.

 (Elect. Engg. Punjab Univ. 1991)

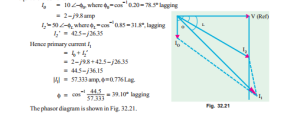
Example 32.14. A single phase transformer takes 10 A on no load at p.f. of 0.2 lagging. The turns ratio is 4 : 1 (step down). If the load on the secondary is 200 A at a p.f. of 0.85 lagging. Find the primary current and power factor.

Neglect the voltage-drop in the winding.

(Nagpur University November 1999)

Solution. Secondary load of 200 A, 0.85 lag is reflected as 50 A, 0.85 lag in terms of the primary equivalent current.

Tutorial Problems 32.2

1. The primary of a certain transformer takes 1 A at a power factor of 0.4 when it is connected across a 200-V, 50-Hz supply and the secondary is on open circuit. The number of turns on the primary is twice that on the secondary. A load taking 50 A at a lagging power factor of 0.8 is now connected across the secondary. What is now the value of primary current ?

[25.9 A]

2. The number of turns on the primary and secondary windings of a single-phase transformer are 350 and 38 respectively. If the primary winding is connected to a 2.2 kV, 50-Hz supply, determine

(a) the secondary voltage on no-load,

(b) the primary current when the secondary current is 200 A at 0.8 p.f. lagging, if the no-load current is 5 A at 0.2 p.f. lagging,

(c) the power factor of the primary current.

[239 V; 25-65 A; 0.715 lag]

3. A 400/200-V, 1-phase transformer is supplying a load of 25 A at a p.f. of 0.866 lagging. On no-load the current and power factor are 2 A and 0.208 respectively. Calculate the current taken from the supply.

 [13.9 A lagging V1 by 36.1°]

4. A transformer takes 10 A on no-load at a power factor of 0.1. The turn ratio is 4 : 1 (step down). If

a load is supplied by the secondary at 200 A and p.f. of 0.8, find the primary current and power factor (internal voltage drops in transformer are to be ignored).

 [57.2 A; 0.717 lagging]

5. A 1-phase transformer is supplied at 1,600 V on the h.v. side and has a turn ratio of 8 : 1. The transformer supplies a load of 20 kW at a power factor of 0.8 lag and takes a magnetising current of

2.0 A at a power factor of 0.2. Calculate the magnitude and phase of the current taken from the h.v. supply.

 [17.15 A ; 0.753 lag] (Elect. Engg. Calcutta Univ. 1980)

6. A 2,200/200-V, transformer takes 1 A at the H.T. side on no-load at a p.f. of 0.385 lagging. Calculate the iron losses.

If a load of 50 A at a power of 0.8 lagging is taken from the secondary of the transformer, calculate the actual primary current and its power factor.

[847 W; 5.44 A; 0.74 lag]

7. A 400/200-V, I-phase transformer is supplying a load of 50 A at a power factor of 0.866 lagging. The no-load current is 2 A at 0.208 p.f. lagging. Calculate the primary current and primary power factor.

[26.4 A; 0.838 lag] (Elect. Machines-I, Indore Univ. 1980)

Incoming search terms:

• power transformer test equipment mail
• a singke phase transformer with a ratio 440/110 takes a no load curent 5A
• the primary of a certain transformer takes 1 a at a power factor of 0 4 when connected across a 220-v 50-hz supply and the secondary is an open circuit the number of turns in the primary is twice that on the secondary
• a single phase transgormer ratio 440/110 takes a no load current of 5A at 0 2 p f
• a 1 phase transformer is supplied at 1600v on the hv side
• the no load current of a transformer in 5A at 0 3 power factor lagging and supplied at 230V 50hz The number of turns on the primary winding is 200 Calculate maximum value of flux in the core and the core losses abd magnetising current
• transformer A ; rating 100kva resistance 1% 5% transformer B ; rating 250KVA resistance 2% 2% both Tx have no load ratio of 1000/500V and are supplied from a 1000V supply Txs parallel connected calculate load on each transformer and secondary voltage
• The number of turns on the primary and secondary windings of a single-phase transfamer are are 350 and 38 respectively If the primary winding is connected to a 2 2kv 50-hz supply determine (a) the secondary voltage on no-load (b) the primary current when
• phasor diagram of transformer on load & on no load
• lagging power factor vector diagram transformer
• how find the power factor primary of a on load transformer
• Calculating magnitude of current on a single phase transformer
• draw a vector diagram of transformer on load
• capacitive load transformer phasor
• capacitive load phasor of current transformer
• find pf in step down transformer
• single phase transformer vector diagram no load primary secondary
• voltage lead or lag flux in transformer
• vector diagram for resistive & inductive load
• transformer voltage step & down and power factor
• transformer phasor diagrams
• transformer A ; rating 100kva resistance 1% 5% transformer B ; rating 250KVA resistance 2% 2% both Tx have no load ratio of 1000/500V and are supplied from a 1000V supply Txs parallel connected calculate load on each transformer and secondary voltage amA
• the primary of a certain transformer takes 1A at a power factor of 0 4 solve problem
• the primary of a certain transformer takes 1A at a power fact of 0 4 when connected across a 230V 50Hz supply
• The no load current of a single phase transformer is 5A at 0 65 pf lagging and is supplied from a 220V 50Hz supply if the primary has 400 turns calculate the core loss
• Calculate E2 of a single phase supply transformer
• A transformer takes 12A on no load at a power factor of 0 1 lagging if the load supplied by the secondary winding is 240A at power factor of 0 8 lagging and the turn ratio is 4:1 find the primary current (internal voltages dropped are negligible)
• A step down transformer has a turns ratio of 7:5 and draws a current of 10 A from the supply calculate the secondary current
• a 440/110v single phase transformer draws a no load current of 5Aat 0 2 power factor lagging if the secondary suppliesa current of 120A at a power factor of 0 8 lagging find the approximate value of the primary current
• a 440/110 single phase transformer takes a no load current of 5A at power factor 0 25 lag
• A 440/110 single phase transformer draws a no load current of 5A at 0 2 power factor lagging if the secondary supplies a current of 120A at a power factor of 0 8 lagging find the approximate value of the primary current
• a 400/200 v 50hz single phase transformer
• A 2200/200 v transformer takes 1A at H T side on no-load at a p f of 0 385 lagging Calculate the iron losses
• a 2200/200 v transformer takes 1 a at h t side on no load at a pf of 0 385 lagging calculate iron losses
• A 1-phase transformer is supplied at 1600V on the h v side and has a turn ratio 8 : 1 the transformer supplies a load of 200KW at a power factor of 0 8 lag and takes a magnetising current of 2A
• a 1 phase transformer is supplied at 1600 V on the H V side
• a 1 phase 2200/200 v transformer takes 1 A at hv side on no load at a power factor of 0 385 lag
• (b) A 2200/200V transformer takes 1A at the HT side of no-load
• a single phase 2200/200 v transformer takes 1 amp at high voltage side no load power factor 0 385 the iron loss
• A single phase 230 volts 50 hz transformer takes no load current of 5 ampear at power factor of 0 25 lagging if the primary number of turn are 200 calculate value in flux in core the core loss the magnetising current draw the vector diagram
• A single-phase transformer takes 10A on no load at pf of 0 2 lagging The turns ratio 4: 1 If the load on the secondary is 200 A at a pf 0 85 lagging find the primary current
• a single phase transformer with ratio of 440/110v take a load of current of 5A
• a single phase transformer with aratio if 440/110-V takes no load current of 5A at 0 2 power factor lagging if the secondary supplies acurrent if 120A at p f of 0 8 estimate the current taken by primary
• a single phase transformer with a ration of 440/110v takes no load
• a single phase transformer with a ratio of 440/110 takes a no load
• A single phase transformer takes 10A on no-load at p f of 0 2 lagging The turns ratio is 4:1 (step down) If the load in secondary is 200A at a p f of 0 85 lagging Find the primary current Neglect the voltage drop in the windings
• A single phase transformer has primary to secondary voltage ratio 15:1 take no load current 2A at 0 25p f lagging
• a single phase transformer has 1000turns on the primary and 200 turns on the secondary the no-load current is 3A at 0 2power
• A single phase transformer has 1000 turns on the primary and 200 turns on the secondary The no-load current is 3Amps at a power factor 0 2 lagging when the secondary current is 280amps at a power factor of 0 8 lagging calculate the primary current and pow
• 6 A 2 200/200-V transformer takes 1 A at the H T side on no-load at a p f of 0 385 lagging Calculate the iron losses If a load of 50 A at power of 0 8 lagging is taken from the secondary of the transformer calculate the actual primary current and its powe