Shift Registers and Counters part2

15·4 BINARY COUNTERS

Understanding binary counters requires some understanding of binary arithmetic, and a study of this subject is highly recom mended to those who wish to further their knowledge of complex numerical control and computer applications in industry. A brief explanation of some basic concepts of binary numbers here will suffice for an understanding of counter readout.

The decimal number system and the decade counter must utilize ten identifiable digits or conditions of the counter. This is true because there are ten numbers in the decimal system. The binary system of numbers has only two digits, 0 and 1. The decimal or decade counter must be able to indicate 10 conditions for each column or position and must have the ability to carry to the next column or position. The binary counter will only need to indicate two conditions for each column or position and have the ability to carry to the next column or position .

You may not be aware of it, but when you write a number in the decimal system such as 111, what you are actually saying is: one 100 plus one 10 plus one 1 equals 111. The positional

value of the units column is one. The positional value of the next column to the left is 10. The positional value of the next column to the left is 100, etc. Since there are nine digits possible in each column or position, the highest number possible with three positions is 999. This is actually (9 X 100) + (9 X 10) + (9 X 1).

The binary system provides only for the existence of a 1 or 0 in each position, as these are the only two digits in the system . This positional value of each column is (2.2322 2’2°). The first position’s value is 1, the second position’s value is 2, and the third position’s value is 4. Proceeding to the left, the positional values are 8, 16, 32, 64, 124, 248, etc. An easy way to remem ber this is to start with 1, and then each position to the left is the preceding position multiplied by two.

Binary numbers look a little strange until you get familiar with them. Consider the binary number 10101. This is not ten thousand one hundred one. Remember, each of the 1 digits indi cates one times the positional value of its place in the number.

The number 10101 actually says: (1 X 16) + (0 X 8) + ( 1 X 4) + (0 X 2) + (1 X 1) or 16 + 4 + 1. This of course equals 21 in decimal numbers. A little experience working with binary addition will help you get this in mind. Rememb er, when you add 0 and 0, you get 0. When you add 0 and 1, you get 1. When you add 1 and 1, you get 1 plus a carry to the next position.

Consider the MEMORYS of Fig. 15 ·12. The small circle is the ON light so that we can identify the state of the MEMORY, ON or OFF. The numbers indicate the positional va lue of the MEMORY when it is ON. Pulses fed into this group of MEMORYs are to be counted by binary arithmetic. The first pulse turns on A to indicate a one count. The second pulse turns off A and turns on B to indicate a count of two. The third pulse must turn A on and leave B on for a three count. The fourth pulse must turn off A and B and turn on C. The fifth count

will again turn on A to give a five indication. The above process continues until the maximum count of five MEMORYs, decimal number 31, is reached. The binary number 10101 or decimal ·

21 discussed previously would be displayed by A on, B off, C on, D off, E on. Numbers higher than 31 can be counted by adding MEMORY units. The addition of only one MEMORY would increase the total count to 63.

The greatest advantage to the binary counter is its economy in components. A decade counter of five elements will only count to 10, not to 31 as is possible with a binary counter.

The greatest disadvantage of the binary counter is the difficulty of readout, whether it be visual or electrical.

15.5 GENERAL ELECTRIC COMPANY BINARY COUNTER

In the binary counter, the number system used is one in which the decimal digits are represented by a binary code. This system of coding the numbers in the counter is called binary-coded decimal (BCD).

For this counter, we also use step MEMORYs. Each step MEMORY is assigned a binary code. The first unit is coded as 1 (2°); the second unit as 2 (21); the third unit as 4 (22 ); the fourth unit as 8 (23 ); and so on. The number in the counter can be read by adding the coded numbers of the units that are ON. Thus the counter for 0 to 15 will be as shown in Fig. 15·13.

If we look at the first step MEMORY (coded 1), we see that it is ON every other count. Thus the unit must change state with every step input. To do this, we connect the step MEMORY as shown in Fig. 15·14.

With this connection, the step MEMORY is steering itself ON when the unit is OFF and conversely steering itself OFF when the unit is ON. Thus, with every step input the unit will change state.

If we look at the second step MEMORY (coded 2), we see that it changes state every time the first unit turns OFF. Thus by making the connections for the second unit as shown in Fig. 15 ·14 and using the NOT output of unit 1 as the step input of unit 2, we can make a binary counter to count to 3 and reset. By chaining up step MEMORYs in the same fashion , we can make a binary counter to count to 7 with three units, to 15 with four units, to 31 with five units, and so on. With 10 step MEMORYs , the counter can count to 1,023. Figure 15·15 shows the com plete circuit for a binary counter which will count to 31.

To remove a number from a binary counter, the decode circuit consists of an AND whose number of inputs equals the number of step MEMORYs in the counter. Thus to decode a number, you must look at the state of each step MEMORY in the counter. For example, to decode the number 12 from a 0 to 31 counter you would need a five-input AND with the connections as shown in Fig. 15 ·15.

A problem exists if the output of the decode AND feeds into a module with a flip-flop circuit in it, in that the AND may have a short output pulse during the time when the step MEMORYs are switching. This is because a step MEMORY must turn off before the next step MEMORY can respond to its step input and turn on. For example, the AND shown in Fig. 15·15 may produce a pulse output on the fourteenth pulse. The thirteenth pulse would have outputs at 1, 4, and 8. The next pulse would turn the first step MEMORY off and the second unit on. Before the second unit comes on, the condition needed to read out the number 12 exists, and a very short pulse output equal to the stepping response time of the step MEMORY will occur. This problem can be taken care of by making one of the inputs to the decode AND a signal from a NOT fed by the count limit switch. Now the readout will occur after all the step MEMORYs have switched. If it is desired to read out the counter on the leading edge of the count signal, a 100 p.sec delay may be created as shown in Fig. 15 ·16. In this circuit the readout is a momentary signal ( 100 p.sec).

15 ·6 SHIFT REGISTERS

Industrial processes often require that the control system be able to keep track of where some object is as it moves through the process. The system may require the control to identify and follow several different objects at the same time and process each one differently. The control circuit for doing this is referred to as a shift register.

Suppose the problem is to identify and follow assorted material on a conveyor. Each type of material is to be taken off at a different point. The conveyor must be equipped with lugs or bins so that each type or piece of material is in a separate bin. If there are 20 bins between the input and where material A is supposed to go, a counting process is necessary to keep track of where material A is and push it off the conveyor at the correct spot, i.e., after twenty bins have passed the input point.

This process requires a stepping-type shift register. Unless the shift register is coded, a separate channel would be required for each type of material. Coding can multiply the number of types of material which can use a single channel several times.

When the process calls for a random rate of input to conveyors without lugs or bins, the sequence type of shift register is required.

We will consider only a small sample of the many possibilities for shift registers. The application of this type of control is lim ited only by the demands of the process and the ingenuity of the design engineer.

15 ·7 GENERAL ELECTRIC COMPANY SHIFT REGISTERS

The student should not be misled by the brevity or simplicity of the material presented here. The General Electric Company control system is capable of the most complex shift-register installations.

A simultaneous-type shift register is shown in Fig. 15·17. The shift-register function is conveniently accomplished with step MEMORY units. The decade counter and the ring counter, described earlier , use the shift-register connection. Figure 15·17 shows the start of a three-channel simultaneous shift-register circuit and a readout bank which may or may not be the end of the shift register.

It is advantageous to code the input because of the simplicity of decoding the output. The binary code is suggested because it is simple and easy to learn. With the three channels it is possi ble to have eight different codes. The eighth is usually the code for all channels off. For this reason only seven push buttons are shown. The outputs of these push buttons are binary coded by connecting the outputs of the original inputs together and applying this to the inputs of the step MEMORYs. OR ele ments could be used to perform this logic.

The input bank uses off-return MEMORYs since they operate with direct logic and do not need to be stepped. A step MEMORY is not recommended as the unit in the first bank because of the requirement that steering connections be present while step ping. The first shift-register bank then consists of step MEMORYS. The nth bank is shown with a number 1 and a number 7 readout AND element. The unit reset is connected to all the MEMORY units. The signal amplifier is used to step the shift register and to turn off the off-return MEMORYS.

Pressing push button 7 will turn on MEMORYS 1, 2, and 3. With these elements on, the steering networks for step MEMORYS 4, 5, and 6 are set to turn them on when the step input is applied. Closing the step limit switch will apply this step input. Now units , 4, 5, and 6 are on and units 1, 2, and 3 are off . After the nth step pulse, step MEMORYS 7, 8, and 9 will be on. AND 11 will be on, giving us the desired output.

It is possible to store n + 1 signals in the shift register at one time. This information can be stepped at an approximate maximum rate of 1,800 steps per minute. The limitation is due to the time delay in the signal amplifier or driver. The maximum rate with a controlled step input is approximately I0 kilocycles per second. A controlled step input is one which originates from a logic, since it is impossible to operate contacts at this rate and to remove the bounce effect.

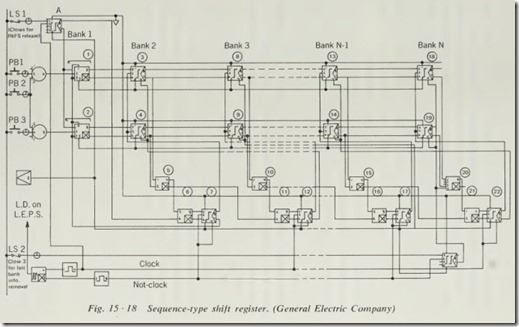
Sequence-type Shift R egister. Figure 15·18 shows the connec tions to a two-channel shift register using step MEMORYs. Shown are banks 1, 2, and 3, last bank N, and second to last bank N-1. Intermediate banks would be connected in the same way as bank 3 or N-1. The codes of both channels being off cannot be used as a signal code since it is used to tell when a bank has no information, or has been reset after having passed information on to a subsequent bank.

The sequence shift register is designed to store random input information and present this on a first-in first-out basis. This type of shift register is needed for all types of conveyors that do not have lugs to position the material being handled.

Information is shifted from one bank to the next by means of a clock pulse obtained from a sine-to-square wave converter and a pair of single shots. Where faster shifting of information is required than by the signal from the sine-to-square wave converter, other clock means may be used to shift the informa tion.

Refer to Fig. 15 ·18; there is no information in the register, and all steer connections to all MEMORYS are such that as pulses from the clock and NOT-clock signals are reaching all terminals 2s, the MEMORYS are not changing from their off condition.

In bank 1, each sealed-AND 1 and 2 has an input at terminal 1 and terminal 3. Pressing button 1, 2, or 3 will supply a third input, and the corresponding sealed AND turns on, putting in formation in bank 1 and putting the corresponding steer-on signal in the step MEMORY in bank 2. As limit switch 1 closes, a steer-on signal is put on bi-step MEMORY A. A clock signal is applied to terminal2 of bi-step MEMORY A; it turns on, supplying the final input to AND 6, which turns on to put a steer-on signal to step MEMORY 7. On the NOT-clock pulse step MEMORY 7 turns on, which pulses step MEMORY 3 and/or 4. This puts the information that was in bank 1 into bank 2. At the same time, loss of signal at terminal 7 on step MEMORY 7 resets the sealed ANDs of bank 1. At the end of the NOT-clock pulse, step MEMORY 7 is reset by loss of pulse signal at terminal 4 (terminal 7 comes

on), and the sealed ANDs 1 and 2 gain back their inputs to terminals I and 3 as soon as LSI opens and the first clock pulse turns bi-step MEMORY A off (gains output on terminal 7).

Information is now in bank 2 AND, and 5 is off, which gives an input to AND 11 and, providing there is no information in bank 3, a second input is provided to AND 11 and the steer-on signal is applied to step MEMORY 12. The first clock pulse turns on step MEMORY 12, pulsing step MEMORYS 8 and 9 so that step MEMORY 8 and/or 9 turns on and at the same time step MEMORY 12 loses the output at terminal 7, which resets bank 2 MEMORYs.

Similarly, information is transferred automatically down to the last bank. As soon as a bank has passed on information, it is reset and can then accept new information from the previous bank on the next clock or NOT-clock signal, as the case may be.

Information in the last bank is different in that it must receive its reset signal from the function being controlled . With informa tion in the last bank it may be decoded in the same way as information was decoded for the simultaneous-type shift regis ters. When the information has been used in the last bank, LS2 removes the information by closing. This puts a steer-on signal on bi-step MEMORY B, and the NOT-clock pulse turns MEMORY B on, removing the output from terminal 7, and resets bank N. Also an input from AND 20 is removed to prevent information from being shifted out of the register. As soon as LS2 opens, the first NOT-clock pulse turns bi-step MEMORY B off, returning the on signal to terminal 4 of step MEMORYs 18 and 19 and to AND 20 so that step MEMORY 22 has a steer-on signal. The first clock pulse then turns step MEMORY 22 on, which steps information into bank N and resets bank N-1.

15·8 OTHER APPLICATIONS OF STATIC CIRCUITS

The material on static control covered in this book has been limited to digital control using manufactured logic components. There are many custom designed and built static control systems, both digital and analog (feedback), which are finding wide usage in the mill-type industries.

Feedback systems sample the output in the form of voltage or current changes. These changes are then fed back into the input for a self-regulating action. This type of system is not an on-off action, such as logic control, but a modulated continu ous output controlled by feedback. One of the chief applications of feedback control is speed control of d-e motors.

Analog systems utilize the solid-state devices-transistors , diodes, and SCRs-in almost every circuit. A good foundation in solid-state electronics is fast becoming a must for anyone engaged in control work, from design to service.

Summary

Counters and shift registers are a common and growing part of control systems. Many control manufacturers have developed basic components and circuits for the most common types of counters and registers.

The wide application of binary counters and other binary equipment indicates that the control man of tomorrow will be required to know binary arithmetic and codes.

The field of static control is changing so fast that challenging new circuits of today are often made obsolete before they are in full use. The serious student of static control will develop a good foundation of fundamental concepts and then maintain a program of continued study in solid-state devices and control developments.