Problems with Digital Encoding
Quantization Noise
Although a number of ways exist by which an analogue signal can be converted into its digital equivalent, the most popular, and the technique used in the CD, is the one known as “pulse code modulation,” usually referred to as “PCM.” In this, the incoming signal is sampled at a sufficiently high repetition rate to permit the desired audio bandwidth to be achieved. In practice, this demands a sampling frequency somewhat greater than twice the required maximum audio frequency. The measured signal voltage level, at the instant of sampling, is then represented numerically as its nearest equivalent value in binary coded form (a process which is known as “quantization”).
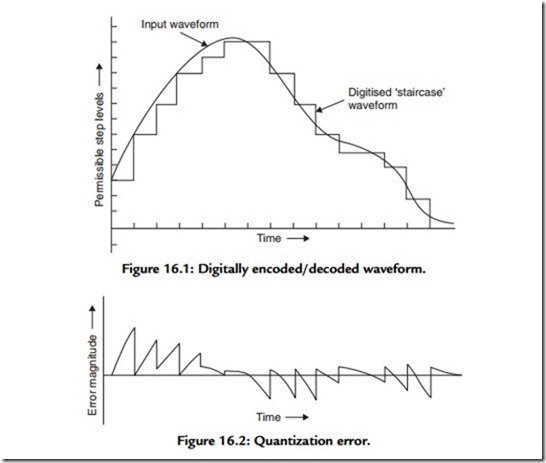
This has the effect of converting the original analogue signal, after encoding and subsequent decoding, into a voltage “staircase” of the kind shown in Figure 16.1. Obviously, the larger the number of voltage steps in which the analogue signal can be stored in digital form (that shown in the figure is encoded at “4-bit”–24 or 16 possible voltage levels), the smaller each of these steps will be and the more closely the digitally encoded waveform will approach the smooth curve of the incoming signal.
The difference between the staircase shape of the digital version and the original analogue waveform causes a defect of the kind shown in Figure 16.2, known as “quantization error,” and because this error voltage is not directly related in frequency or amplitude to the input signal, it has many of the characteristics of noise and is therefore also known as “quantization noise.” This error increases in size as the number of encoding levels is reduced. It will be audible if large enough, and is the first problem with digitally encoded
signals. I will consider this defect, and the ways by which it can be minimized, later in this chapter.
Bandwidth
The second practical problem is that of the bandwidth necessary to store or transmit such a digitally encoded signal. In the case of the CD, the specified audio bandwidth is 20 Hz to 20 kHz, which requires a sampling frequency somewhat greater than 40 kHz. In practice, a sampling frequency of 44.1 kHz is used. In order to reduce the extent of the staircase waveform quantization error, a 16-bit sampling resolution is used in the recording of the CD, equivalent to 216 or 65,536 possible voltage steps. If 16 bits are to be transmitted in each sampling interval, then, for a stereo signal, the required bandwidth will be 2 × 16 × 44100 Hz, or 1.4112 mHz, which is already 70 times greater than the audio bandwidth of the incoming signal. However, in practice, additional digital “bits” will be added to this signal for error correction and other purposes, which will extend the required bandwidth even further.
Translation Nonlinearity
The conversion of an analogue signal both into and from its binary-coded digital equivalent carries with it the problem of ensuring that the magnitudes of the binary voltage steps are defined with adequate precision. If, for example, “16-bit” encoding is used, the size of the “most significant bit” (MSB) will be 32,768 times the size of the “least significant bit” (LSB). If it is required that the error in defining the LSB shall be not worse than ±0.5%, then the accuracy demanded of the MSB must be at least within ±0.0000152% if the overall linearity of the system is not to be degraded.
The design of any switched resistor network, for encoding or decoding purposes, that demanded such a high degree of component precision would be prohibitively expensive and would suffer from great problems as a result of component aging or thermal drift. Fortunately, techniques are available that lessen the difficulty in achieving the required accuracy in the quantization steps. The latest technique, known as “low bit” or “bit-stream” decoding, side steps the problem entirely by effectively using a time-division method, since it is easier to achieve the required precision in time, rather than in voltage or current, intervals.
Detection and Correction of Transmission Errors
The very high bandwidths needed to handle or record PCM-encoded signals means that recorded data representing the signal must be very densely packed. This leads to the problem that any small blemish on the surface of the CD, such as a speck of dust, a scratch, or a thumb print, could blot out, or corrupt, a significant part of the information needed to reconstruct the original signal. Because of this, the real-life practicability of all digital record/replay systems will depend on the effectiveness of electronic techniques for the detection, correction, or, if worst comes to worst, masking of the resultant errors. Some very sophisticated systems have been devised, which are also examined later.
Filtering for Bandwidth Limitation and Signal Recovery
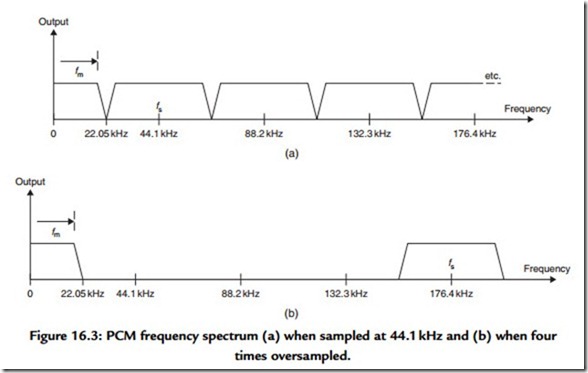
When an analogue signal is sampled and converted into its PCM-encoded digital equivalent, a spectrum of additional signals is created, of the kind shown in Figure 16.3(a), where
fs is the sampling frequency and fm is the upper modulation frequency. Because of the way in which the sampling process operates, it is not possible to distinguish between a signal having a frequency that is somewhat lower than half the sampling frequency and one that is the same distance above it; a problem called “aliasing.” In order to avoid this, it is essential to limit the bandwidth of the incoming signal to ensure that it contains no components above fs/2.
If, as is the case with the CD, the sampling frequency is 44.1 kHz and the required audio bandwidth is 20 Hz to 20 kHz, +0/-1 dB, an input “antialiasing” filter must be employed to avoid this problem. This filter must allow a signal magnitude that is close to 100% at 20 kHz, but nearly zero (in practice, usually -60 dB) at frequencies above 22.05 kHz.
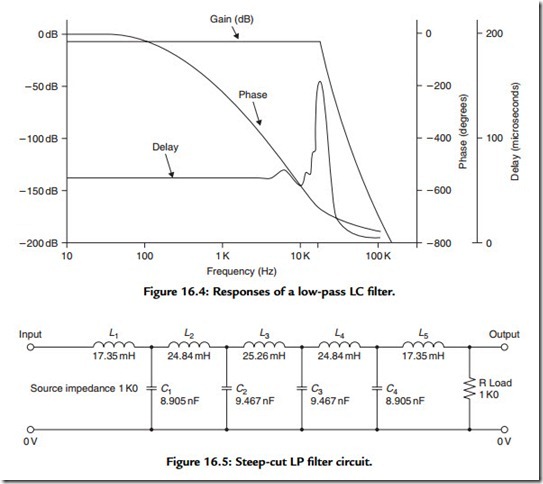
It is possible to design a steep-cut, low-pass filter that approximates closely to this characteristic using standard linear circuit techniques, but the phase shift and group delay (the extent to which signals falling within the affected band will be delayed with respect of lower frequency signals) introduced by this filter would be too large for good audio quality or stereo image presentation.
This difficulty is illustrated by the graph of Figure 16.4, which shows the relative group delay and phase shift introduced by a conventional low-pass analogue filter circuit of the kind shown in Figure 16.5. The circuit shown gives only a modest −90-dB/octave attenuation rate, while the actual slope necessary for the required antialiasing characteristics (say, 0 dB at 20 kHz and -60 dB at 22.05 kHz) would be -426 dB/octave. If a group of filters of the kind shown in Figure 16.5 were connected in series to increase the attenuation rate from -90 to -426 dB/octave, this would cause a group delay, at 20 kHz, of about 1 ms with respect to 1 kHz and a relative phase shift of some 3000°, which would be clearly audible. (In the recording equipment it is possible to employ steep-cut filter systems in which the phase and group delay characteristics are controlled more carefully than would be practicable in a mass-produced CD replay system where both size and cost must be considered.)
Similarly, because the frequency spectrum produced by a PCM-encoded 20-kHz bandwidth audio signal will look like that shown in Figure 16.3(a), it is necessary, on replay, to introduce yet another equally steep-cut low-pass filter to prevent the generation of spurious audio signals that would result from the heterodyning of signals equally disposed on either side of fs/2.
An improved performance in respect to both relative phase error and group delay in such “brick wall” filters can be obtained using so-called “digital” filters, particularly when combined with prefiltering phase correction. However, this problem was only fully solved, and then only on replay (because of the limitations imposed by the original Philips CD patents), by the use of “oversampling” techniques in which, for example, the sampling frequency is increased to 176.4 kHz (“four times oversampling”), which moves the aliasing frequency from 22.05 kHz up to 154.35 kHz, giving the spectral distribution shown in Figure 16.3(b). It is then a relatively easy matter to design a filter, such as that shown in Figure 16.14, having good phase and group delay characteristics, which has a transmission near 100% at all frequencies up to 20 kHz, but near zero at 154.35 kHz.