THE AC SINE WAVE
As the armature of the alternator is rotated through one complete revolution, a sine wave voltage is produced at its output terminals. This generated sine wave voltage varies in both voltage value and polarity.The sine wave is the most basic and widely used AC waveform. Some of the important electrical characteristics and terms used when referring to AC sine wave voltages or currents are cycle, period, and frequency.
CYCLE
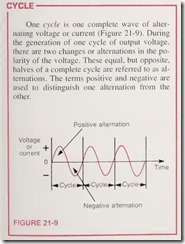
One cycle is one complete wave of alter¬ nating voltage or current (Figure 21- 9). During the generation of one cycle of output voltage, there are two changes or alternations in the polarity of the voltage. These equal, but opposite, halves of a complete cycle are referred to as alternations. The terms positive and negative are used to distinguish one alternation from the other
 PERIOD
PERIOD
The time required to produce one complete cycle is called the period of the waveform (Figure 21 -10). The period is usually measured in seconds (s) or smaller units of time such as milliseconds (ms) or microseconds (ps)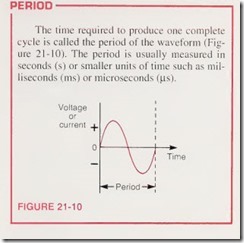
FREQUENCY
The frequency of an AC sine wave is the number of cycles produced per second (Figure 21- 11). The unit of frequency is the hertz (Hz). One hertz equals one cycle per second. For ex¬ ample. the 120 V AC electric outlet in your home has a frequency of 60 Hz. In many electronic applications, the frequen¬ cies involved are much higher. An example is your favorite radio station with a frequency of 1400 kHz. Every second that station transmits 1,400,000 complete cycles. When dealing with large quantities of cycles, prefixes are used. The more common prefixes are: K for kilo or thousand (103) M for Mega or million (10h) G for Giga or billion (104)
AC SINE WAVE VOLTAGE AND CURRENT VALUES
Since the value of a sine wave of voltage or current continually changes, you must be specific when referring to the value of the waveform you are describing. There are several ways of expressing the value of a sine wave.
PEAK VALUE
Each alternation of the sine wave is made up of a number of instantaneous values. These values are plotted at various heights above and below the horizontal line to form a continuous waveform. The peak value of a sine wave refers to the maximum voltage or current value (Figure 21 -12). Notice that two equal peak values occur during the cycle. One is during the positive alternation and the other is during the negative alternation.
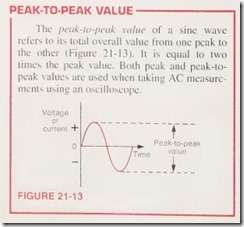
PEAK TO PEAK VALUE
The peak to peak value of a sine wave refers to its total overall value from one peak to the other (Figure 21 -13). It is equal to two times the peak value. Both peak and peak topeak values are used when taking AC measurements using an oscilloscope.
EFFECTIVE VALUE
The effective or rms value of a sine wave is the one most extensively used when referring to an AC voltage or current. It is common practice to assume that all AC voltage and current readings are effective values unless otherwise stated. Likewise, voltmeters and ammeters are calibrated to read effective (rms) values unless otherwise stated. When 1 A (ampere) of DC current flows through a resistor a certain amount of energy is dissipated by the resistor in the form of heat. An AC current that will produce the same amount of heat in the resistor is considered to have an effective current value of 1 A. Of course, the AC current must have a peak value that is higher than 1 A in order to be equivalent to a constant DC current of 1 A. In this case (Figure 12- 14), the effective value of the AC current would be 1 A, while the peak value would be approximately 1.414 A
The effective value of a sine wave of current can be determined by a mathematical process known as the root mean square, or rms method. This is the reason why the effective value is often referred to as the rms value. By using this process, it can be proven that the effective value of a sine wave of current is always equal to 0.707 times its peak value.
EXAMPLE 1
6 Assume a current sine wave has a peak value of 10 A. The effective or rms value of this current would be: 4ms = Ipeak * 0.707 /rms — (10 A)(0.707) 4ms = 7.07 A
Since an alternating current is produced by an alternating voltage, the same rule applies in terms of its effective value. The effective value of a volt¬ age sine wave is equal to 0.707 times its peak value. This equation can be transposed so that the peak value of a sine wave can be determined if its effective value is known. Accordingly, the peak value of a sine wave is equal to 1.414 times its ef¬ fective value.
EXAMPLE 2
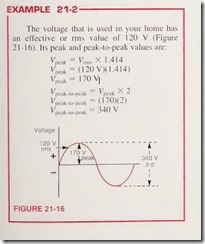
The voltage that is used in your home has an effective or rms value of 120 V (Figure 21 16). Its peak and peak to peak values are: Vpeak = Vms X 1.414 Voeak = (120V)(1.414) V, peak peak 170 V ^peak to peak Vpeak X 2 ^peak to peak = (170X2) ^peak to peak = 340 V