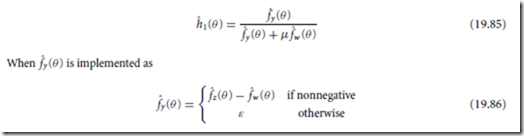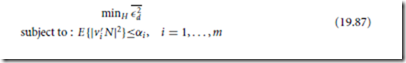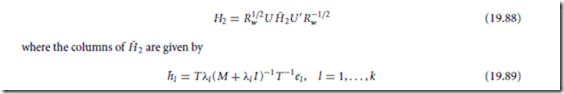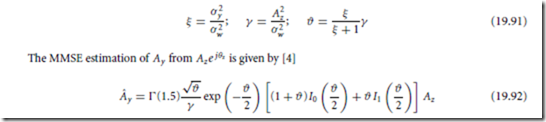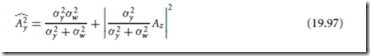19.5 A Brief Survey of Speech Enhancement2
19.5.1 Introduction
Speech enhancement aims at improving the performance of speech communication systems in noisy environments. Speech enhancement may be applied, for example, to a mobile radio communication system, a speech recognition system, a set of low quality recordings, or to improve the performance of aids for the hearing impaired. The interference source may be a wide-band noise in the form of a white or colored noise, a periodic signal such as in hum noise, room reverberations, or it can take the form of fading noise. The first two examples represent additive noise sources, while the other two examples represent convolutional and multiplicative noise sources, respectively. The speech signal may be simultaneously attacked by more than one noise source.
There are two principal perceptual criteria for measuring the performance of a speech enhancement system. The quality of the enhanced signal measures its clarity, distorted nature, and the level of residual noise in that signal. The quality is a subjective measure that is indicative of the extent to which the listener is comfortable with the enhanced signal. The second criterion measures the intelligibility of the enhanced signal. This is an objective measure which provides the percentage of words that could be correctly identified by listeners. The words in this test need not be meaningful. The two performance measures are not correlated. A signal may be of good quality and poor intelligibility and vice versa. Most speech enhancement systems improve the quality of the signal at the expense of reducing its intelligibility. Listeners can usually extract more information from the noisy signal than from the enhanced signal by careful listening to that signal. This is obvious from the data processing theorem of information theory. Listeners, however, experience fatigue over extended listening sessions, a fact that results in reduced intelligibility of the noisy signal. Is such situations, the intelligibility of the enhanced signal may be higher than that of the noisy signal. Less effort would usually be required from the listener to decode portions of the enhanced signal that correspond to high signal to noise ratio segments of the noisy signal.
Both the quality and intelligibility are elaborate and expensive to measure, since they require listening sessions with live subjects. Thus, researchers often resort to less formal listening tests to assess the quality of an enhanced signal, and they use automatic speech recognition tests to assess the intelligibility of that signal. Quality and intelligibility are also hard to quantify and express in a closed form that is amenable to mathematical optimization. Thus, the design of speech enhancement systems is often based on mathe- matical measures that are somehow believed to be correlated with the quality and intelligibility of the speech signal. A popular example involves estimation of the clean signal by minimizing the mean square error (MSE) between the logarithms of the spectra of the original and estimated signals [5]. This criterion is believed to be more perceptually meaningful than the minimization of the MSE between the original and estimated signal waveforms [13].
Another difficulty in designing efficient speech enhancement systems is the lack of explicit statistical models for the speech signal and noise process. In addition, the speech signal, and possibly also the noise process, are not strictly stationary processes. Common parametric models for speech signals, such as an autoregressive process for short-term modeling of the signal, and a hidden Markov process (HMP) for long- term modeling of the signal, have not provided adequate models for speech enhancement applications. A variant of the expectation-maximization (EM) algorithm, for maximum likelihood (ML) estimation of the autoregressive parameter from a noisy signal, was developed by Lim and Oppenheim [12] and tested in speech enhancement. Several estimation schemes, which are based on hidden Markov modeling of the clean speech signal and of the noise process, were developed over the years, see, e.g., Ephraim [6]. In each case, the HMPs for the speech signal and noise process were designed from training sequences from the two processes, respectively. While autoregressive and hidden Markov models have proved extremely useful in coding and recognition of clean speech signals, respectively, they were not found to be sufficiently refined models for speech enhancement applications.
In this chapter we review some common approaches to speech enhancement that were developed primarily for additive wide-band noise sources. Although some of these approaches have been applied to reduction of reverberation noise, we believe that the dereverberation problem requires a completely different approach that is beyond the scope of this capter. Our primary focus is on the spectral subtraction approach [13] and some of its derivatives such as the signal subspace approach [7] [11], and the estimation of the short-term spectral magnitude [16, 4, 5]. This choice is motivated by the fact that some derivatives of the spectral subtraction approach are still the best approaches available to date. These approaches are relatively simple to implement and they usually outperform more elaborate approaches which rely on parametric statistical models and training procedures.
19.5.2 The Signal Subspace Approach
In this section we present the principles of the signal subspace approach and its relations to Wiener filtering and spectral subtraction. Our presentation follows [7] and [11]. This approach assumes that the signal and noise are noncorrelated, and that their second-order statistics are available. It makes no assumptions about the distributions of the two processes.
Let Y and W be k-dimensional random vectors in a Euclidean space k representing the clean signal and noise, respectively. Assume that the expected value of each random variable is zero in an appropriately defined probability space. Let Z = Y + W denote the noisy vector. Let Ry and Rw denote the covariance matrices of the clean signal and noise process, respectively. Assume that Rw is positive definite. Let H denote a k × k real matrix in the linear space R , and let Yˆ = HZ denote the linear estimator of Y given Z. The residual signal in this estimation is given by
where I denotes, as usual, the identity matrix. To simplify notation, we shall not explicitly indicate the dimensions of the identity matrix. These dimensions should be clear from the context. In Eq. (19.78), D = (I − H)Y is the signal distortion and N = HW is the residual noise in the linear estimation. Let (·)t denote the transpose of a real matrix or the conjugate transpose of a complex matrix. Let
When H1 in Eq. (19.83) is applied to Z, it first whitens the input noise by applying R−1/2 to Z. Then, the orthogonal transformation U t corresponding to the covariance matrix of the whitened clean signal is applied, and the transformed signal is modified by a diagonal Wiener-type gain matrix.
In Eq. (19.83), components of the whitened noisy signal that contain noise only are nulled. The indices of these components are given by { j : λ j = 0}. When the noise is white, Rw = σ 2 I , and U and θ are the matrices of eigenvectors and eigenvalues of Ry /σ 2 , respectively. The existence of null components { j : λ j = 0} for the signal means that the signal lies in a subspace of the Euclidean space Rk . At the same time, the eigenvalues of the noise are all equal to σ 2 and the noise occupies the entire space k . Thus, the signal subspace approach first eliminates the noise components outside the signal subspace and then modifies the signal components inside the signal subspace in accordance with the criterion of Eq. (19.81).
When the signal and noise are wide-sense stationary, the matrices Ry and Rw are Toeplitz with associated power spectral densities of f y (θ ) and fw (θ ), respectively. The angular frequency θ lies in [0, 2π ). When the signal and noise are asymptotically weakly stationary, the matrices Ry and Rw are asymptotically To eplitz and have the associated power spectral densities f y (θ ) and fw (θ ), respectively [10]. Since the latter represents a somewhat more general situation, we proceed with asymptotically weakly stationary signal and noise.
The filter H1 in Eq. (19.82) is then asymptotically Toeplitz with associated power spectral density
This is the noncausal Wiener filter for the clean signal with an adjustable noise level determined by the constraint α in Eq. (19.81). This filter is commonly implemented using estimates of the two power spectral densities. Let fˆ (θ ) and fˆ (θ ) denote the estimates of f (θ ) and f (θ ), respectively. These estimates could, for example, be obtained from the periodogram or the smoothed periodogram. In that case, the filter is implemented as
then a spectral subtraction estimator for the clean signal results. The constant ε ≥ 0 is often referred to as a “spectral floor.” Usually µ ≥ 2 is chosen for this estimator.
The enhancement filter H could also be designed by imposing constraints on the spectrum of the residual noise. This approach enables shaping of the spectrum of the residual noise to minimize its perceptual effect.
Suppose that a set {vi , i = 1, ... , m}, m ≤ k, of k-dimensional real or complex orthonormal vectors, and a set {αi , i = 1, ... , m} of non-negative constants, are chosen. The vectors {vi } are used to transform the residual noise into the spectral domain, and the constants {αi } are used as upper bounds on the variances of these spectral components. The matrix H is obtained from
When the noise is white, the set {vi } could be the set of eigenvectors of Ry and the variances of the residual noise along these coordinate vectors are constrained. Alternatively, the set {vi } could be the set of orthonormal vectors related to the DFT. These vectors are given by v t = k−1/2(1, e− j k (i −1)·1, ... , e− j k (i −1)·(k−1)).
Here we must choose αi = αk−i +2, i = 2, ... , k/2, assuming k is even, for the residual noise power spectrum to be symmetric. This implies that at most k/2 + 1 constraints can be imposed. The DFT-related {vi } enable the use of constraints that are consistent with auditory perception of the residual noise.
To present the optimal filter, let el denote a unit vector in R for which the l th component is one and all other components are zero. Extend {v1, ... , vm} to a k × k orthogonal or unitary matrix V = (v1, ... , vk ).
Set µi = 0 for m < i ≤ k, and let M = diag(kµ1, ... , kµk ) denote the matrix of k times the Lagrange multipliers which are assumed nonnegative. Define Q = R−1/2U and T = Qt V . The optimal estimation matrix, say H = H2, is given by [11]
provided that kµi ≈= −λl for all i.l . The optimal estimator first whitens the noise, then applies the orthogonal transformation U t obtained from eigendecomposition of the covariance matrix of the whitened signal, and then modifies the resulting components using the matrix H˜ 2. This is analogous to the operation of the estimator H1 in Eq. (19.83). The matrix H˜ 2, however, is not diagonal when the input noise is colored.
When the noise is white with variance σ 2 and V = U and m = k are chosen, the optimization problem of Eq. (19.87) becomes trivial since knowledge of input and output noise variances uniquely determines the filter H. This filter is given by H = UGUt where G = diag(√α1, ... , √αk ) [7]. For this case, the heuristic choice of
where ν ≥ 1 is an experimental constant and was found useful in practice [7]. This choice is motivated by the observation that for ν = 2, the first order Taylor expansion of α−1/2 leads to an estimator H = UGUt which coincides with the Wiener estimation matrix in Eq. (19.83) with = using Eq. (19.90) performs significantly better than the Wiener filter in practice.
19.5.3 Short-Term Spectral Estimation
In another earlier approach for speech enhancement, the short-time spectral magnitude of the clean signal is estimated from the noisy signal. The speech signal and noise process are assumed statistically independent, and spectral components of each of these two processes are assumed zero mean statistically independent Gaussian random variables. Let Ay e j θy denote a spectral component of the clean signal Y in a given frame. Let Az e j θz denote the corresponding spectral component of the noisy signal. Let σ 2 = E { A2 } and σ 2 = E { A2} denote, respectively, the variances of the clean and noisy spectral components. If the variance of the corresponding spectral component of the noise process in that frame is denoted by σ 2 , then we have σ 2 = σ 2 + σ 2 . Let
where π(1.5) = √π , and I ( ) and I ( ) denote, respectively, the modified Bessel functions of the zeroth and first order. Similarly to the Wiener filter given in Eq. (19.82), this estimator requires knowledge of second order statistics of each signal and noise spectral components, σ 2 and σ 2 , respectively.
To form an estimator for the spectral component of the clean signal, the spectral magnitude estimator Eq. (19.92) is combined with an estimator of the complex exponential of that component. Let e j θy be an estimator of e j θy . This estimator is a function of the noisy spectral component Az e j θz . MMSE estimation of the complex exponential e j θy is obtained from
The constraint in Eq. (19.93) ensures that the estimator e j θy does not affect the optimality of the estimator Aˆ y when the two are combined. The constrained minimization problem in Eq. (19.93) results in the estimator 
which is simply the complex exponential of the noisy signal.
Note that the Wiener filter Eq. (19.85) has zero phase and hence it effectively uses the complex exponential of the noisy signal e j θz in estimating the clean signal spectral component. Thus, both the Wiener estimator of Eq. (19.85) and the MMSE spectral magnitude estimator of Eq. (19.92) use the complex exponential of the noisy phase. The spectral magnitude estimate of the clean signal obtained by the Wiener filter, however, is not optimal in the MMSE sense.
Other criteria for estimating Ay could also be used. For example, Ay could be estimated from
and an estimate of Ay could be obtained from
. The criterion in Eq. (19.96) aims at estimating the magnitude squared of the spectral component of the clean signal in the MMSE sense. This estimator is particularly useful when subsequent processing of the enhanced signal is performed, for example, in autoregressive analysis for low bit rate signal coding applications [13]. In that case, an estimator of the autocorrelation function of the clean signal can be obtained from the estimator 
. The optimal estimator in the sense of Eq. (19.96) is well known and is given by (see e.g., [6])
