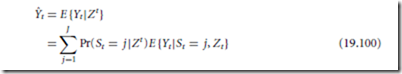19.5.1 Multiple State Speech Model
All estimators presented in Section 19.5.2 and Section 19.5.3 make the implicit assumption that the speech signal is always present in the noisy signal. In the notation of Section 19.5.2, Z = Y + W. Since the length of a frame is relatively short, in the order of 30 − 50 msec, it is more realistic to assume that speech may be present in the noisy signal with some probability, say η, and may be absent from the noisy signal with one minus that probability. Thus we have two hypotheses, one of speech presence, say H1, and the other of speech absence, say H0, that occur with probabilities η and 1 − η, respectively. We have
since E { Ay |Z, H0}= 0 and E { Ay |Z, H1}= Aˆy as given by Eq. (19.92). The more realistic estimator given in Eq. (19.99) was found useful in practice as it improved the performance of the estimator in Eq. (19.92). Other estimators may be derived under this model. Note that the model as in Eq. (19.98) is not applicable to the estimator in Eq. (19.95) since Ay must be positive for the criterion in Eq. (19.94) to be meaningful. Speech enhancement under the speech presence uncertainty model was first proposed and applied by McAulay and Malpass in their pioneering work [16].
An extension of this model leads to the assumption that speech vectors may be in different states at different time instants. The speech presence uncertainty model assumes two states representing speech presence and speech absence. In another model of Drucker [3], five states were proposed representing fricative, stop, vowel, glide, and nasal speech sounds. A speech absence state could be added to that model as a sixth state. This model requires an estimator for each state just as in Eq. (19.99).
A further extension of these ideas, in which multiple states that evolve in time are possible, is obtained when one models the speech signal by a hidden Markov process (HMP) [8]. An HMP is a bivariate random process of states and observations sequences. The state process {St , t = 1, 2, .. .} is a finite-state homogeneous Markov chain that is not directly observed. The observation process {Yt , t = 1, 2, .. .} is conditionally independent given the state process. Thus, each observation depends statistically only on the state of the Markov chain at the same time and not on any other states or observations. Consider, for example, an HMP observed in an additive white noise process {Wt , t = 1, 2, .. .}. For each t, let Zt = Yt + Wt denote the noisy signal. Let Zt = {Z1, ... , Zt }. Let J denote the number of states of the Markov chain. The causal MMSE estimator of Yt given {Zt } is given by [6]
The estimator as given in Eq. (19.100) reduces to Eq. (19.99) when J = 2 and Pr(St = j |Zt ) = Pr(St = j |Zt ), or when the states are statistically independent of each other.
An HMP is a parametric process that depends on the initial distribution and transition matrix of the Markov chain and on the parameter of the conditional distributions of observations given states. The parameter of an HMP can be estimated off-line from training data and then used in constructing the estimator in Eq. (19.100). This approach has a great theoretical appeal since it provides a solid statistical model for speech signals. It also enjoys a great intuitive appeal since speech signals do cluster into sound groups of distinct nature, and dedication of a filter for each group is appropriate. The difficulty in implementing this approach is in achieving low probability of error in mapping vectors of the noisy speech onto states of the HMP. Decoding errors result in wrong association of speech vectors with the set of predesigned estimators {E {Yt |St = j, Zt }, j = 1, ... , J }, and thus in poorly filtered speech vectors. In addition, the complexity of the approach grows with the number of states, since each vector of the signal must be processed by all J filters.
The approach outlined above could be applied based on other models for the speech signal. For example, in [20], a harmonic process based on an estimated pitch period was used to model the speech signal.
19.5.2 Second-Order Statistics Estimation
Each of the estimators presented in Section 19.5.2 and Section 19.5.3 depends on some statistics of the clean signal and noise process which are assumed known a–priori. The signal subspace estimators as in Eq. (19.82) and Eq. (19.88) require knowledge of the covariance matrices of the signal and noise. The spectral magnitude estimators in Eq. (19.92), Eq. (19.95), and Eq. (19.97) require knowledge of the variance of each spectral component of the speech signal and of the noise process. In the absence of explicit knowledge of the second-order statistics of the clean signal and noise process, these statistics must be estimated either from training sequences or directly from the noisy signal.
We note that when estimates of the second-order statistics of the signal and noise replace the true second- order statistics in a given estimation scheme, the optimality of that scheme can no longer be guaranteed. The quality of the estimates of these second-order statistics is key for the overall performance of the speech enhancement system. Estimation of the second-order statistics can be performed in various ways usually outlined in the theory of spectral estimation [19]. Some of these approaches are reviewed in this section. Estimation of speech signals second-order statistics from training data has proven successful in coding and recognition of clean speech signals. This is commonly done in coding applications using vector quantization and in recognition applications using hidden Markov modeling. When only noisy signals are available, however, matching of a given speech frame to a codeword of a vector quantizer or to a state of an HMP is susceptible to decoding errors. The significance of these errors is the creation of a mismatch between the true and estimated second order statistics of the signal. This mismatch results in application of wrong filters to frames of the noisy speech signal, and in unacceptable quality of the processed noisy signal. On-line estimation of the second-order statistics of a speech signal from a sample function of the noisy signal has proven to be a better choice. Since the analysis frame length is usually relatively small, the covariance matrices of the speech signal may be assumed Toeplitz. Thus, the autocorrelation function of the clean signal in each analysis frame must be estimated. The Fourier transform of a windowed autocorrelation function estimate provides estimates of the variances of the clean signal spectral components.
For a wide-sense stationary noise process, the noise autocorrelation function can be estimated from an initial segment of the noisy signal that contains noise only. If the noise process is not wide-sense stationary, frames of the noisy signal must be classified as in Eq. (19.98), and the autocorrelation function of the noise process must be updated whenever a new noise frame is detected.
In the signal subspace approach [7], the power spectral densities of the noise and noisy processes are first estimated using windowed autocorrelation function estimates. Then, the power spectral density of the clean signal is estimated using Eq. (19.86). That estimate is inverse Fourier transformed to produce an estimate of the desired autocorrelation function of the clean signal. In implementing the MMSE spectral estimator as in Eq. (19.92), a recursive estimator for the variance of each spectral component of the clean signal developed in [4] is often used, see, e.g., [1, 2]. Let Aˆ y (t) denote an estimator of the magnitude of a spectral component of the clean signal in a frame at time t. This estimator may be the MMSE estimator as in Eq. (19.92). Let Az (t) denote the magnitude of the corresponding spectral component of the noisy signal. Let σ�2 (t) denote the estimated variance of the spectral component of the noise process in that frame. Let σ�2(t) denote the estimated variance of the spectral component of the clean signal in that frame. This estimator is given by
where 0 ≤ β ≤ 1 is an experimental constant. We note that while this estimator was found useful in practice, it is heuristically motivated and its analytical performance is not known.
A parametric approach for estimating the power spectral density of the speech signal from a given sample function of the noisy signal was developed by Musicus and Lim [18]. The clean signal in a given frame is assumed a zero mean Gaussian autoregressive process. The noise is assumed a zero mean white Gaussian process that is independent of the signal. The parameter of the noisy signal comprises the autoregressive coefficients, the gain of the autoregressive process, and the variance of the noise process. This parameter is estimated in the ML sense using the EM algorithm. The EM algorithm and conditions for its convergence were originally developed for this problem by Musicus [17]. The approach starts with an initial estimate of the parameter. This estimate is used to calculate the conditional mean estimates of the clean signal and of the sample covariance matrix of the clean signal given the noisy signal. These estimates are then used to produce a new parameter, and the process is repeated until a fixed point is reached or a stopping criterion is met.
This EM procedure is summarized as follows: Consider a scalar autoregressive process {Yt , t = 1, 2, .. .}
of order r and coefficients a = (a1, ... , ar )t. Let {Vt } denote an independent identically distributed sequence of zero mean unit variance Gaussian random variables. Let σv denote a gain factor. A sample function of the autoregressive process is given by
Assume that the initial conditions of Eq. (19.102) are zero, i.e., yt = 0 for t < 1. Let {Wt , t = 1, 2, .. .} denote the noise process which comprises an iid sequence of zero mean unit variance Gaussian random variables. Consider a k-dimensional vector of the noisy autoregressive process. Let Y = (Y1, ... , Yk )t, and define similarly the vectors V and W corresponding to the processes {Vt } and {Wt }, respectively. Let A denote a lower triangular Toeplitz matrix with the first column given by (1, a1, ... , ar , 0, ... , 0)t. Then
Suppose φm = (a(m), σv (m), σw (m)) denotes an estimate of the parameter of Z at the end of the mth iteration. Let A(m) denote the matrix A constructed from the vector a(m). Let Ry (m) = σ 2(m) A(m)−1(A(m))−1)t denote the covariance matrix of the autoregressive process of Eq. (19.102) as obtained from . Let Rz (m) = Ry (m) + σ 2 (m)I denote the covariance matrix of the noisy signal as shown in Eq. (19.103) based on φm. Let Yˆ and Rˆ denote, respectively, the conditional mean estimates of the clean signal Y and of the sample covariance of Y given Z and the current estimate φm. Under the Gaussian assumptions of this problem, we have
The calculation of the parameter of the noisy signal in Eq. (19.107) to Eq. (19.109) comprise the M-step of the EM algorithm.
Note that the enhanced signal can be obtained as a by-product of this algorithm using the estimator as in Eq. (19.104) at the last iteration of the algorithm. Formulation of the above parameter estimation problem in a state space assuming colored noise in the form of another autoregressive process, and implementation of the estimators as given in Eq. (19.104) and Eq. (19.105) using Kalman filtering and smoothing was done in [9].
The EM approach presented above differs from an earlier approach pioneered by Lim and Oppenheim [12]. Assume for this comparison that the noise variance is known. In the EM approach, the goal is to derive the ML estimate of the true parameter of the autoregressive process. This is done by local maximization of the likelihood function of the noisy signal over the parameter set of the process. The EM approach results in alternate estimation of the clean signal Y and its sample correlation matrix YY t, and of the parameter of the autoregressive process (a, σv ). The approach taken in [12] aims at estimating the parameter of the autoregressive process that maximizes the joint likelihood function of the clean and noisy signals. Using alternate maximization of the joint likelihood function, the approach resulted in alternate estimation of the clean signal Y and of the parameter of the autoregressive process (a, σv ). Thus, the main difference between the two approaches is in the estimated statistics from which the autoregressive parameter is estimated in each iteration. This difference impacts the convergence properties of the algorithm [12] which is known to produce an inconsistent parameter estimate. The algorithm [12] is simpler to implement than the EM approach and it is popular among some authors. To overcome the inconsistency, they developed a set of constraints for the parameter estimate in each iteration.
19.5.3 Concluding Remarks
We have surveyed some aspects of the speech enhancement problem and presented state-of-the-art solutions to this problem. In particular, we have identified the difficulties inherent to speech enhancement, and presented statistical models and distortion measures commonly used in designing estimators for the clean signal. We have mainly focused on speech signals degraded by additive noncorrelated wide-band noise. As we have noted earlier, even for this case, a universally accepted solution is not available and more research is required to refine current approaches or alternatively develop new ones. Other noise sources, such as room reverberation noise, present a more significant challenge as the noise is a non-stationary process that is correlated with the signal and it cannot be easily modeled. The speech enhancement problem is expected to attract significant research effort in the future due to challenges that this problem poses, the numerous potential applications, and future advances in computing devices.
References
1. Cappe´, O., Elimination of the musical noise phenomenon with the Ephraim and Malah noise suppressor, IEEE Trans. Speech and Audio Proc., vol. 2, pp. 345–349, Apr. 1994.
2. Cohen, I. and Berdugo, B.H., Speech enhancement for non-stationary noise environments, Signal Processing, vol. 81, pp. 2403–2418, 2001.
3. Drucker, H., Speech processing in a high ambient noise environment, IEEE Trans. Audio Electroacoust., vol. AU-16, pp. 165–168, Jun. 1968.
4. Ephraim, Y. and Malah, D., Speech enhancement using a minimum mean square error short time spectral amplitude estimator, IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-32, pp. 1109– 1121, Dec. 1984.
5. Ephraim Y. and Malah, D., Speech enhancement using a minimum mean square error Log-spectral am- plitude estimator, IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-33, pp. 443–445, Apr. 1985.
6. Ephraim, Y., Statistical model based speech enhancement systems, Proc. IEEE, vol. 80, pp. 1526–1555, Oct. 1992.
7. Ephraim, Y. and Van Trees, H.L., A signal subspace approach for speech enhancement, IEEE Trans.
Speech and Audio Proc., vol. 3, pp. 251–266, July 1995.
8. Ephraim, Y. and Merhav, N., Hidden Markov Processes, IEEE Trans. Inform. Theory, vol. 48, pp. 1518–1569, June 2002.
9. Gannot, S., Burshtein, D., and Weinstein, E., Iterative and sequential Kalman filter-based speech enhancement algorithms, IEEE Trans. Speech and Audio Proc., vol. 6, pp. 373–385, July 1998.
10. Gray, R.M., Toeplitz and Circulant Matrices: II. Stanford Electron. Lab., Tech. Rep. 6504–1, Apr. 1977.
11. Lev-Ari, H. and Ephraim, Y., Extension of the signal subspace speech enhancement approach to
colored noise, IEEE Sig. Proc. Let., vol. 10, pp. 104–106, Apr. 2003.
12. Lim, J.S. and Oppenheim, A.V., All-pole modeling of degraded speech, IEEE Trans. Acoust., Speech,
Signal Processing, vol. ASSP–26, pp. 197–210, June 1978.
13. Lim J.S. and Oppenheim, A.V., Enhancement and bandwidth compression of noisy speech, Proc.
IEEE, vol. 67, pp. 1586–1604, Dec. 1979.
14. Lim, J.S., ed., Speech Enhancement. Prentice-Hall, New Jersey, 1983.
15. Makhoul, J., Crystal, T.H., Green, D.M., Hogan, D., McAulay, R.J., Pisoni, D.B., Sorkin, R.D., and
Stockham, T.G., Removal of Noise From Noise-Degraded Speech Signals. Panel on removal of noise
from a speech/noise National Research Council, National Academy Press, Washington, D.C., 1989.
16. McAulay, R.J. and Malpass, M.L., Speech enhancement using a soft-decision noise suppression filter,
IEEE Trans. Acoust., Speech, Signal Processing, ASSP-28, pp. 137–145, Apr. 1980.
17. Musicus, B.R., An Iterative Technique for Maximum Likelihood Parameter Estimation on Noisy Data.
Thesis, S.M., M.I.T., Cambridge, MA, 1979.
18. Musicus, B.R. and Lim, J.S., Maximum likelihood parameter estimation of noisy data, Proc. IEEE Int.
Conf. on Acoust., Speech, Signal Processing, pp. 224–227, 1979.
19. Priestley, M.B., Spectral Analysis and Time Series, Academic Press, London, 1989.
20. Quatieri, T.F. and McAulay, R.J., Noise reduction using a soft-decision sin-wave vector quantizer,
IEEE Int. Conf. Acoust., Speech, Signal Processing, pp. 821–824, 1990.
Defining Terms
Speech Enhancement: The action of improving perceptual aspects of a given sample of speech signals.
Quality: A subjective measure of the way a speech signal is perceived.
Intelligibility: An objective measure which indicates the percentage of words from a given text that are expected to be correctly understood by listeners.
Signal estimator: A function of the observed noisy signal which approximates the clean signal.
Expectation-maximization: An iterative approach for parameter estimation using alternate estimation and maximization steps.
Autoregressive process: A random process obtained by passing white noise through an all-pole filter.
Wide-sense stationarity: A property of a random process whose second-order statistics do not change with time.
Asymptotically weakly stationarity: A property of a random process indicating eventual wide-sense stationarity.
Hidden Markov Process: A Markov chain observed through a noisy channel.