Memory, I/O, and Parallel Processing : following example.

Example 8.2

Assume the following values for the system of Figure 8.14:

• Length of the virtual address field =32 bits
• Length of the segment number field = 12 bits
• Length of the page number field = 8 bits
• Length of the displacement field = 12 bits

Now, determine the value of the physical address using the following information:

• Value of the virtual address field=000FA0BA ₁₆
• Contents of the segment table address (000) ₁₆ = OFF₁₆
• Contents of the page table address (IF9₁₆) = AC ₁₆

Solution

From the given virtual address, the segment table address is 00016 (three high-order hexadecimal digits of the virtual address). It is given that the contents of this segment-able address is OFF _16• Therefore, by adding the page number p (fourth and fifth hexadecimal digits of the virtual address) with OFF 16,the base address of the page table can be determined as:

0FF ₁₆ + FA ₁₆ = 1F9₁₆

Since the contents of the page table address 1F916 is AC 16, the physical address can be obtained by adding the displacement (low-order three hexadecimal digits of the virtual address) with AC 16 as follows:

AC000 ₁₆ + 000BA ₁₆ = AC0BA ₁₆

In this addition, the displacement value 0BA is sign-extended to obtain a 20-bit number that can be directly added to the base value p’. The same final answer can be obtained if p’

and dare first concatenated. Thus, the value of the physical address is ACOBA _16• The virtual space of some computers use both paging and segmentation, and it is called a linear segmented virtual memory system. In this system, the main memory is accessed three times to retrieve data (one for accessing the page table; one for accessing the segment table; and one for accessing the data itself).

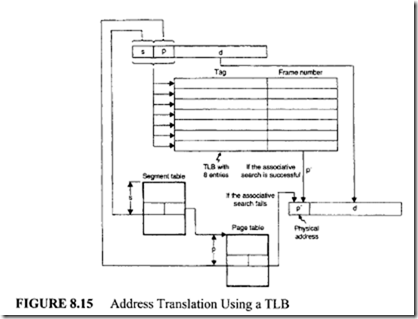
Accessing the main memory is a time-consuming operation. To speed up the retrieval operation, a small associative memory ( implemented as an on-chip hardware in modem microprocessors) called the translation lookaside buffer (TLB) is used. The TLB stores the translation information for the 8 or 16 most recent virtual addresses. The organization of a address translation scheme that includes a TLB is shown in Figure 8.15.

In this scheme, assume the TLB is capable of holding the translation information about the 8 most recent virtual addresses.

The pair (s, p) of the virtual address is known as a tag, and each entry in the TLB is of the form:

When a user program generates a virtual address, the (s, p) pair is associatively compared with all tags held in the TLB for a match. Ifthere is a match, the physical address is formed by retrieving the base address of the frame p’ from the TLB and concatenating this with the displacement d. However, in the event of a TLB miss, the physical address is generated after accessing the segment and page tables, and this information will also be loaded in the TLB. This ensures that translation information pertaining to a future reference is confined to the TLB. To illustrate the effectiveness of the TLB, the following numerical example is provided.

Example 8.3

The following measurements are obtained from a computer system that uses a linear segmented memory system with a TLB:

• Number of entries in the TLB = 16
• Time taken to conduct an associative search in the TLB = 160 ns
• Main memory access time = 1 _μS

Determine the average access time assuming a TLB hit ratio of 0.75.

Solution

In the event of a TLB hit, the time needed to retrieve the data is:

This example shows that the use of a small TLB significantly improves the efficiency of the retrieval operation (by 33%). There are two main reasons for this improvement. First, the TLB is designed using the associated memory. Second, the TLB hit ratio may be attributed to the locality of reference. Simulation studies indicate that it is possible to achieve a hit ratio in the range of 0.8 to 0.9 by having a TLB with 8 to 16 entries.

In a computer based on a linear segmented virtual memory system, the performance parameters such as storage use are significantly influenced by the page size p. For instance, when p is very large, excessive internal fragmentation will occur. If p is small, the size of the page table becomes large. This results in poor use of valuable memory space. The selection of the page size p is often a compromise. Different computer systems use different page sizes. In the following, important memory-management strategies are described. There are three major strategies associated with the management:

• Fetch strategies
• Placement strategies
• Replacement strategies

All these strategies are governed by a set of policies conceived intuitively. Then they are validated using rigorous mathematical methods or by conducting a series of simulation experiments. A policy is implemented using some mechanism such as hardware, software, or firmware.

Fetch strategies deal with when to move the next page to main memory. Recall that when a page needed by a program is not in the main memory, a page fault occurs. In the event of a page fault, the page-fault handler will read the required page from the secondary memory and enter its new physical memory location in the page table, and the instruction execution continues as though nothing has happened.

In a virtual memory system, it is possible to run a program without having any page in the primary memory. In this case, when the first instruction is attempted, there is a page fault. As a consequence, the required page is brought into the main memory, where the instruction execution process is repeated again. Similarly, the next instruction may also cause a page fault. This situation is handled exactly in the same manner as described before. This strategy is referred to as demand paging because a page is brought in only when it is needed. This idea is useful in a multiprogramming environment because several programs can be kept in the main memory and executed concurrently.

However, this concept does not give best results if the page fault occurs repeatedly. For instance, after a page fault, the page- fault handler has to spend a considerable amount of time to bring the required page from the secondary memory. Typically, in a demand paging system, the effective access time tav is the sum of the main memory access time t and μ, where J1 is the time taken to service a page fault. Example 8.4 illustrates the concept.

Example 8.4

(a) Assuming that the probability of a page fault occurring is p, derive an expression for tav in terms oft, μ , and p.

(b)  Suppose that t = 500 ns and μ= 30 ms, calculate the effective access time tav if it is given that on the average, one out of 200 references results in a page fault.

Solution

(a) If a page fault does not occur, then the desired data can be accessed within a time t. (From the hypothesis the probability for a page fault not to occur is 1 –p). If the page fault occurs, then μ time units are required to access the data. The effective access time is

l_av = ( 1 – P)t +Pμ

(b) Since it is given that one out of every 200 references generates a page fault, p = 1/200. Using the result derived in part (a):

l_av = ((1- 0.005) X 0.5 + 0.005 X 30,000) μ S

= (0.995 X 0.5 + 150) μ S = [0.4975 + 150) μ S

= 150.4975 μ S

These parameters have a significant impact on the performance of a time-sharing system.

As an alternative approach, anticipatory fetching can be adapted. This conclusion is based on the fact that in a short period of time addresses referenced by a program are

clustered around a particular region of the address space. This property is known as locality of reference.

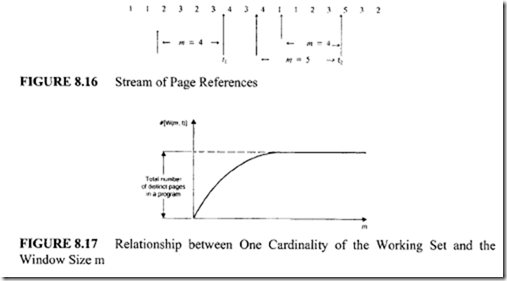
The working set of a program W(m, t) is defined as the set of m most recently needed pages by the program at some instant of time t. The parameter m is called the window of the working set. For example, consider the stream of references shown in Figure 8.16:

From this figure, determine that:

In general, the cardinality of the set W(O, t) is zero, and the cardinality of the set W(oo, t) is equal to the total number of distinct pages in the program. Since m + 1 most-recent page references include m most-recent page references:

#[W(m + 1, t)] #[W(m, t)]

In this equation, the symbol# is used to indicate the cardinality of the set W(m, t). When m is varied from 0 to=, #W(m, t) increases exponentially. The relationship between m and #W(m, t) is shown in Figure 8.17.

In practice, the working set of program varies slowly with respect to time. Therefore, the working set of a program can be predicted ahead of time. For example, in a multiprogramming system, when the execution of a suspended program is resumed, its present working set can be reasonably estimated based on the value of its working set at the time it was suspended. If this estimated working set is loaded, page faults are less likely to occur. This anticipatory fetching further improves the system performance because the working set of a program can be loaded while another program is being executed by the CPU. However, the accuracy of a working set model depends on the value of m. Larger values of m result in more-accurate predictions. Typical values of m lie in the range of 5000 to 10,000.

To keep track of the working set of a program, the operating system has to perform time-consuming housekeeping operations. This activity is pure overhead, and thus the system performance may be degraded.

Placement strategies are significant with segmentation systems, and they are concerned with where to place an incoming program or data in the main memory. The following are the three widely used placement strategies:

• First-fit technique
• Best-fit technique
• Worst-fit technique

The first-fit technique places the program in the first available free block or hole that is adequate to store it. The best-fit technique stores the program in the smallest free hole of all the available holes able to store it. The worst-fit technique stores the program in the largest free hole. The first-fit technique is easy to implement and does not have to scan the entire space to place a program. The best-fit technique appears to be efficient because it finds an optimal hole size. However, it has the following drawbacks:

• It is very difficult to implement.
• It may have to scan the entire free space to find the smallest free hole that can hold the incoming program. Therefore, it may be time-consuming.
• It has the tendency continuously to divide the holes into smaller sizes. These smaller holes may eventually become useless.

Worst-fit strategy is sometimes used when the design goal is to avoid creating small holes. In general, the operating system maintains a list known as the available space list (ASL) to indicate the free memory space. Typically, each entry in this list includes the following information:

• Starting address of the free block
• Size of the free block

After each allocation or release, the operating system updates the ASL. In the following example, the mechanics of the various placement strategies presented earlier are explained.

Example 8.5

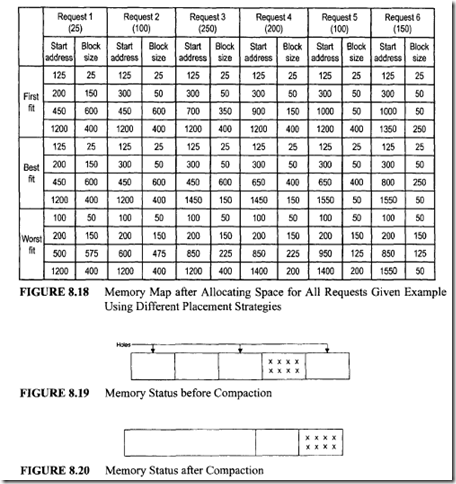
The available space list of a computer memory system is specified as follows:

Solution

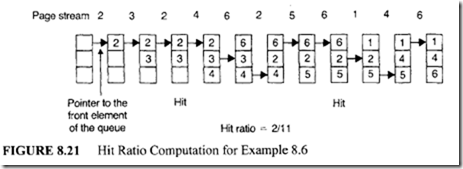
a) First-fit method. Consider the first request with a block size of25. Examination of the block sizes of the available space list reveals that this request can be satisfied by allocating from the first available block. The block size (50) is the first of the available space list and is adequate to hold the request (25 blocks). Therefore, the first request with 25 blocks will be allocated from the available space list starting at address 100 with a block size of 50. Request 1 will be allocated starting at an address of I 00 ending at an address 100 + 24 = 124 (25 locations including 100). Therefore, the first block of the available space list will start at 125 with a block size of 25. The starting address and block size of each request can be calculated similarly.

b) Best-fit method. Consider request 1. Examination of the available block size reveals that this request can be satisfied by allocating from the first smallest available block capable of holding it. Request 1 will be allocated starting at address 100 and ending at 124. Therefore, the available space list will start at 125 with a block size of25.

c) Worst-fit method. Consider request I. Examination of the available block sizes reveals that this request can be satisfied by allocating from the third block (largest) starting at 450. After this allocation the starting address of the available list will be 500 instead of 450 with a block size of600- 25 = 575. Various results for all the other requests are shown in Figure 8.18.

In a multiprogramming system, programs of different sizes may reside in the main memory. As these programs are completed, the allocated memory space becomes free. It may happen that these unused free spaces, or holes, become available between two allocated blocks, or partitions. Some of these holes may not be large enough to satisfY the memory request of a program waiting to run. Thus valuable memory space may be wasted. One way to get around this problem is to combine adjacent free holes to make the hole size larger and usable by other jobs. This technique is known as coalescing of holes.

It is possible that the memory request made by a program may be larger than

any free hole but smaller than the combined total of all available holes. If the free holes are combined into one single hole, the request can be satisfied. This technique is known as memory compaction. For example, the status of a computer memory before and after memory compaction is shown in Figures 8.19 and 8.20, respectively.

Placement strategies such as first-fit and best-fit are usually implemented as software procedures. These procedures are included in the operating system’s software. The advent ofhigh-levellanguages such as Pascal and C greatly simplify the programming effort because they support abstract data objects such as pointers. The available space list discussed in this section can easily be implemented using pointers.

The memory compaction task is perfonned by a special software routine of the operating system called a garbage collector. Nonnally, an operating system runs the garbage collector routine at regular intervals.

In a paged virtual memory system, when no frames are vacant, it is necessary

to replace a current main memory page to provide room for a newly fetched page. The page for replacement is selected using some replacement policy. An operating system implements the chosen replacement policy. In general, a replacement policy is considered efficient if it guarantees a high hit ratio. The hit ratio h is defined as the ratio of the number of page references that did not cause a page fault to the total number of page references.

The simplest of all page replacement policies is the FIFO policy. This algorithm selects the oldest page (or the page that arrived first) in the main memory for replacement. The hit ratio h for this algorithm can be analytically determined using some arbitrary stream of page references as illustrated in the following example.

Example 8.6

Consider the following stream of page requests.

2, 3, 2, 4, 6, 2, 5, 6, 1, 4, 6

Determine the hit ratio h for this stream using the FIFO replacement policy. Assume the main memory can hold 3 page frames and initially all of them are vacant.

Solution

The hit ratio computation for this situation is illustrated in Figure 8.21.

From Figure 8.21, it can be seen that the first two page references cause page faults. However, there is a hit with the third reference because the required page (page 2) is already in the main memory. After the first four references, all main memory frames are completely used. In the fifth reference, page 6 is required. Since this page is not in the main memory, a page fault occurs. Therefore, page 6 is fetched from the secondary memory. Since there are no vacant frames in the main memory, the oldest of the current main memory pages is selected for replacement. Page 6 is loaded in this position. All other data tabulated in this figure are obtained in the same manner. Since 9 out of 11 references generate a page fault, the hit ratio is 2/11.

The primary advantage of the FIFO algorithm is its simplicity. This algorithm can be implemented by using a FIFO queue. FIFO policy gives the best result when page references are made in a strictly sequential order. However, this algorithm fails if a program loop needs a variable introduced at the beginning. Another difficulty with the FIFO algorithm is it may give anomalous results.

Intuitively, one may feel that an increase in the number of page frames will also increase the hit ratio. However, with FIFO, it is possible that when the page frames are increased, there is a drop in the hit ratio. Consider the following stream of requests:

1,2,3,4,5, 1,2,5, 1,2,3,4,5,6,5

Assume the main memory has 4 page frames; then using the FIFO policy there is a hit ratio of 4/15. However, if the entire computation is repeated using 5 page frames, there

is a hit ratio of 3/15. This computation is left as an exercise.

Another replacement algorithm of theoretical interest is the optimal replacement policy. When there is a need to replace a page, choose that page which may not be needed again for the longest period of time in the future.

The following numerical example explains this concept.

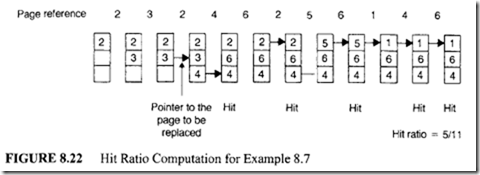
Example 8.7

Using the optimal replacement policy, calculate the hit ratio for the stream of page references specified in Example 8.6. Assume the main memory has three frames and initially all of them are vacant.

Solution

The hit ratio computation for this problem is shown in Figure 8.22.

From Figure 8.22, it can be seen that the first two page references generate page faults. There is a hit with the sixth page reference, because the required page (page 2) is found in the main memory. Consider the fifth page reference. In this case, page 6 is required. Since this page is not in the main memory, it is fetched from the secondary memory. Now, there are no vacant page frames. This means that one of the current pages in the main memory has to be selected for replacement. Choose page 3 for replacement because this page is not used for the longest period of time. Page 6 is loaded into this position. Following the same procedure, other entries of this figure can be determined. Since 6 out of 11 page references generate a page fault, the hit ratio is 5/11.

The decision made by the optimal replacement policy is optimal because it makes a decision based on the future evolution. It has been proven that this technique does not give any anomalous results when the number of page frames is increased. However, it is not possible to implement this technique because it is impossible to predict the page references well ahead of time. Despite this disadvantage, this procedure is used as a standard to determine the efficiency of a new replacement algorithm. Since the optimal replacement policy is practically unfeasible, some method that approximates the behavior of this policy is desirable. One such approximation is the least recently used (LRU) policy.

According to the LRU policy, the page that is selected for replacement is that page that has not been referenced for the longest period of time. Example 8.8 illustrates this.

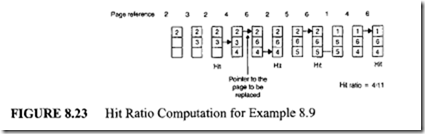
Example 8.8

Solve Example 8.7 using the LRU policy.

Solution

The hit ratio computation for this problem is shown in Figure 8.23.

In the figure we again notice that the first two references generate a page fault,

whereas the third reference is a hit because the required page is already in the main memory. Now, consider what happens when the fifth reference is made. This reference requires page 6, which is not in the memory.

Also, we need to replace one of the current pages in the main memory because

all frames are filled. According to the LRU policy, among pages 2, 3, and 4, page 3 is the page that is least recently referenced. Thus we replace this page with page 6. Following the same reasoning the other entries of Figure 8.23 can be determined. Note that 7 out of 11 references generate a page fault; therefore, the hit ratio is 4111. From the results of the example, we observe that the performance of the LRU policy is very close to that of the optimal replacement policy. Also, the LRU obtains a better result than the FIFO because it tries to retain the pages that are used recently.

Now, let us summarize some important features of the LRU algorithm.

• In principle, the LRU algorithm is similar to the optimal replacement policy except that it looks backward on the time axis. Note that the optimal replacement policy works forward on the time axis.
• If the request stream is first reversed and then the LRU policy is applied to it, the result obtained is equivalent to the one that is obtained by the direct application of the optimal replacement policy to the original request stream.
• It has been proven that the LRU algorithm does not exhibit Belady’s anamoly. This is because the LRU algorithm is a stack algorithm. A page-replacement algorithm is said to be a stack algorithm if the following condition holds:

P₁,(i) C P₁(i + 1)

In the preceding relation the quantity Pt(i) refers to the set of pages in the main memory whose total capacity is i frames at some time t. This relation is called the inclusion property. One can easily demonstrate that FIFO replacement policy is not a stack algorithm. This task is left as an exercise.

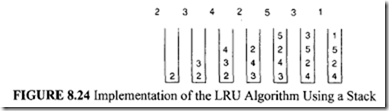
• The LRU policy can be easily implemented using a stack. Typically, the page numbers of the request stream are stored in this stack. Suppose that p is the page number being referenced. If p is not in the stack, then p is pushed into the stack. However, if p is in the stack, p is removed from the stack and placed on the top of the stack. The top of the stack always holds the most recently referenced page number, and the bottom of the stack always holds the least-recent page number. To see this clearly, consider Figure 8.24, in which a stream of page references and the corresponding stack instants are shown. The principal advantage of this approach is that there is no need to search for the page to be replaced because it is always the bottom most element of the stack. This approach can be implemented using either software or microcodes. However, this method takes more time when a page number is moved from the middle of the stack.
• Alternatively, the LRU policy can be implemented by adding an age register to each entry of the page table and a virtual clock to the CPU. The virtual clock is organized so that it is incremented after each memory reference. When a page is referenced, its

age register is loaded with the contents of the virtual clock. The age register of a page holds the time at which that page was most recently referenced. The least-recent page is that page whose age register value is minimum. This approach requires an operating system to perform time-consuming housekeeping operations. Thus the performance of the system may be degraded.

• To implement these methods, the computer system must provide adequate hardware support. Incrementing the virtual clock using software takes more time. Thus the operating speed of the entire system is reduced. The LRU policy can not be implemented in systems that do not provide enough hardware support. To get around this problem, some replacement policy is employed that will approximate the LRU policy.
• The LRU policy can be approximated by adding an extra bit called an activity bit to each entry of the page table. Initially all activity bits are cleared to 0. When a page is referenced, its activity bit is set to I. Thus this bit tells whether or not the page is used. Any page whose activity bit is 0 may be a candidate for replacement. However, the activity bit cannot determine how many times a page has been referenced.
• More information can be obtained by adding a register to each page table entry. To illustrate this concept, assume a 16-bit register has been added to each entry of the page table. Assume that the operating system is allowed to shift the contents of all the registers l bit to the right at regular intervals. With one right shift, the most-significant bit position becomes vacant. If it is assumed that the activity bit is used to fill this vacant position, some meaningful conclusions can be derived. For example, if the content of a page register is 0000 16,then it can be concluded that this page was not in use during the last 16 time-interval periods. Similarly, a value FFFF 16 for page register indicates that the page should have been referenced at least once in the last 16 time­ interval periods. If the content of a page register is FF00 16 and the content of another one is OOF0 16, the former was used more recently.
• If the content of a page register is interpreted as an integer number, then the least-recent page has a minimum page register value and can be replaced. If two page registers hold the minimum value, then either of the pages can be evicted, or one of them can be chosen on a FIFO basis.
• The larger the size of the page register, the more time is spent by the operating system in the update operations. When the size of the page register is 0, the history of the system can only be obtained via the activity bits. If the proposed replacement procedure is applied on the activity bits alone, the result is known as the second­ chance replacement policy.
• Another bit called a dirty bit may be appended to each entry of the page table. This bit is initially cleared to 0 and set to 1 when a page is modified. This bit can be used in two different ways:
• The idea of a dirty bit reduces the swapping overhead because when the dirty bit of a page to be replaced is zero, there is no need to copy this page into the secondary memory, and it can be overwritten by an incoming page. A dirty bit can be used in conjunction with any replacement algorithm.
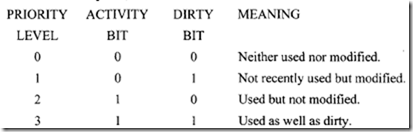
• A priority scheme can be set up for replacement using the values of the dirty and activity bits, as described next.

Using the priority levels just described, the following replacement policy can be formulated: When it is necessary to replace a page, choose that page whose priority level is minimum. In the event of a tie, select the victim on a FIFO basis.

In some systems, the LRU policy is approximated using the least frequently used (LFU) and most frequently used (MFU) algorithms. A thorough discussion of these procedures is beyond the scope of this book.

• One of the major goals in a replacement policy is to minimize the page-fault rate. A program is said to be in a thrashing state if it generates excessive numbers of page faults. Replacement policy may not have a complete control on thrashing. For example, suppose a program generates the following stream of page references:

1,2,3,4, 1,2,3,4, 1,2,3,4, …

If it runs on a system with three frames it will definitely enter into thrashing state even if the optimal replacement policy is implemented.

• There is a close relationship between the degree of multiprogramming and thrashing. In general, the degree of multiprogramming is increased to improve the CPU use. However, in this case more thrashing occurs. Therefore, to reduce thrashing, the degree of multiprogramming is reduced. Now the CPU utilization drops. CPU utilization and thrashing are conflicting performance issues.