Third Law, Carnot Cycle, & Absolute Entropy
Entropy & Reversible Change
The Second Law tells us what happens to Stot under a spontaneous irre- versible change. What happens to Stot under a reversible change? Recall that all thermodynamic changes are “reversible” for the surroundings; therefore, a reversible change for the system must also be reversible for the total system.
Consequently, under a reversible change:
Thus, the information about the total system is conserved under a reversible change; whatever information is gained about the system is lost about the surroundings, or vice-versa. This situation is reminiscent of the balance between volume and temperature information that characterizes the system under reversible adiabatic expansions, resulting in ΔS = 0. We now see that reversible adiabatic changes also satisfy ΔSsur = ΔStot = 0.
Expansions of this kind form a key part of the Carnot cycle (Section 13.2), and will therefore be reviewed here.
Reversible adiabatic expansion of ideal gas: Recall from Sections 8.5 and 9.1 that a reversible isothermal expansion can be achieved by placing a piston-cylinder apparatus in a heat bath, and then slowly easing up on Psur. The resultant reversible path is an isotherm, given for the ideal gas by P(V ) ∝ V −1.
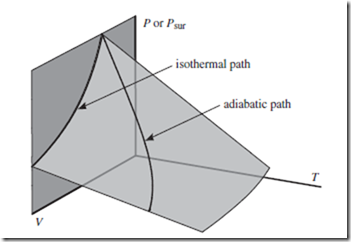
To achieve reversible adiabatic expansion, we surround the apparatus in some thermally insulating material, rather than a heat bath—but otherwise we proceed similarly. Because work is done but no heat is absorbed, U and T both decrease. The resultant reversible adiabatic path, or “adiabat,” is thus different from the corresponding isotherm—although both paths lie on the equation of state, as indicated in Figure 13.1.
For the ideal gas, the projection of the reversible adiabatic path onto (P, V ) space yields P(V ) ∝ V −, where is the adiabat coefficient (p. 70).
Recall that is a constant, with a value greater than one (because CP > CV ). Consequently, the adiabat represents a power law—like the corresponding isotherm, but with a larger inverse power, resulting in a steeper decline. This
Figure 13.1 Reversible and isothermal paths. All reversible paths must lie on the equation of state—represented here as the translucent curved surface. All isothermal paths, including irreversible ones, must lie within a surface of constant T —such as the dark gray vertical plane indicated (and used also in Fig. 8.2). The intersection of these two surfaces defines the reversible isothermal path—but there are many other reversible paths along which T changes, such as the adiabatic path indicated.
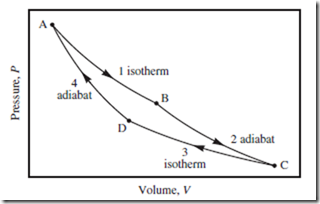
Figure 13.2 Four stages of the Carnot cycle. The four stages of the Carnot cycle, in terms of the piston-cylinder apparatus of Fig. 8.1. Stage 1: isothermal; insert apparatus in high T = Th bath, slowly expand. Stage 2: adiabatic; remove apparatus from bath, insulate, slowly expand. Stage 3: isothermal; insert apparatus in low T = Tc bath, slowly compress. Stage 4: adiabatic; remove apparatus from bath,insulate, slowly compress.
behavior also reflects the fact that during a reversible adiabatic expansion, T decreases along with P (see Figure 13.1 and also Figure 13.2).
Carnot Cycle & Absolute Zero Temperature
The Carnot cycle is the quintessential thermodynamic cycle, covered in every thermodynamics textbook. It provides a useful and quantitative understanding of the operation of heat engines (Section 12.1), whereas the reverse Carnot cycle does the same for heat pumps (e.g., air conditioners). It is also an excellent example for analyzing how entropy behaves under reversible change—in which context, it relates to the Third Law of Thermodynamics.
In a Carnot cycle, the “loop” is a precise set of four consecutive but reversible stages, as indicated in Figure 13.2. Two of these stages are expansions, and two are compressions. Also, two are isothermal, and two are adiabatic. Being a cycle, for all state functions X , ΔX is zero around the entire cycle—but not necessarily zero over each individual stage. Finally, W = −Q ≠ 0 around the entire cycle—with (W < 0, Q > 0) corresponding to a clockwise traversal (heat engine), and (W > 0, Q < 0) to the reverse or counterclockwise traversal (heat pump).
In practice, care must be taken to ensure that every stage is as reversible as possible. For example, heat flow must be avoided when the apparatus is inserted into the hot bath at state A (or cold bath at state C), by ensuring that T is equal to Th (or Tc), at the end of the preceding adiabatic stage 4 (or 2).
which says that the wasted heat can be minimized by maximizing the temperature ratio between hot and cold heat baths. Conversely, the efficiency of the heat engine—or ratio of work performed to absorbed heat—is defined as = | | Qh = (1 − Tc∕Th). Both this expression and Equation (13.1) are completely general—i.e., applicable to both ideal gases and other materials.
Remarkably, depends only on the temperature ratio, and not at all on the properties of the heat engine itself! The other side of this coin, though, is that for fixed Tc and Th, is always less than one, and cannot be increased.
Only in the limit that Tc → 0 does → 1. Note also that Tc < 0 would result in > 1—an obviously physically incorrect prediction that reconfirms the absolute zero limit on temperature.
Real heat engines are even less efficient than predicted above. In part, this is due to some inevitable irreversibility, which always reduces (see Sections 14.3 and 14.4). In part, though, also, this is by design; power stations, for example, are usually optimized for power (rate of work), rather than efficiency.
Third Law & Absolute Entropy
The final Law of Thermodynamics is the Third Law, which—like the Second Law—also deals with entropy. Our introduction to the Third Law will be empirical—like that of the Second Law in Section 12.1.
Consider a material that can transform between two different condensed phases. The entropy change associated with this (reversible) phase transition is denoted ‘ΔtrsS’. It is an experimental fact that in all such cases, ΔtrsS → 0 as T → 0. Thus, both phases approach the same S value. If we take the S(T = 0) value to be zero, we obtain the Third Law: The absolute entropy of the system approaches zero as the abso- lute temperature approaches zero:
S → 0 as T → 0 [always] (13.2)
Are we allowed, though, to simply “set” S = 0? We are, if we use the thermodynamic definition of Equation (10.1)—according to which, S is defined only up to an additive constant. In this context, the Third Law thus converts relative to absolute entropies—essentially serving to define the additive constant for the latter.
Using the information Definition 10.3, however, absolute entropies are obtained directly (in principle at least)—and so the Third Law must be proved, not just assumed. The Boltzmann distribution of Equation (6.1) implies that as T → 0, the system spends all of its time in just a single molecular state. Thus, Ω → 1 as T → 0, and so according to Equation (10.2), S → 0.
⊳⊳⊳ To Ponder… The ΔS form of the Third Law is called the Nernst theorem; the S form is due to Planck. It could be argued that the former is the actual physical law, since S cannot be measured directly.
⊳⊳⊳ Don’t Try It !! Don’t try to apply the Third Law to the Sackur-Tetrode expression [Equation (11.11)]—which predicts negative infinite S as T → 0. This fails because the ideal gas law is invalid in the T → 0 limit.