Second Law & Spontaneous Irreversible Change
Heat Engines & Thermodynamic Cycles
Perhaps the best way to introduce the Second Law of Thermodynamics is still the original way—i.e., in the context of heat engines. Conceptually, the notion of a thermodynamic heat engine is straightforward: it is a device that absorbs heat energy, (some of) which it then converts into work done on its surroundings.
Implicit in the use of the word “engine” is the idea that the device can be used repeatedly over time. Thus, whereas some kind of thermodynamic change is obviously required in order to generate nonzero W , we can- not rely on changes that perpetually increase V . Instead, heat engines use cycles—loop paths in state space that return to where they started, thereby incorporating both expansion and compression stages.
Similar considerations must also hold for temperature; any T increase must be balanced by an equal and opposite T decrease, somewhere else within the cycle. A naive individual might imagine that Q must also be balanced around such a cycle—whatever heat is absorbed must later be released. This is false; Q ≠ 0 around a cycle, precisely because Q is not a state function.
The work must also be nonzero around a cycle—otherwise, heat engines would not function! Therefore—and although it can make solving thermodynamics problems a pain—the path-function aspect of Q and W is actually critically important. Note finally that the cycle must loop around clockwise in (P, V ) space, in order for W < 0. Thus, the expansion stage(s) occurs at higher P (and higher T) than the compression stage(s). We will examine heat engines more quantitatively in Section 13.2, in the context of the Carnot cycle; here, the discussion remains more conceptual.
Traditional Statements of the Second Law
The “naive observer” from Section 12.1 has now learned, presumably to his or her amazement, that heat engines do exist. Around a cycle, the total Q—i.e., the difference between absorbed and released heat—is not zero, but is in fact equal to the total work done, −W . Note that the bigger the heat difference, the greater the work performed—motivating the design of heat engines for which released heat is as small as possible.
Is it possible to build a “perfect” heat engine—i.e., one for which there is no released heat, so that all absorbed heat is converted into useful work? Let’s suppose that our naive observer now imagines this new scenario to be the case—i.e., the exact opposite of his or her earlier stance. He or she would, once again, be wrong. The reason turns out to be the Second Law. Most engineering and many science textbooks introduce the Second Law through a standard series of Statements—more or less identical to the conclusion of the previous paragraph, and to each other. More precisely: the basic description above is the Kelvin Statement; the (necessary!) restriction to cycles (introduced by Max Planck) gives rise to the Kelvin-Planck Statement; the converse statement (i.e. running the cycle in reverse) is the Clausius Statement.
Textbooks that present the formal Statements above may do so for sev- eral reasons—e.g., because of historical tradition, and/or because heat engines are still very relevant today. Another likely reason, though, is because they typically introduce the Second Law before introducing entropy. Even those science texts that do not list the formal Statements almost invariably provide an “arrow” diagram, showing heat flow in being split into work flow out plus heat flow out. Such a diagram constitutes a pictorial representation of the same basic principle.
⊳⊳⊳ To Ponder… The idea of heat flowing into the engine, rather than out of it, may seem strange to modern- day automobile drivers—but not to their turn-of-the-last- century counterparts! (There were, indeed, steam-powered automobiles … See Appendix C.) This is, in fact, one of the primary differences between the steam engine and the internal combustion engine.
The Second Law Statements above preclude the existence of what is called a perpetual motion machine of the second kind. Proposals for machines of this kind have enjoyed a rich and colorful history—leading to innumerable patent applications, and even out and out fraud. All such devices are impossible, however—due to the fact that the Second Law is, in fact, a law (Section 2.2). Indeed, as useful as the heat engine application turns out to be, it is merely one example of a much broader and more important general principle—the Second Law—whose real significance depends fundamentally on the concept of entropy.
⊳⊳⊳ To Ponder… Rudolf Clausius (see Appendix A), of the above Clausius Statement, discovered the entropy interpretation of the Second Law, and also coined the term “entropy” from a Greek word meaning “transformation.” In doing so, he very fortunately abandoned his earlier term for this fundamental quantity—which was “verwandlungsinhalt”!
Entropy Statement of the Second Law
In the same manner that energy plays a fundamental role vis-a`-vis the First Law, entropy plays a fundamental role in the Second Law, given here:
Second Law (total system): The entropy of the total system increases under any spontaneous irreversible thermodynamic change:
We emphasize from the start that in its most fundamental form above, the Second Law of Thermodynamics is a statement about the total system. In that respect, Equation (12.1) very much resembles the most fundamental form of the First Law—i.e., Equation (7.2).
One critical difference from Equation (7.2), however, is that Equation (12.1) is an inequality, rather than an equality (conservation law). Much can and has been made of this inequality feature of the Second Law. Some authors—e.g., Raff—put a negative spin on this:
[The Second Law]…is the only scientific law that is stated in negative terms. It tells us what we cannot do.
Some people may like to believe that the “sky is the limit”—that we can achieve anything at all, if we are merely ingenious enough. But generally speaking, this expectation is unrealistic and naive. There are always limits, and it is in fact a very good thing to know those limits in advance. In any case, there are a few other “inequality limit” laws in science, such as the speed-of-light limit on the speed of moving particles (special relativity) and also the absolute zero limit on temperature (intimately connected with the Third Law, Section 13.3).
In any case, the most important ramification of the Second Law inequality is that spontaneous irreversible change occurs in one direction only. Consider running any spontaneous irreversible process in reverse; ΔStot is now negative, and thus forbidden by the Second Law. Such “nonspontaneous” irreversible processes, though hypothetically possible, do not actually occur in nature. Many examples from everyday experience may be considered— a glass knocked off a counter falls on the ground and shatters into many pieces, but the reverse process is never seen.
The above, “arrow of time” feature of the Second Law is all the more profound, given that the underlying molecular laws of physics themselves do not appear to have any time directionality built into them. It is an inherently “emergent” property (Section 2.1) that continues to occupy the great scientific minds of the present day, such as Stephen Hawking.
Entropy and the Second Law are often interpreted in energetic terms. More precisely, entropy relates to the distribution or dispersal of energy— with the Second Law implying that over time, energy becomes more uniformly distributed throughout the total system. According to the Second Law, everything in the universe will eventually reach thermal equilibrium— making the operation of heat engines impossible, for instance. Whether this depressing “heat death” will ever actually be realized is still an open question—though it has preoccupied people since the late 19th century (see Appendix B). In any event, energy dispersal, etc., ultimately pertains to the available molecular states—thus leading us to consider the information the- ory viewpoint.
Information Statement of the Second Law
Definition 10.1 (p. 79) has quite interesting ramifications for the Second Law of Thermodynamics, which can be interpreted in information terms as follows:
Second Law (information): Information about the total system decreases under a spontaneous irreversible change.
In the Statement above, and henceforth, the word “information” is used as a shorthand for:
. amount of molecular information known by a macroscopic observer
Since the Second Law implies an increase in the total system entropy as an inevitable consequence of each spontaneous irreversible change that takes place, our ignorance about the universe increases—and therefore our information decreases—as time progresses. This rather depressing conclusion may seem counterintuitive.Keep in mind, however, that “information” in this context has a very limited and literal meaning, in terms of the positions, velocities, etc. of molecules.
Put another way, the number of molecular states available to the total system increases over time, during the course of a spontaneous irreversible change. Why should this be the case? This is because of the causative sudden external change—which always serves to remove some previous macroscopic restriction on the total system (a tire is suddenly punctured; a fixed wall is suddenly released; heat is suddenly allowed to flow, etc.). Removing macroscopic restrictions increases the number of available molecular states—thereby placing the total system in a “less special” final thermodynamic state.
Ultimately, the Second Law holds because the universe itself started out in a very special thermodynamic state—for which there were many restrictions, few corresponding molecular states, and a very low Stot. By its demise, the universe may well see all of its macroscopic restrictions removed, and all of its parts in perfect equilibrium with each other—the aforementioned “heat death.”
Recalling the “arrow of time” discussion in Section 12.3, it is worth considering how the Second Law “emerges” in the large N limit—e.g., in the context of the punctured tire system example (box on p. 27). Consider monitoring a single air molecule, starting from the instant that the tire is punctured (t = 0). Within a certain time interval, we might well observe this molecule moving from the outside to the inside of the tire, and think nothing of it; this event may be only slightly less probable than its opposite (i.e., moving from inside to outside), and in any case, the molecular laws of physics are time-reversible.
On the other hand, if we were to observe all of the N ≈ NA particles of the macroscopic (total) system, moving from outside to inside the tire, during the same time interval, this would be an extremely improbable— even unnatural—event. Such a scenario accurately describes what would have to happen if the punctured tire “movie” were run in reverse.
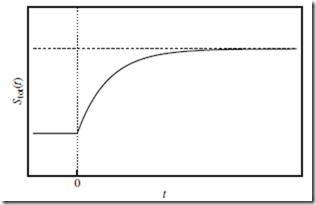
Some authors prefer to speak of “natural” and “unnatural” processes, rather than “spontaneous” and “nonspontaneous” processes—and perhaps wisely so. Such nomenclature correctly suggests, e.g., that the spontaneous accumulation of air molecules inside the punctured tire— and the commensurate reduction in the number of available molecular states and Stot—is in fact statistically possible. However, the likelihood of such a process actually occurring in nature becomes overwhelm- ingly improbable when N is large. Almost always, Stot(t) increases with t during the course of a spontaneous irreversible change, as indicated in Figure 12.1.
Figure 12.1 Entropy of the total system as a function of time. Entropy of the total system, Stot (solid curve), as a function of time, t, during the course of a spontaneous irreversible change—in response to a sudden external change applied at t = 0 (vertical dotted line). Initially, Stot(t) increases with t, as the total system explores more of the molecular states now available to it. Eventually, Stot(t) approaches a new constant (horizontal dashed line), indicating that a new equilibrium has been reached.
⊳⊳⊳ To Ponder…at a deeper level. Since entropy is a state function, and the thermodynamic state may not even be well defined during the course of an irreversible thermodynamic change (Section 8.4), how can we determine Stot(t) in Figure 12.1? This can be done by monitoring the particle probability distributions (Section 6.1) over time. When the sys- tem is out of equilibrium, the position distribution is not uniform, and the velocity distribution is not the Maxwell-Boltzmann distribution. Only for t < 0 and t → ∞—i.e., the initial and final (equilibrium) states, respectively—do the distributions take these standard forms.
⊳⊳⊳ To Ponder…at a deeper level. Though extremely rare when N is large, statistical fluctuations that appreciably reduce the value of Stot do occur—it is merely a matter of waiting long enough. Boltzmann himself considered the role that such fluctuations might play in a “heat death” end-of-the-universe scenario. Recently, this question has once again become a hot topic in the field of cosmology, where fluctuations are (seriously) imagined to give birth to whole new universes. (No one can accuse cosmologists of not taking ideas to their absolute extreme limits—it is their raison d’eˆtre, after all…) On the other hand, rather than creating a whole new universe comprised of a multitude of stars, galaxies, intelligent observers, etc., would it not be far easier simply to create a single brain that merely (and erroneously) believes in all of this rich external structure? Both scenarios are consistent with experience—yet the latter, as improbable as it sounds, is presumably far more likely. This is the Boltzmann brain paradox.
Maximum Entropy & the Clausius Inequality
Figure 12.1 implies that after a sudden external change, equilibrium is restored again only after Stot reaches a maximum value. This is known as the principle of maximum entropy, and it is very useful for predicting the final equilibrium state that ensues after a spontaneous irreversible change has occurred.
Thus, the maximum entropy state for the above example is also the mechanical equilibrium state, as per Section 4.3. Similar arguments for two subsystems in thermal contact can be used to show that—in that case— heat flows until S is maximized, which occurs when TA,f = TB,f (i.e., the condition for thermal equilibrium).
In the box above, we used the subsystems picture of Section 4.3. Going forward, however, the total system or “system-plus-surroundings” picture will be more appropriate, because we will be deriving a new form of the Second Law that applies directly to the system itself.
⊳⊳⊳Don’t Try It !! Don’t assume that ΔS > 0 for a spontaneous irreversible change! ΔS can also be negative—for the same reason that ΔU can be nonzero—because the First Law [Equation (7.2)] and the Second Law [Equation (12.1)] apply to the total system, not to the system itself.
Thus, whereas it is possible to restore the system to its original state, after it has first undergone an irreversible change, it is never possible to restore the total system to its original state, after an irreversible change. To do so would violate the Second Law.
Building on the discussion in Section 7.1, a key difference between the system and surroundings is that the latter are regarded to be in equilibrium with themselves throughout an irreversible change. Thus, quantities like Psur and Ssur are always well defined.
⊳⊳⊳ To Ponder… Right around this point in many of the reference textbooks, you will notice that the ‘ex’ or similar subscript used to denote the surroundings, suddenly changes to something like ‘sur’. Could this be to avoid the awkwardness of ‘Sex’? The serious point here: there is essentially no difference between the “externals” and the surroundings.
Consider the derivation provided in the box below. This gives rise to the Clausius inequality, a form of the Second Law that applies directly to the system:
Second Law (differential form): Under any spontaneous irreversible infinitesimal thermodynamic change,
Equation (12.2) above is thus analogous to the differential form of the First Law [Equation (8.1)]. Note that dS can indeed be negative—but only if dQ is also negative.