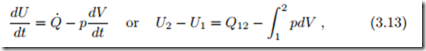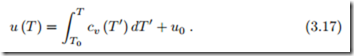The First Law for Reversible Processes
The form (3.1) of the first law is valid for all closed systems. When only reversible processes occur within the system, so that the system is in equilibrium states at any time, the equation can be simplified as follows: From our discussion of equilibrium states we know that for reversible processes the system will be homogeneous, and that all changes must be very slow, which implies very small velocities. Therefore, kinetic energy can be ignored, Ekin = 0. Stirring, which transfers energy by moving the fluid and friction, is irreversible, hence in a reversible process only moving boundary work can be transferred. As long as the system location does not change, the potential energy does not change, and we can set Epot = 0.
With all this, for reversible (quasi-static) processes the first law of thermodynamics reduces to
where the second form results from integration over the process duration. We shall later, in particular in Chapter 7, use this equation extensively to study reversible processes in closed systems.
The Specific Heat at Constant Volume
We consider a closed system heated at constant volume (isochoric process), where the first law (3.13) reduces to (recall that U = mu (T, v) and m = const.)
From this equation we see that cv is the amount of heat required to increase the temperature of 1 kg of substance by 1 K at constant volume. The specific heat can be measured by controlled heating of a fixed amount of substance in a fixed volume system, and measurement of the ensuing temperature difference; its SI unit is ![]()
In general is a function of temperature and specific volume. For incompressible liquids and solids the specific volume is constant, v = const, and the specific heat is a function of temperature alone. Interestingly, also for ideal gases the specific heat turns out to be a function of temperature alone, both experimentally and from theoretical considerations.
For these materials the internal energy depends only on temperature, and integration gives the caloric equation of state as
Only energy differences can be measured, where the first law is used to evaluate careful experiments. The choice of the energy constant u0 = u (T0) fixes the energy scale. The actual value of this constant will only become relevant for the discussion of chemical reactions. Note that proper mathematical notation requires to distinguish between the actual temperature T of the system, and the integration variable T I.
For materials in which the specific heat varies only slightly with temperature in the interval of interest, the specific heat can be approximated by a suitable constant average cavg , so that the caloric equation of state assumes the particularly simple linear form
Enthalpy
In many thermodynamic calculations one encounters the combination U +pV , or the mass divided equivalent u+pv, and it is convenient to introduce a name and a symbol for these. We define the total and the specific enthalpy as
While its internal energy depends only on temperature, the enthalpy of an incompressible substance (constant specific volume v) depends on temperature and pressure. Indeed, by its definition h = u + pv, enthalpy depends explicitly on pressure. With h0 as the enthalpy at a reference point (T0, p0), the enthalpy for an incompressible solid or liquid with constant specific heat becomes
Note that no substance is truly incompressible, normally the specific volume changes at least a little bit. This leads to small differences between specific heats which can be ignored as long as the compressibility is sufficiently small.
Related posts:
Incoming search terms:
- first law of thermodynamics is valid for
- frist law of thermodaynamic why only valid for reversible process
- form of first law of thermo valid only for reversible syestem
- First law of thermodynamics is valid for which processes
- 1st law of thermodynamics valid fow which process
- first law of thermodynamics eqfuation for reversible process
- first law of thermodynamic is valid for
- first law in reversible process
- constant volume specific heat equation
- is first law valid for all processes