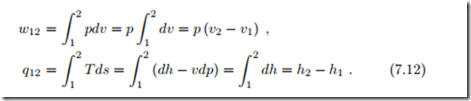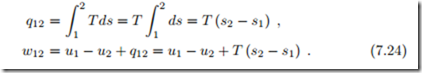Reversible Processes in Closed Systems:Isochoric Process: v = const., dv = 0 and Isobaric Process: p = const., dp = 0.

Isochoric Process: v = const., dv = 0

Isochoric processes (constant volume) can be easily realized by ﬁxing the volume, e.g., by clamping the piston, see Figure 7.3 for process sketch and diagrams.

With dv = 0 in the constant volume process, heat and work follow from (7.7, 7.8) as

We compute the process curve of an isochoric process in the T-s-diagram for an ideal gas with constant speciﬁc heats. From the Gibbs equation and the caloric equation of state we ﬁnd for the isochoric process

Thus, for an ideal gas, the isochoric process in the T-s-diagram follows an exponential, as indicated in the T-s-diagram.

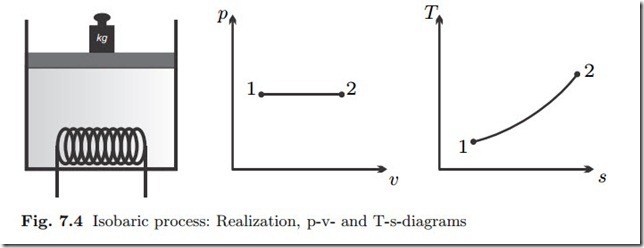
Isobaric Process: p = const., dp = 0

Isobaric processes (constant pressure) are easily realized by free pistons, where the piston weight controls the pressure; see Fig. 7.4 for process sketch and diagrams.

With dp = 0 in the constant pressure process, heat and work follow from (7.7, 7.8) as

Here we have used the Gibbs equation in the form (4.13), T ds = dh − vdp.

Again we compute the process curve in the T-s-diagram for an ideal gas with constant speciﬁc heats. From the Gibbs equation and the caloric equation of state we ﬁnd for the isobaric process

This was used for drawing the curve in the diagram. For an ideal gas, the isobaric process in the T-s-diagram follows an exponential. Since cp = cv + R > cv , isobaric lines in the T-s-diagram are not as steep as isochoric lines starting at the same point.

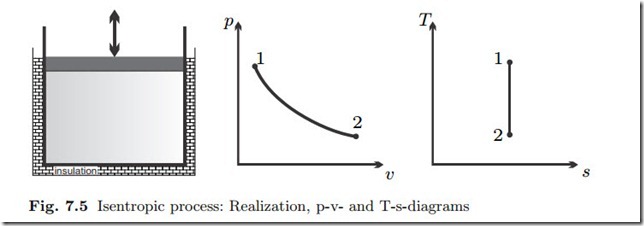
Isentropic Process: q12 = δq = ds = 0

A system that is insulated against heat transfer is adiabatic. However, adiabatic processes are also realized if the process is suﬃciently fast, so that there is no time to exchange heat. A pressure disturbance at the boundary, i.e., induced by the moving piston, travels with the speed of sound, and ac- cordingly mechanical equilibrium in the working ﬂuid is assumed rather fast. A temperature disturbance at the boundary, however, diﬀuses slowly into the working ﬂuid. In other words, pressure equilibration and heat transfer occur on quite distinct time scales. Accordingly, a compression (i.e., pressure in- crease) or expansion (i.e., pressure decrease) process may be slow enough to allow for pressure equilibration in the system, but at the same time may be so fast that there is no time to exchange heat between the working ﬂuid and the system walls, even if they have diﬀerent temperatures. Such a process can be modelled to be (approximately) adiabatic.

From the relation between entropy and heat for reversible processes (7.6) follows for an adiabatic process

The value of the ratio of speciﬁc heats is k = 1.667 for monatomic gases, and, under the cold-gas approximation, k = 1.4 for diatomic gases, and k = 1.333 for polyatomic gases. Equations (7.23) are the adiabatic relations for ideal gases with constant speciﬁc heats.

Isothermal Process: T = const, dT = 0

Isothermal processes require exchange of heat with a large reservoir at constant temperature. Since heat exchange is slow, isothermal processes must be rather slow and therefore they are not found in the most common thermo- dynamic cycles. Figure 7.6 shows process sketch and diagrams.

Since temperature is constant, heat and work can be computed as

We consider the special case of the ideal gas where p = RT , which was used to draw the curve in the p-v-diagram. With the thermal equation of state explicitly known, the work can also be determined by integration (recall T is constant!),