Entropy of a Gas Mixture
Entropy of a gas mixture Sm = Sa + Sb + Sc + …….
The specific entropy on the mass basis
n differentiating we get
(dS)m = mfa (ds)a + mfb (ds)b + mfc (ds)c + ……
Expressing the entropy of a perfect gas as a function of temperature and pressure, the change in entropy is given by
On substituting this expression in the above equation, the change in entropy of a gas mixture in the differential form becomes
Assuming the specific heats as constant and integrating the above equation between states (1) and (2), the change in entropy of the perfect gas mixture on the mass basis can be written as
where pa, 1, pb, 1 pc, 1 etc are partial pressures at state one and pa, 2, pb, 2 pc, 2 etc are partial pressures at state 2 of the constituent gases, a, b, c, etc respectively.
Isentropic process of gaseous mixture:
When the mixture of gases is compressed or expanded from state (1) to state (2) isentropically,
Adiabatic Mixing of Perfect Gases Initially at Same Temperature and Pressure Consider several gases of mass ma, mb, mc etc at the same temperature T and pressure p confined in separate compartment of an adiabatic vessel. When the partitions between compartments are pulled out from the vessel, the gases mix with each other until a new
equilibrium state is attained.
Since in an adiabatic mixing processes, there is no heat transfer and also no work crosses the boundary of the system, for a closed system DU = 0 i.e., Uinitial = Ufinal. Hence the resulting temperature of the mixture remains the same as that of each gas before mixing. In other words, the mixing process is isothermal. However each gas after free expansion will attain the partial pressure of the mixture and each gas will occupy the entire volume of the vessel. By using the perfect gas equation, it can be shown that the total pressure of the mixture is equal to the initial pressure p of each individual gas.
As the mixing process is irreversible, according to the second law of thermodynamics, the entropy of the mixture increases. Assuming constant specific heats, the change in entropy of the gas a is given by
Where the subscripts (1) and (2) refer to the initial and final states of the component a in the mixture.
Since the partial pressure pa,2 is less than the partial pressure pa,1 of the mixture which is equal to p, the pressure of the individual gas, the change in entropy is always positive. This conclusion is consistent with the fact that for an irreversible process, entropy always increases.
Similarly the change in entropy of the gas b
Hence the total change in entropy of the mixture is
It is evident from the above equation that the increase in entropy of the mixture of perfect gases depends only on the number of moles of the component gases and is independent of the nature of the individual gases.
Adiabatic Mixing of Perfect Gases Initial at Different Pressure and Temperature:
Consider several gases of mass ma, mb, mc, etc, initially at different pressure and temperature confined at separate compartments in a thermally insulated vessel (adiabatic vessel). When the partitions are removed, the gases mix with one another. The mass and volume of the mixture are given by
Where, ma, mb, mc, …. are the initial masses and Va, Vb, Vc …. are the initial volumes of each constituent respectively.
Since during the mixing process there is no heat and work interaction, the change in internal energy of the system is zero, i.e., the sum of the internal energies of the individual gases before mixing is equal to the internal energy of the mixture.
Since it is a irreversible adiabatic mixing process, the entropy must increase. Since the change in entropy of the mixture is equal to the sum of the changes in entropies of the individual gases, we can write
The change in entropy of individual gases can be calculated by considering that each individual gas exists alone and is expanded from the initial state to the temperature and volume of the mixture, the pressure at the final state being the partial pressure of the constituent in the mixture. Thus the changes in entropy of the constituent ‘a’ is
Problems
1.The mass analysis of a gas mixture shows that it consists of 60% of N2 & 30% of CO2 & 10% of CO. If the temperature and pressure of the mixture is 200C & 3 bar, compute (i) the partial pressure of the components, (ii) Molecular weight of the mixture, (iii) gas constant for the mixture.
1. b) For a reference state of 00C and 1 bar also determine (i) constant pressure specific heat of the mixture (ii) enthalpy and internal energy of mixture (iii) entropy of mixture.
Solution: Constant pressure molal specific heat of a perfect gas is given by
2. A tank of 0.7 m3 capacity contains O2 at a pressure of 5 bar and 320 K temperature. N2 is introduced without change in temperature until the pressure in the tank becomes 8 bar. Determine the mass of each gas in the tank and partial volume of each gas.
3. a) A gaseous mixture contains 21% by volume of N2, 50% by volume of H2 and 29% by volume of CO2. Calculate the gas constant of the mixture and the ratio of specific heats. If the mixture pressure is at 1 bar and the mixture temperature is 100C, calculate the partial pressures and mass fractions of the constituents.
b) A cylinder contains 0.085m3 of this mixture at 1 bar and 100C. The gas undergoes a polytropic process according to the law Pv1.2 = constant to a final volume which is one fifth of the initial volume. Determine i) the magnitude and direction of work transfer, ii) magnitude and direction of heat transfer and iii) the change in entropy.
Negative sign indicates that work is done by the surroundings on the gas mixture.
Temperature of the mixture at the end of the process is,
4. Calculate the constant volume and constant pressure specific heats of a gas mixture consisting of 1 kg of oxygen and 2 kg of nitrogen at a pressure of 1.5 bar and temperature 200C. Also determine the change in internal energy, enthalpy and entropy of the mixture when it is heated under constant volume to a temperature of 1000C.
5. A gaseous mixture consisting of 1 kg of helium and 2.5 kg of nitrogen is compressed isentropically in a closed system from a pressure of 1 bar, 270C to a pressure of 7 bar. Assuming specific heats of helium and nitrogen to be constant, determine the specific heats of the mixture, the change in entropy of individual gases, and the change in internal energy of the mixture. Also find the work required for the compression process. Assume CvHe = 3.14 kJ/kg-K, CvN2 = 0.741 kJ/kg-K, CpHe = 5.233 kJ/kg-K and CpN2 = 1.038 kJ/kg-K
6. Two thermally insulated vessels, each of 0.85 m3 in volume are isolated from each other by a partition wall. One of the vessels contains nitrogen and the other oxygen, each at 5 bar and 1000C. As soon as the partition between the vessels is removed, the two gases mix adiabatically. Determine the increase in entropy of the gas mixture.
Solution: Since the pressure and temperature of each gas are equal, the pressure and temperature of the mixture will not change, i.e., the mixture will be at 5 bar and 373 K. But the volume of the mixture will be 2×0.85= 1.7m3 and the pressure of N2 and O2 is
7. Two kg-mole of CO2 at a pressure of 1.8 bar, 800C is mixed in a thermally insulated vessel with 3 kg-mole of N2 at 2.2 bar, 600C. When the mixture is at equilibrium, determine the final temperature and pressure and the change in entropy of the mixture. Assume CvCO2 = 0.653 kJ/kg-K, CvN2 = 0.741 kJ/kg-K
Related posts:
Incoming search terms:
- adiabatic mixture of perfect gases
- entropy of gas mixture
- entropy change due to mixing of two different gases
- adiabatic mixing of gas at different temperature
- mixing of two gases in adiabatic vessel
- mixing of gases at different temperatures
- is negetive mixture irreversible
- entropy of a mixture of gases
- entropy change on increasing pressure of n2
- Changes in internal energy (adiabatic process)
- change in entropy formula for nitrogen
- Adiabatic Mixing of Perfect Gases Initially at Same Temperature and Pressure
- adiabatic mixing of perfect gases
- Mixing of two real gases in irreversible process
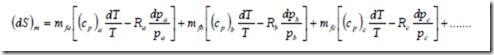

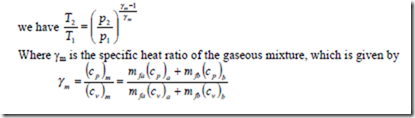
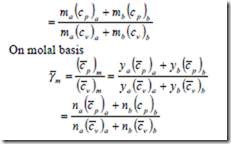
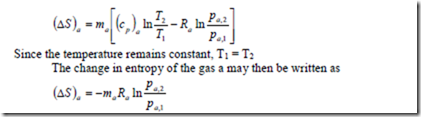
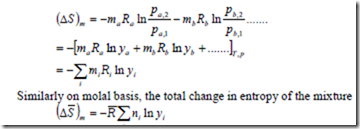





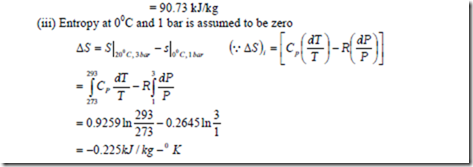

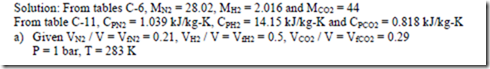

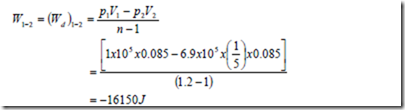

![image_thumb[1] image_thumb[1]](http://lh5.ggpht.com/-wjq6YgOwg1k/VOOA7onL0oI/AAAAAAABQ0E/ts7UOGax4Fg/image_thumb%25255B1%25255D_thumb.png?imgmax=800)
![image_thumb[2] image_thumb[2]](http://lh3.ggpht.com/-urc28eDQww4/VOOA_nGVPBI/AAAAAAABQ0U/Gmcums6H88A/image_thumb%25255B2%25255D_thumb.png?imgmax=800)
![image_thumb[3] image_thumb[3]](http://lh5.ggpht.com/-jbGrMf16bGo/VOOBCjozODI/AAAAAAABQ0k/8kskd5jK_uU/image_thumb%25255B3%25255D_thumb.png?imgmax=800)
![image_thumb[4] image_thumb[4]](http://lh5.ggpht.com/-EAyjJp8IM3s/VOOBGhMztvI/AAAAAAABQ00/AEn3spN2phI/image_thumb%25255B4%25255D_thumb.png?imgmax=800)
![image_thumb[5] image_thumb[5]](http://lh6.ggpht.com/-rC7Wc4Slq4s/VOOBKcjFTMI/AAAAAAABQ1E/_edp8mwxwuI/image_thumb%25255B5%25255D_thumb.png?imgmax=800)
![image_thumb[6] image_thumb[6]](http://lh5.ggpht.com/-pkI-oC9TX6Y/VOOBNaLUzfI/AAAAAAABQ1U/EYT1UVQdK3Y/image_thumb%25255B6%25255D_thumb.png?imgmax=800)
![image_thumb[7] image_thumb[7]](http://lh6.ggpht.com/-h9TmuJL01_4/VOOBR35X-YI/AAAAAAABQ1k/PyaLM3GpH5k/image_thumb%25255B7%25255D_thumb.png?imgmax=800)
![image_thumb[8] image_thumb[8]](http://lh5.ggpht.com/-3m34ayzRbxo/VOOBVuDndBI/AAAAAAABQ10/POEI8D8OtaE/image_thumb%25255B8%25255D_thumb.png?imgmax=800)