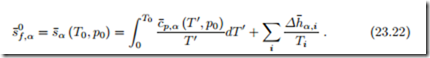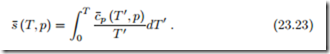The Third Law of Thermodynamics
Also the entropy of a substance can be determined from integration based on measurements of specific heat and the thermal equation of state. Equation (16.35) written for the molar entropy of component α reads
with the entropies of formation s¯0 = s¯α (T0, p0).
The Third Law of Thermodynamics, formulated by Walther Nernst (1864-1941) based on experimental evidence, states that at absolute zero (T = 0 K), the entropy of any crystalline substance is a constant, and independent of pressure and other properties (e.g. magnetization). Based on the microscopic definition of entropy, S = k ln Ω, Max Planck (1858-1947) found that the value of the constant depends on the quantum mechanical ground state, and it is zero for crystals that only have one ground state (Ω = 1); then s (T = 0 K) = 0. Systems with more ground states have a residual entropy.
The third law allows to determine the entropy of formation f,α =s¯α (T0, p0) from (23.21) by evaluating it at T = 0 K and p = p0, which yields 3
For substances with residual entropy, the latter must be added on the right hand side. Thus, the third law assigns absolute values to the entropy constants s¯0 = s¯α (T0, p0), i.e., the entropies of formation, which can be found in tables.
Most data tables for ideal gases show the entropy values s¯α (T, p0) with respect to the proper reference, so that the tabulated value s¯α (T0, p0) is the entropy of formation of α at standard reference conditions. In other words, in contrast to enthalpy data, tabulated entropy data normally needs not to be corrected. A notebale exception are saturation tables, e.g., for water one often finds the reference set such that the entropy of liquid at the triple point is set to zero.
The Third Law and Absolute Zero
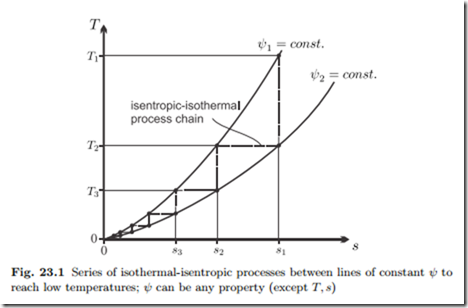
An interesting implication of the third law is that a temperature of absolute zero cannot be reached in a finite number of process steps. This can best be shown with the help of the T-s-diagram in Fig. 23.1, which shows lines of constant property ψ (e.g., pressure, magnetization, . . . ).
Due to the third law, the lines of constant ψ all emerge from one point at T = 0 K. To reach low temperatures, one can take a relatively large amount of substance at (T1, ψ1) and subject it to an adiabatic process ending at (T2, ψ2). Next, one takes a part of the substance at (T2, ψ2) and brings it to (T2, ψ1) isothermally, where the rest of substance at (T2, ψ2) serves as a temperature reservoir. Now one repeats the series of adiabatic and isothermal processes, with smaller and smaller amounts of substance. The resulting zigzag process is shown in the figure, where for simplicity the adiabatic processes are drawn as adiabatic reversible—i.e., isentropic—processes. Since the curves of constant ψ meet in the origin, the distance between the curves becomes smaller and smaller, and each step leads to a temperature reduction smaller than the previous. Accordingly, the heat δq = T ds removed per unit mass in each isothermal step becomes smaller and smaller as well. Evidently, absolute zero cannot be reached with a finite number of steps.
Another conclusion from the third law refers to the specific heat: When phase changes are excluded, specific heat and entropy are related by
Entropy must remain finite in the limit T → 0 K, which implies that the specific heat must vanish in the limit,