Chemical Potential, Fugacity,& Open Systems
What Would Happen If n Were a Variable?
In the early part of this book, the amount of substance, n (or N) was treated as a thermodynamic variable. Since then, we have for simplicity considered only closed systems, for which n is constant. This is fine for describing simple processes such as gas expansions. However, most thermodynamic applications of real-world interest—phase transitions, mixtures, chemical reactions, osmosis, thermoelectric power generation, etc. (see Chapter 17 and the website)—are not so simple. Such processes involve open systems—or those for which n can otherwise change.
How does this affect our thermodynamic picture as developed thus far? Regarding n as a thermodynamic variable, the most basic question is whether or not this variable is independent. Since it is clearly possible to change the thermodynamic state of a system by adding new particles to it—without changing either of the two variables (T, P)—n must indeed be independent.
For an open system consisting of a pure substance in a single phase, there are thus three independent variables in all. In this context, n can only change as a result of diffusion—i.e., the random migration of particles, in or out of the system. The system and surroundings are said to be in diffusive contact, separated by a diffusive or permeable wall.
Though important in its own right, our present study of diffusion is mainly motivated by the desire to set the stage for more complicated processes—specifically, phase transitions, mixtures, and chemical reactions. In such cases, the system is comprised of more than one type of particle— thus requiring multiple independent n variables. Moreover, the particle types can interconvert—allowing for n values to change even if the sys- tem is closed. Though quite involved, a solid understanding of these more advanced topics rests firmly on the foundations laid in this chapter.
Recall that according to Section 14.1, thermodynamic variables come in conjugate pairs. This means that the variable n ought to have a conjugate partner—some new variable we have not yet considered. What should be the properties of this hypothetical new variable? Assuming that It’s OK to be Lazy, the boxes in Section 14.1 practically define the new quantity for us. Let the chemical potential, , denote the thermodynamic variable con- jugate to n. Since n is extensive, must be intensive—with dimensions of energy per mole. The three conjugate pairs are thus (T, S), (P, V ) and (, n). One independent variable can be chosen from each pair—although in practice, n is almost always used from the last pair.
The thermodynamic variables and their key relationships are summarized in the box below; each row corresponds to a different conjugate pair:
Furthermore, with n now treated as a variable, we expect new, generalized total differentials for the thermodynamic potentials, of the following form:
Chemical Potential
From the discussion in Section 15.1—and especially the two boxes—the meaning of the chemical potential is now clear. Specifically, from the lower right corners of these two boxes, we obtain the following:
The extensivity of G implies G(T, P, n) = nGm(T, P). It thus follows from Definition 15.1 that = Gm. So why not take = Gm to be the definition— or simply dispense with altogether, and work with Gm instead? This strategy would only work for a pure substance in a single phase; in more general situations, and Gm are not equivalent [although Equation (15.1) always holds].
To understand the role that plays in diffusion, consider a system that is suddenly brought into diffusive contact with its surroundings. In perfect analogy with thermal and mechanical contact, ≠ sur implies a lack of diffusive equilibrium—leading to a spontaneous net flow of particles from high to low . This flow continues until = sur, and equilibrium is restored.
Just like for the other two types of equilibria, the above situation can be interpreted in entropic/information terms. In accord with Section 12.4, diffusive contact removes a macroscopic restriction on the system—i.e., the system is no longer closed. The system then takes advantage of its new freedom by exploring the expanded range of molecular states now available to it—i.e., particles migrate between the system and surroundings. This results in a macroscopic change of state—i.e., a change in the variable n. Macroscopic change continues until the total system entropy is maximized, at which point diffusive equilibrium is restored. It is the same basic thermodynamic dram reenacted yet again, but with a different cast of players…
⊳⊳⊳ To Ponder… Even after the system has reached diffusive equilibrium, particles continue to drift randomly in and out. Thus, N = N(t) is not strictly constant over time, but fluctuates—much like E(t) in Figure 5.1. In anal- ogy with U, then, the true thermodynamic quantity for open systems is actually ⟨(t) , rather than N itself. How- ever, many authors (including this one!) are “sloppy,” by using ‘N’ to denote both N and ⟨ (t) . In practice, the ⟩ two quantities are very nearly identical for sufficiently large systems—e.g., those of macroscopic, N ≈ NA proportions.
Ideal Gas & Fugacity
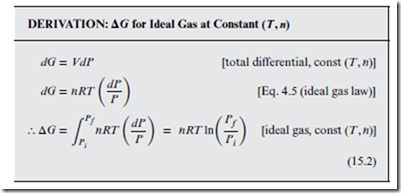
Consider the following derivation of ΔG, for an ideal gas under reversible expansion at constant (T, n):
Dividing Equation (15.2) by n results in a similar expression for the ideal gas isothermal Δ. This form is useful for relating the of a standard reference state (see Section 14.4), to some unknown at a different pressure. Specifically, taking Pf = P as the pressure of interest, and taking the initial state to be the standard reference state (Pi = P◦), we obtain the following:
Note that Equation (15.3) provides a simple relation between and P, for ideal gases. This relation is extremely important in practice, because it enables a determination of directly from P—which is typically much easier to measure in a laboratory experiment.
Of course, Equation (15.3) breaks down for non-ideal systems. Nevertheless, even in the non-ideal case, it would be convenient to work with some pressure-like quantity that does directly relate to . This motivates the following definition—for the fugacity, f , or “tendency to flee”:
Thus, f is what replaces P, to make Equation (15.3) true in the general, non-ideal case.
By design, fugacity has dimensions of pressure, and also f = P for the ideal gas. For non-ideal systems, f < P (or f > P) if attractive (or repulsive) intermolecular interactions dominate. Thus, fugacity plays a similar role to the compressibility factor, Z (p. 30), and the internal pressure, T (Section 9.3), in that it informs us the extent to which—and direction in which—a substance is non-ideal.
The main role of fugacity, however, is to serve as a pressure-like substitute for the chemical potential. In fact, Equation (15.4) implies that f = fsur is a valid condition for diffusive equilibrium (provided T = Tsur and P = Psur).
Most engineers (including chemical engineers!) prefer f to , particularly when applying these quantities to equilibrium phase transitions and mixtures (phase equilibria).
One minor weakness of the Equation (15.4) definition of fugacity is that it depends on the choice of reference state, and is therefore only a “relative” quantity. Physicists prefer to work with a dimensionless, “absolute” fugacity quantity, defined as exp(∕RT).
⊳⊳⊳ To Ponder…at a deeper level. The abso- lute fugacity has direct relevance for statistical mechanics—particularly for quantum statistical phenomena (e.g., Bose-Einstein condensation) whose onset occurs when exp(∕RT) ≈ 1 (see, e.g., Callen, Section 18-3).
The absolute fugacity is also called the absolute activity, by some authors.
It is closely related to the activity in solution chemistry, and to the fugacity coefficient in the study of phase equilibria—both of which are also dimensionless quantities. However, one important difference is that the latter are relative quantities, despite being dimensionless.