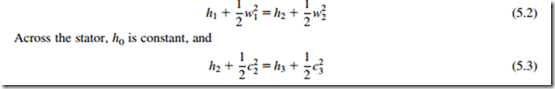Thermodynamics of the compressor stage
The specific work done by the rotor on the fluid, from the steady flow energy equation (assuming adiabatic flow) and momentum equation is
In Chapter 1, it was shown that the Euler work equation can be written as h0,rel 2 U2 5 constant. For axial machines where there is no radial shift of the streamlines across the rotor (i.e., U1 5 U2), then h0;rel 5 h 1 ð1=2Þw2 is constant in the rotor. Thus,
The compression process for the complete stage is represented on a Mollier diagram in Figure 5.3, which is generalized to include the effects of irreversibility.
Stage loss relationships and efficiency
From Eqs (5.1) and (5.3) the actual work performed by the rotor on unit mass of fluid is ΔW 5 h03 2 h01. Referring to Figure 5.3, the reversible or minimum work required to attain the same final stagnation pressure as the real process is
Applying the equation for the second law of thermodynamics, Tds 5 dh 2 dp/ρ, along the curve of constant pressure, p 5 p03, the approximation that Δh 5 TΔs can be used such that
Therefore, to determine the efficiency of the stage, we need to determine the entropy changes through the rotor and stator. This can be done by using the loss coefficients, Yp,rotor and Yp,stator, which are defined as
Consider the process of a perfect gas passing through the rotor at constant relative stagnation enthalpy, h01,rel (i.e., U1 5 U2). The second law of thermodynamics, T ds 5 dh 2 dp/ρ, can be writ- ten for this process as
Note that the negative sign in the T ds equation disappears since the relative stagnation pressure is decreasing through the rotor, giving an increase in entropy. Also note that a key advantage of using entropy here is that it is independent of the frame of reference in which it is evaluated. The entropy change through the stator is found similarly to that for the rotor, and the total entropy change through the stage is simply the sum of the two. In terms of the loss coefficients,
Hence, the total-to-total efficiency can be written as
For a low-speed machine, where the flow is incompressible as well as the density being constant, it can be assumed that temperature changes throughout the stage are negligible. Applying the second law equation, T ds 5 dh 2 dp/ρ, for the flow through the rotor and the stator then gives
Compressor loss sources
In a compressor stage, there are numerous loss sources that cause entropy creation. It is the sum of all the entropy creation in a blade row that determines the loss coefficients, Yp,rotor and Yp,stator, which are used in mean-line analysis to determine the efficiency in Eqs (5.10) and (5.12b). The discussion of the various loss sources for turbines given in Section 4.6 is, in general, also applicable to compressors. There are, however, some key differences that are covered later.
The loss sources can be categorized as 2D and 3D. The possible 2D loss sources are the same as for turbines: (i) the blade boundary layers, (ii) trailing edge mixing, (iii) flow separation, and (iv) shock waves. The total 2D loss for a compressor can be determined through cascade tests or 2D computational methods (see Chapter 3), but there are no general correlations that can be applied to all cases. All compressor blades will suffer from boundary layer and trailing edge mixing loss, and Section 3.5 shows how these losses are strongly dependent on the blade surface pressure distribution. Well-designed compressor blades should not suffer from flow separation losses at their design operating conditions. However, at off-design conditions, when the diffusion levels on the blade surfaces become too high, the flow can separate leading to excessive loss and possible stall or surge (see Section 5.11). Shock wave losses are only present in compressor stages with super- sonic inlet flow and these are discussed further in Section 5.10.
The main 3D loss sources in a compressor are (i) end wall loss, and (ii) tip leakage loss. However, in practice, it is difficult to isolate these loss sources as they interact strongly and the total 3D loss is often simply described as loss due to secondary flow.
Annulus boundary layers rapidly build up on the hub and casing of a compressor. As shown later in Section 5.9, these boundary layers are thicker than in a turbine due to the adverse pressure gradients they are exposed to. They are swept across the blade passage by the pressure difference between the pressure and the suction surfaces, leading to a complex and extensive 3D flow field. These end wall flows cause loss through viscous shear and through mixing with the mainstream flow in the blade passages. In addition, they interact with the boundary layers on the blade surfaces, potentially causing further loss. There have been several attempts to model and predict the loss caused by compressor end wall flow, see Koch and Smith (1976) for a more successful example. However, because the end wall boundary layers are large and the flow field is particular to each compressor stage, test results or advanced 3D computational methods are nowadays used to determine end wall loss.
The flow through the clearance gap above the tips of compressor rotor blades interacts with the end wall flow and the flow in the passage creating further loss through mixing and shear. The leak- age flow also causes blockage, reducing the overall flow capacity of the compressor stage and, more seriously, reduces the stable operating range, see Freeman (1985). The aim is always to mini- mize the clearance gap to improve the stability margin and to reduce the losses, but the minimum clearance is usually determined by manufacturing and mechanical considerations.
Leakage flows are not only found in the rotor tip gaps. Stator blades are often cantilevered from the compressor casing to minimize weight. This leads to a clearance gap at the stator hub. The leakage flow that arises can help relieve high diffusion at the stator hub, but it also adds to block- age and loss. In addition, leakage flows arise from any gaps or seals that are present in the real geometry of a compressor.
The 3D flows described earlier will typically contribute 50% or more of the losses within a compressor (the other 50% coming from the 2D loss). They also lead to reduced flow capacity due to the additional blockage, reduced work input, and more limited operating range. They need to be accounted for in the preliminary design by using average loss coefficients for the whole flow field and by factoring the velocity triangle parameters appropriately such that they represent the average flow conditions.
Note that 3D effects and secondary flows are covered in detail in Chapter 6. Further details of compressor loss sources can be found in Koch and Smith (1976) and Denton (1993).