Ohm’s law
The fundamental law of simple circuits was expressed by the Frenchman G. S. Ohm in the early 1800s in a paper on the effects of heat on resistance. The law takes three algebraic forms, each based on the following relationship: a potential of 1V drives 1A through a resistance of 1!1. In the equations the symbol E stands for electromo- tive force, or, as we now say, volts. An I represents intensity, or current, and R is resistance in ohms.
The basic relationship is expressed as:
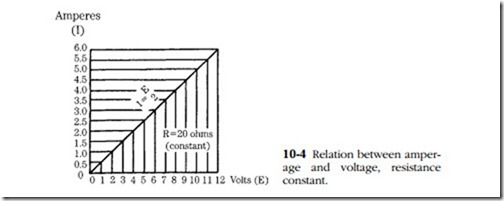
This form of the equation states that current in amperes equals voltage in volts divided by resistance in ohms. If a circuit with a resistance of 6!1, is connected across a 12V source, the current is 2A (12/6 2). Double the voltage (or halve the resis- tance), and the current doubles. Figure 10-4 shows this linear (straight-line graph) relationship.
Another form of Ohm’s law is
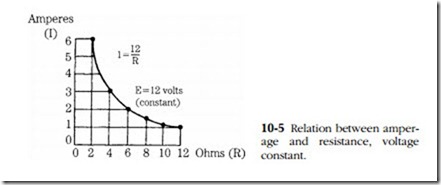
or resistance equals voltage divided by current. The 12V potential of our hypo- thetical circuit delivers 2A, which means the resistance is 6!1. The relationship between amperage and resistance with a constant voltage is illustrated in Fig. 10-5.
Another way of expressing Ohm’s law is
E = IR
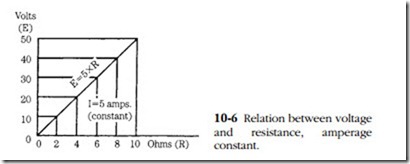
or voltage equals current multiplied by resistance. Two amperes through 6!1 requires a potential of 12V. Double the resistance, and twice the voltage is required to deliver the same amount of current (Fig. 10-6).
Various memory aids have been devised to help students remember Ohm’s law. One involves an Indian, an eagle, and a rabbit. The Indian (I ) sees the eagle (E ) fly- ing over the rabbit (R ); this gives the relationship I E /R. The eagle sees both the Indian and the rabbit in the same level, or E IR. And the rabbit sees the eagle over the Indian, or R E/I. A visual aid is shown in Fig. 10-7. The circle is divided into three segments. To determine which form of the equation to use, put your finger on the quantity you want to solve for.
All of this might seem academic, and in truth, few mechanics perform calculations with Ohm’s law. It is usually easier to measure all values directly with a meter. Still, it is very important to have an understanding of Ohm’s law. It is the best description of simple circuits we have.
For example, suppose the wiring is shorted: electrons have found a more direct (shorter) path to the positive terminal of the battery. Ohm’s law tells us certain facts about the nature of shorts, which are useful in troubleshooting. First, a short increases the current in the affected circuit, because current values respond inversely to resistance. This increase will generate heat in the conductor and might even car- bonize the insulation. Voltage readings will be low because the short has almost zero resistance. Now suppose we have a partially open circuit caused by a corroded ter- minal. The current through the terminal will be reduced, which means that the lights or whatever other load is on the circuit will operate at less-than-peak output. The terminal will be warm to the touch, because current is transformed to heat by the presence of resistance. Voltage readings from the terminal to ground will be high on the source side of the resistance and lower than normal past the bottleneck.