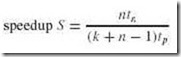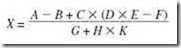The Essentials of Computer Organization and Architecture – A Closer Look at Instruction Set Architectures

Chapter 5: A Closer Look at Instruction Set Architectures

5.1 Introduction

“Every program has at least one bug and can be shortened by at least one instruction-from which, by induction, one can deduce that every program can be reduced to one instruction which doesn’t work.”

-Anonymous

We saw in Chapter 4 that machine instructions consist of opcodes and operands. The opcodes specify the operations to be executed; the operands specify register or memory locations of data. Why, when we have languages such as C++, Java, and Ada available, should we be concerned with machine instructions? When programming in a high-level language, we frequently have little awareness of the topics discussed in Chapter 4 (or in this chapter) because high-level languages hide the details of the architecture from the programmer. Employers frequently prefer to hire people with assembly language backgrounds not because they need an assembly language programmer, but because they need someone who can understand computer architecture to write more efficient and more effective programs.

In this chapter, we expand on the topics presented in the last chapter, the objective being to provide you with a more detailed look at machine instruction sets. We look at different instruction types and operand types, and how instructions access data in memory. You will see that the variations in instruction sets are integral in distinguishing different computer architectures. Understanding how instruction sets are designed and how they function can help you understand the more intricate details of the architecture of the machine itself.

5.2 Instruction Formats

We know that a machine instruction has an opcode and zero or more operands. In Chapter 4 we saw that MARIE had an instruction length of 16 bits and could have, at most, 1 operand. Encoding an instruction set can be done in a variety of ways. Architectures are differentiated from one another by the number of bits allowed per instruction (16, 32, and 64 are the most common), by the number of operands allowed per instruction, and by the types of instructions and data each can process. More specifically, instruction sets are differentiated by the following features:

• Operand storage in the CPU (data can be stored in a stack structure or in registers)

• Number of explicit operands per instruction (zero, one, two, and three being the most common)

• Operand location (instructions can be classified as register-to-register, register-to-memory or memory-to-memory, which simply refer to the combinations of operands allowed per instruction)

• Operations (including not only types of operations but also which instructions can access memory and which cannot)

• Type and size of operands (operands can be addresses, numbers, or even characters)

5.2.1 Design Decisions for Instruction Sets

When a computer architecture is in the design phase, the instruction set format must be determined before many other decisions can be made. Selecting this format is often quite difficult because the instruction set must match the architecture, and the architecture, if well designed, could last for decades. Decisions made during the design phase have long-lasting ramifications.

Instruction set architectures (ISAs) are measured by several different factors, including: (1) the amount of space a program requires; (2) the complexity of the instruction set, in terms of the amount of decoding necessary to execute an instruction, and the complexity of the tasks performed by the instructions; (3) the length of the instructions; and (4) the total number of instructions. Things to consider when designing an instruction set include:

• Short instructions are typically better because they take up less space in memory and can be fetched quickly. However, this limits the number of instructions, because there must be enough bits in the instruction to specify the number of instructions we need. Shorter instructions also have tighter limits on the size and number of operands.

• Instructions of a fixed length are easier to decode but waste space.

• Memory organization affects instruction format. If memory has, for example, 16 or 32-bit words and is not byte-addressable, it is difficult to access a single character. For this reason, even machines that have 16-, 32-, or 64-bit words are often byte-addressable, meaning every byte has a unique address even though words are longer than 1 byte.

• A fixed length instruction does not necessarily imply a fixed number of operands. We could design an ISA with fixed overall instruction length, but allow the number of bits in the operand field to vary as necessary. (This is called an expanding opcode and is covered in more detail in Section 5.2.5.)

• There are many different types of addressing modes. In Chapter 4, MARIE used two addressing modes: direct and indirect; however, we see in this chapter that a large variety of addressing modes exist.

• If words consist of multiple bytes, in what order should these bytes be stored on a byte-addressable machine? Should the least significant byte be stored at the highest or lowest byte address? This little versus big endian debate is discussed in the following section.

• How many registers should the architecture contain and how should these registers be organized? How should operands be stored in the CPU?

The little versus big endian debate, expanding opcodes, and CPU register organization are examined further in the following sections. In the process of discussing these topics, we also touch on the other design issues listed.

5.2.2 Little versus Big Endian

The term endian refers to a computer architecture’s “byte order,” or the way the computer stores the bytes of a multiple-byte data element. Virtually all computer architectures today are byte-addressable and must, therefore, have a standard for storing information requiring more than a single byte. Some machines store a two-byte integer, for example, with the least significant byte first (at the lower address) followed by the most significant byte. Therefore, a byte at a lower address has lower significance. These machines are called little endian machines. Other machines store this same two-byte integer with its most significant byte first, followed by its least significant byte. These are called big endian machines because they store the most significant bytes at the lower addresses. Most UNIX machines are big endian, whereas most PCs are little endian machines. Most newer RISC architectures are also big endian.

These two terms, little and big endian, are from the book Gulliver’s Travels. You may remember the story in which the Lilliputians (the tiny people) were divided into two camps: those who ate their eggs by opening the “big” end (big endians) and those who ate their eggs by opening the “little” end (little endians). CPU manufacturers are also divided into two factions. For example, Intel has always done things the “little endian” way whereas Motorola has always done things the “big endian” way. (It is also worth noting that some CPUs can handle both little and big endian.)

For example, consider an integer requiring 4 bytes:

On a little endian machine, this is arranged in memory as follows:

Base Address + 0 = Byte0

Base Address + 1 = Byte1
Base Address + 2 = Byte2
Base Address + 3 = Byte3

On a big endian machine, this long integer would then be stored as:

Base Address + 0 = Byte3
Base Address + 1 = Byte2
Base Address + 2 = Byte1
Base Address + 3 = Byte0

Let’s assume that on a byte-addressable machine, the 32-bit hex value 12345678 is stored at address 0. Each digit requires a nibble, so one byte holds two digits. This hex value is stored in memory as shown in Figure 5.1, where the shaded cells represent the actual contents of memory.

There are advantages and disadvantages to each method, although one method is not necessarily better than the other. Big endian is more natural to most people and thus makes it easier to read hex dumps. By having the high-order byte come first, you can always test whether the number is positive or negative by looking at the byte at offset zero. (Compare this to little endian where you must know how long the number is and then must skip over bytes to find the one containing the sign information.) Big endian machines store integers and strings in the same order and are faster in certain string operations. Most bitmapped graphics are mapped with a “most significant bit on the left” scheme, which means working with graphical elements larger than one byte can be handled by the architecture itself. This is a performance limitation for little endian computers because they must continually reverse the byte order when working with large graphical objects. When decoding compressed data encoded with such schemes as Huffman and LZW (discussed in Chapter 7), the actual codeword can be used as an index into a lookup table if it is stored in big endian (this is also true for encoding).

However, big endian also has disadvantages. Conversion from a 32-bit integer address to a 16-bit integer address requires a big endian machine to perform addition. High-precision arithmetic on little endian machines is faster and easier. Most architectures using the big endian scheme do not allow words to be written on non-word address boundaries (for example, if a word is 2 or 4 bytes, it must always begin on an even-numbered byte address). This wastes space. Little endian architectures, such as Intel, allow odd address reads and writes, which makes programming on these machines much easier. If a programmer writes an instruction to read a value of the wrong word size, on a big endian machine it is always read as an incorrect value; on a little endian machine, it can sometimes result in the correct data being read. (Note that Intel finally has added an instruction to reverse the byte order within registers.)

Computer networks are big endian, which means that when little endian computers are going to pass integers over the network (network device addresses, for example), they need to convert them to network byte order. Likewise, when they receive integer values over the network, they need to convert them back to their own native representation.

Although you may not be familiar with this little versus big endian debate, it is important to many current software applications. Any program that writes data to or reads data from a file must be aware of the byte ordering on the particular machine. For example, the Windows BMP graphics format was developed on a little endian machine, so to view BMPs on a big endian machine, the application used to view them must first reverse the byte order. Software designers of popular software are well aware of these byte-ordering issues. For example, Adobe Photoshop uses big endian, GIF is little endian, JPEG is big endian, MacPaint is big endian, PC Paintbrush is little endian, RTF by Microsoft is little endian, and Sun raster files are big endian. Some applications support both formats: Microsoft WAV and AVI files, TIFF files, and XWD (X windows Dump) support both, typically by encoding an identifier into the file.

5.2.3 Internal Storage in the CPU – Stacks versus Registers

Once byte ordering in memory is determined, the hardware designer must make some decisions on how the CPU should store data. This is the most basic means to differentiate ISAs. There are three choices:

1. A stack architecture

2. An accumulator architecture

3. A general purpose register (GPR) architecture

Stack architectures use a stack to execute instructions, and the operands are (implicitly) found on top of the stack. Even though stack-based machines have good code density and a simple model for evaluation of expressions, a stack cannot be accessed randomly, which makes it difficult to generate efficient code. Accumulator architectures such as MARIE, with one operand implicitly in the accumulator, minimize the internal complexity of the machine and allow for very short instructions. But because the accumulator is only temporary storage, memory traffic is very high. General purpose register architectures, which use sets of general purpose registers, are the most widely accepted models for machine architectures today. These register sets are faster than memory, easy for compilers to deal with, and can be used very effectively and efficiently. In addition, hardware prices have decreased significantly, making it possible to add a large number of registers at a minimal cost. If memory access is fast, a stack-based design may be a good idea; if memory is slow, it is often better to use registers. These are the reasons why most computers over the past 10 years have been general-register based. However, because all operands must be named, using registers results in longer instructions, causing longer fetch and decode times. (A very important goal for ISA designers is short instructions.) Designers choosing an ISA must decide which will work best in a particular environment and examine the tradeoffs carefully.

The general-purpose architecture can be broken into three classifications, depending on where the operands are located. Memory-memory architectures may have two or three operands in memory, allowing an instruction to perform an operation without requiring any operand to be in a register. Register-memory architectures require a mix, where at least one operand is in a register and one is in memory. Load-store architectures require data to be moved into registers before any operations on that data are performed. Intel and Motorola are examples of register-memory architectures; Digital Equipment’s VAX architecture allows memory-memory operations; and SPARC, MIPS, ALPHA, and the PowerPC are all load-store machines.

Given that most architectures today are GPR-based, we now examine two major instruction set characteristics that divide general-purpose register architectures. Those two characteristics are the number of operands and how the operands are addressed. In Section 5.2.4 we look at the instruction length and number of operands an instruction can have. (Two or three operands are the most common for GPR architectures, and we compare these to zero and one operand architectures.) We then investigate instruction types. Finally, in Section 5.4 we investigate the various addressing modes available.

5.2.4 Number of Operands and Instruction Length

The traditional method for describing a computer architecture is to specify the maximum number of operands, or addresses, contained in each instruction. This has a direct impact on the length of the instruction itself. MARIE uses a fixed-length instruction with a 4-bit opcode and a 12-bit operand. Instructions on current architectures can be formatted in two ways:

• Fixed length-Wastes space but is fast and results in better performance when instruction-level pipelining is used, as we see in Section 5.5.

• Variable length-More complex to decode but saves storage space.

Typically, the real-life compromise involves using two to three instruction lengths, which provides bit patterns that are easily distinguishable and simple to decode. The instruction length must also be compared to the word length on the machine. If the instruction length is exactly equal to the word length, the instructions align perfectly when stored in main memory. Instructions always need to be word aligned for addressing reasons. Therefore, instructions that are half, quarter, double, or triple the actual word size can waste space. Variable length instructions are clearly not the same size and need to be word aligned, resulting in loss of space as well.

The most common instruction formats include zero, one, two, or three operands. We saw in Chapter 4 that some instructions for MARIE have no operands, whereas others have one operand. Arithmetic and logic operations typically have two operands, but can be executed with one operand (as we saw in MARIE), if the accumulator is implicit. We can extend this idea to three operands if we consider the final destination as a third operand. We can also use a stack that allows us to have zero operand instructions. The following are some common instruction formats:

• OPCODE only (zero addresses)

• OPCODE + 1 Address (usually a memory address)

• OPCODE + 2 Addresses (usually registers, or one register and one memory address)

• OPCODE + 3 Addresses (usually registers, or combinations of registers and memory)

All architectures have a limit on the maximum number of operands allowed per instruction. For example, in MARIE, the maximum was one, although some instructions had no operands (Halt and Skipcond). We mentioned that zero-, one-, two-, and three-operand instructions are the most common. One-, two-, and even three-operand instructions are reasonably easy to understand; an entire ISA built on zero-operand instructions can, at first, be somewhat confusing.

Machine instructions that have no operands must use a stack (the last-in, first-out data structure, introduced in Chapter 4 and described in detail in Appendix A, where all insertions and deletions are made from the top) to perform those operations that logically require one or two operands (such as an Add). Instead of using general purpose registers, a stack-based architecture stores the operands on the top of the stack, making the top element accessible to the CPU. (Note that one of the most important data structures in machine architectures is the stack. Not only does this structure provide an efficient means of storing intermediate data values during complex calculations, but it also provides an efficient method for passing parameters during procedure calls as well as a means to save local block structure and define the scope of variables and subroutines.)

In architectures based on stacks, most instructions consist of opcodes only; however, there are special instructions (those that add elements to and remove elements from the stack) that have just one operand. Stack architectures need a push instruction and a pop instruction, each of which is allowed one operand. Push X places the data value found at memory location X onto the stack; Pop X removes the top element in the stack and stores it at location X. Only certain instructions are allowed to access memory; all others must use the stack for any operands required during execution.

For operations requiring two operands, the top two elements of the stack are used. For example, if we execute an Add instruction, the CPU adds the top two elements of the stack, popping them both and then pushing the sum onto the top of the stack. For noncommutative operations such as subtraction, the top stack element is subtracted from the next-to-the-top element, both are popped, and the result is pushed onto the top of the stack.

This stack organization is very effective for evaluating long arithmetic expressions written in (RPN). This representation places the operator after the operands in what is known as postfix notation (as compared to infix notation, which places the operator between operands, and prefix notation, which places the operator before the operands). For example:

X + Y is in infix notation

+ X Y is in prefix notation

X Y + is in postfix notation

All arithmetic expressions can be written using any of these representations. However, postfix representation combined with a stack of registers is the most efficient means to evaluate arithmetic expressions. In fact, some electronic calculators (such as Hewlett-Packard) require the user to enter expressions in postfix notation. With a little practice on these calculators, it is possible to rapidly evaluate long expressions containing many nested parentheses without ever stopping to think about how terms are grouped.

Consider the following expression:

(X + Y) x (W – Z) + 2

Written in RPN, this becomes:

XY + WZ – x2+

Notice that the need for parentheses to preserve precedence is eliminated when using RPN.

To illustrate the concepts of zero, one, two, and three operands, let’s write a simple program to evaluate an arithmetic expression, using each of these formats.

Example 5.1:

Suppose we wish to evaluate the following expression:

Z = (X x Y) + (W x U)

Typically, when three operands are allowed, at least one operand must be a register, and the first operand is normally the destination. Using three-address instructions, the code to evaluate the expression for Z is written as follows:

Mult    R1, X, Y
Mult    R2, W, U
Add    Z, R2, R1

When using two-address instructions, normally one address specifies a register (two-address instructions seldom allow for both operands to be memory addresses). The other operand could be either a register or a memory address. Using two-address instructions, our code becomes:

Load    R1, X
Mult    R1, Y
Load    R2, W
Mult    R2, U
Add    R1, R2
Store    Z, R1

Note that it is important to know whether the first operand is the source or the destination. In the above instructions, we assume it is the destination. (This tends to be a point of confusion for those programmers who must switch between Intel assembly language and Motorola assembly language-Intel assembly specifies the first operand as the destination, whereas in Motorola assembly, the first operand is the source.)

Using one-address instructions (as in MARIE), we must assume a register (normally the accumulator) is implied as the destination for the result of the instruction. To evaluate Z, our code now becomes:

Load    X
Mult    Y
Store    Temp
Load    W
Mult    U
Add    Temp
Store    Z

Note that as we reduce the number of operands allowed per instruction, the number of instructions required to execute the desired code increases. This is an example of a typical space/time trade-off in architecture design-shorter instructions but longer programs.

What does this program look like on a stack-based machine with zero-address instructions? Stack-based architectures use no operands for instructions such as Add, Subt, Mult, or Divide. We need a stack and two operations on that stack: Pop and Push. Operations that communicate with the stack must have an address field to specify the operand to be popped or pushed onto the stack (all other operations are zero-address). Push places the operand on the top of the stack. Pop removes the stack top and places it in the operand. This architecture results in the longest program to evaluate our equation. Assuming arithmetic operations use the two operands on the stack top, pop them, and push the result of the operation, our code is as follows:

Push    X
Push    Y
Mult
Push    W
Push    U
Mult
Add
Store    Z

The instruction length is certainly affected by the opcode length and by the number of operands allowed in the instruction. If the opcode length is fixed, decoding is much easier. However, to provide for backward compatibility and flexibility, opcodes can have variable length. Variable length opcodes present the same problems as variable versus constant length instructions. A compromise used by many designers is expanding opcodes.

5.2.5 Expanding Opcodes

Expanding opcodes represent a compromise between the need for a rich set of opcodes and the desire to have short opcodes, and thus short instructions. The idea is to make some opcodes short, but have a means to provide longer ones when needed. When the opcode is short, a lot of bits are left to hold operands (which means we could have two or three operands per instruction). When you don’t need any space for operands (for an instruction such as Halt or because the machine uses a stack), all the bits can be used for the opcode, which allows for many unique instructions. In between, there are longer opcodes with fewer operands as well as shorter opcodes with more operands.

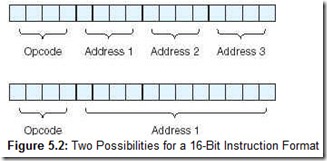
Consider a machine with 16-bit instructions and 16 registers. Because we now have a register set instead of one simple accumulator (as in MARIE), we need to use 4 bits to specify a unique register. We could encode 16 instructions, each with 3 register operands (which implies any data to be operated on must first be loaded into a register), or use 4 bits for the opcode and 12 bits for a memory address (as in MARIE, assuming a memory of size 4K). Any memory reference requires 12 bits, leaving only 4 bits for other purposes. However, if all data in memory is first loaded into a register in this register set, the instruction can select that particular data element using only 4 bits (assuming 16 registers). These two choices are illustrated in Figure 5.2.

Suppose we wish to encode the following instructions:

• 15 instructions with 3 addresses

• 14 instructions with 2 addresses

• 31 instructions with 1 address

• 16 instructions with 0 addresses

Can we encode this instruction set in 16 bits? The answer is yes, as long as we use expanding opcodes. The encoding is as follows:

This expanding opcode scheme makes the decoding more complex. Instead of simply looking at a bit pattern and deciding which instruction it is, we need to decode the instruction something like this:

if (leftmost four bits != 1111 ) {
  Execute appropriate three-address instruction}
else if (leftmost seven bits != 1111 111 ) {
  Execute appropriate two-address instruction}
else if (leftmost twelve bits != 1111 1111 1111 ) {
  Execute appropriate one-address instruction }
else {
  Execute appropriate zero-address instruction
}

At each stage, one spare code is used to indicate that we should now look at more bits. This is another example of the types of trade-offs hardware designers continually face: Here, we trade opcode space for operand space.

5.3 Instruction Types

Most computer instructions operate on data; however, there are some that do not. Computer manufacturers regularly group instructions into the following categories:

• Data movement

• Arithmetic

• Boolean

• Bit manipulation (shift and rotate)

• I/O

• Transfer of control

• Special purpose

Data movement instructions are the most frequently used instructions. Data is moved from memory into registers, from registers to registers, and from registers to memory, and many machines provide different instructions depending on the source and destination. For example, there may be a MOVER instruction that always requires two register operands, whereas a MOVE instruction allows one register and one memory operand. Some architectures, such as RISC, limit the instructions that can move data to and from memory in an attempt to speed up execution. Many machines have variations of load, store, and move instructions to handle data of different sizes. For example, there may be a LOADB instruction for dealing with bytes and a LOADW instruction for handling words.

Arithmetic operations include those instructions that use integers and floating point numbers. Many instruction sets provide different arithmetic instructions for various data sizes. As with the data movement instructions, there are sometimes different instructions for providing various combinations of register and memory accesses in different addressing modes.

Boolean logic instructions perform Boolean operations, much in the same way that arithmetic operations work. There are typically instructions for performing AND, NOT, and often OR and XOR operations.

Bit manipulation instructions are used for setting and resetting individual bits (or sometimes groups of bits) within a given data word. These include both arithmetic and logical shift instructions and rotate instructions, both to the left and to the right. Logical shift instructions simply shift bits to either the left or the right by a specified amount, shifting in zeros from the opposite end. Arithmetic shift instructions, commonly used to multiply or divide by 2, do not shift the leftmost bit, because this represents the sign of the number. On a right arithmetic shift, the sign bit is replicated into the bit position to its right. On a left arithmetic shift, values are shifted left, zeros are shifted in, but the sign bit is never moved. Rotate instructions are simply shift instructions that shift in the bits that are shifted out. For example, on a rotate left 1 bit, the leftmost bit is shifted out and rotated around to become the rightmost bit.

I/O instructions vary greatly from architecture to architecture. The basic schemes for handling I/O are programmed I/O, interrupt-driven I/O, and DMA devices. These are covered in more detail in Chapter 7.

Control instructions include branches, skips, and procedure calls. Branching can be unconditional or conditional. Skip instructions are basically branch instructions with implied addresses. Because no operand is required, skip instructions often use bits of the address field to specify different situations (recall the Skipcond instruction used by MARIE). Procedure calls are special branch instructions that automatically save the return address. Different machines use different methods to save this address. Some store the address at a specific location in memory, others store it in a register, while still others push the return address on a stack. We have already seen that stacks can be used for other purposes.

Special purpose instructions include those used for string processing, high-level language support, protection, flag control, and cache management. Most architectures provide instructions for string processing, including string manipulation and searching.

5.4 Addressing

Although addressing is an instruction design issue and is technically part of the instruction format, there are so many issues involved with addressing that it merits its own section. We now present the two most important of these addressing issues: the types of data that can be addressed and the various addressing modes. We cover only the fundamental addressing modes; more specialized modes are built using the basic modes in this section.

5.4.1 Data Types

Before we look at how data is addressed, we will briefly mention the various types of data an instruction can access. There must be hardware support for a particular data type if the instruction is to reference that type. In Chapter 2 we discussed data types, including numbers and characters. Numeric data consists of integers and floating point values. Integers can be signed or unsigned and can be declared in various lengths. For example, in C++ integers can be short (16 bits), int (the word size of the given architecture), or long (32 bits). Floating point numbers have lengths of 32, 64, or 128 bits. It is not uncommon for ISAs to have special instructions to deal with numeric data of varying lengths, as we have seen earlier. For example, there might be a MOVE for 16-bit integers and a different MOVE for 32-bit integers.

Nonnumeric data types consist of strings, Booleans, and pointers. String instructions typically include operations such as copy, move, search, or modify. Boolean operations include AND, OR, XOR, and NOT. Pointers are actually addresses in memory. Even though they are, in reality, numeric in nature, pointers are treated differently than integers and floating point numbers. MARIE allows for this data type by using the indirect addressing mode. The operands in the instructions using this mode are actually pointers. In an instruction using a pointer, the operand is essentially an address and must be treated as such.

5.4.2 Address Modes

We saw in Chapter 4 that the 12 bits in the operand field of a MARIE instruction can be interpreted in two different ways: the 12 bits represent either the memory address of the operand or a pointer to a physical memory address. These 12 bits can be interpreted in many other ways, thus providing us with several different addressing modes. Addressing modes allow us to specify where the instruction operands are located. An addressing mode can specify a constant, a register, or a location in memory. Certain modes allow shorter addresses and some allow us to determine the location of the actual operand, often called the effective address of the operand, dynamically. We now investigate the most basic addressing modes.

Immediate Addressing

Immediate addressing is so-named because the value to be referenced immediately follows the operation code in the instruction. That is to say, the data to be operated on is part of the instruction. For example, if the addressing mode of the operand is immediate and the instruction is Load 008, the numeric value 8 is loaded into the AC. The 12 bits of the operand field do not specify an address-they specify the actual operand the instruction requires. Immediate addressing is very fast because the value to be loaded is included in the instruction. However, because the value to be loaded is fixed at compile time it is not very flexible.

Direct Addressing

Direct addressing is so-named because the value to be referenced is obtained by specifying its memory address directly in the instruction. For example, if the addressing mode of the operand is direct and the instruction is Load 008, the data value found at memory address 008 is loaded into the AC. Direct addressing is typically quite fast because, although the value to be loaded is not included in the instruction, it is quickly accessible. It is also much more flexible than immediate addressing because the value to be loaded is whatever is found at the given address, which may be variable.

Register Addressing

In register addressing, a register, instead of memory, is used to specify the operand. This is very similar to direct addressing, except that instead of a memory address, the address field contains a register reference. The contents of that register are used as the operand.

Indirect Addressing

Indirect addressing is a very powerful addressing mode that provides an exceptional level of flexibility. In this mode, the bits in the address field specify a memory address that is to be used as a pointer. The effective address of the operand is found by going to this memory address. For example, if the addressing mode of the operand is indirect and the instruction is Load 008, the data value found at memory address 008 is actually the effective address of the desired operand. Suppose we find the value 2A0 stored in location 008. 2A0 is the “real” address of the value we want. The value found at location 2A0 is then loaded into the AC.

In a variation on this scheme, the operand bits specify a register instead of a memory address. This mode, known as register indirect addressing, works exactly the same way as indirect addressing mode, except it uses a register instead of a memory address to point to the data. For example, if the instruction is Load R1 and we are using register indirect addressing mode, we would find the effective address of the desired operand in R1.

Indexed and Based Addressing

In indexed addressing mode, an index register (either explicitly or implicitly designated) is used to store an offset (or displacement), which is added to the operand, resulting in the effective address of the data. For example, if the operand X of the instruction Load X is to be addressed using indexed addressing, assuming R1 is the index register and holds the value 1, the effective address of the operand is actually X + 1. Based addressing mode is similar, except a base address register, rather than an index register, is used. In theory, the difference between these two modes is in how they are used, not how the operands are computed. An index register holds an index that is used as an offset, relative to the address given in the address field of the instruction. A base register holds a base address, where the address field represents a displacement from this base. These two addressing modes are quite useful for accessing array elements as well as characters in strings. In fact, most assembly languages provide special index registers that are implied in many string operations. Depending on the instruction-set design, general-purpose registers may also be used in this mode.

Stack Addressing

If stack addressing mode is used, the operand is assumed to be on the stack. We have already seen how this works in Section 5.2.4.

Additional Addressing Modes

Many variations on the above schemes exist. For example, some machines have indirect indexed addressing, which uses both indirect and indexed addressing at the same time. There is also base/offset addressing, which adds an offset to a specific base register and then adds this to the specified operand, resulting in the effective address of the actual operand to be used in the instruction. There are also auto-increment and auto-decrement modes. These modes automatically increment or decrement the register used, thus reducing the code size, which can be extremely important in applications such as embedded systems. Self-relative addressing computes the address of the operand as an offset from the current instruction. Additional modes exist; however, familiarity with immediate, direct, register, indirect, indexed, and stack addressing modes goes a long way in understanding any addressing mode you may encounter.

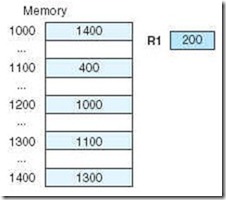
Let’s look at an example to illustrate these various modes. Suppose we have the instruction Load 800, and the memory and register R1 shown in Figure 5.3.

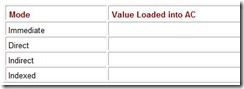
Applying the various addressing modes to the operand field containing the 800, and assuming R1 is implied in the indexed addressing mode, the value actually loaded into AC is seen in Table 5.1.

Table 5.1: Results of Using Various Addressing Modes on Memory in Figure 5.2

The instruction Load R1, using register addressing mode, loads an 800 into the accumulator, and using register indirect addressing mode, loads a 900 into the accumulator.

We summarize the addressing modes in Table 5.2.

Table 5.2: A Summary of the Basic Addressing Modes

The various addressing modes allow us to specify a much larger range of locations than if we were limited to using one or two modes. As always, there are trade-offs. We sacrifice simplicity in address calculation and limited memory references for flexibility and increased address range.

5.5 Instruction-Level Pipelining

By now you should be reasonably familiar with the fetch-decode-execute cycle presented in Chapter 4. Conceptually, each pulse of the computer’s clock is used to control one step in the sequence, but sometimes additional pulses can be used to control smaller details within one step. Some CPUs break the fetch-decode-execute cycle down into smaller steps, where some of these smaller steps can be performed in parallel. This overlapping speeds up execution. This method, used by all current CPUs, is known as pipelining.

Suppose the fetch-decode-execute cycle were broken into the following “mini-steps”:

1. Fetch instruction

2. Decode opcode

3. Calculate effective address of operands

4. Fetch operands

5. Execute instruction

6. Store result

Pipelining is analogous to an automobile assembly line. Each step in a computer pipeline completes a part of an instruction. Like the automobile assembly line, different steps are completing different parts of different instructions in parallel. Each of the steps is called a pipeline stage. The stages are connected to form a pipe. Instructions enter at one end, progress through the various stages, and exit at the other end. The goal is to balance the time taken by each pipeline stage (i.e., more or less the same as the time taken by any other pipeline stage). If the stages are not balanced in time, after awhile, faster stages will be waiting on slower ones. To see an example of this imbalance in real life, consider the stages of doing laundry. If you have only one washer and one dryer, you usually end up waiting on the dryer. If you consider washing as the first stage and drying as the next, you can see that the longer drying stage causes clothes to pile up between the two stages. If you add folding clothes as a third stage, you soon realize that this stage would consistently be waiting on the other, slower stages.

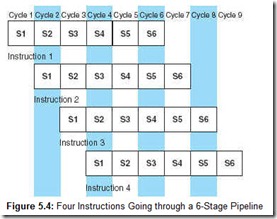
Figure 5.4 provides an illustration of computer pipelining with overlapping stages. We see each clock cycle and each stage for each instruction (where S1 represents the fetch, S2 represents the decode, S3 is the calculate state, S4 is the operand fetch, S5 is the execution, and S6 is the store).

We see from Figure 5.4 that once instruction 1 has been fetched and is in the process of being decoded, we can start the fetch on instruction 2. When instruction 1 is fetching operands, and instruction 2 is being decoded, we can start the fetch on instruction 3. Notice these events can occur in parallel, very much like an automobile assembly line.

Suppose we have a k-stage pipeline. Assume the clock cycle time is t_p, that is, it takes t_p time per stage. Assume also we have n instructions (often called tasks) to process. Task 1 (T₁) requires k x t_p time to complete. The remaining n – 1 tasks emerge from the pipeline one per cycle, which implies a total time for these tasks of (n – 1)t_p. Therefore, to complete n tasks using a k-stage pipeline requires:

(k x t_p) + (n – 1)t_p = (k + n – 1)t_p

or k + (n – 1) clock cycles.

Let’s calculate the speedup we gain using a pipeline. Without a pipeline, the time required is nt_n cycles, where t_n = k x t_p. Therefore, the speedup (time without a pipeline divided by the time using a pipeline) is:

If we take the limit of this as n approaches infinity, we see that (k + n – 1) approaches n, which results in a theoretical speedup of:

The theoretical speedup, k, is the number of stages in the pipeline.

Let’s look at an example. Suppose we have a 4-stage pipeline, where:

• S1 = fetch instruction

• S2 = decode and calculate effective address

• S3 = fetch operand

• S4 = execute instruction and store results

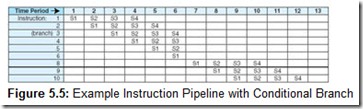
We must also assume the architecture provides a means to fetch data and instructions in parallel. This can be done with separate instruction and data paths; however, most memory systems do not allow this. Instead, they provide the operand in cache, which, in most cases, allows the instruction and operand to be fetched simultaneously. Suppose, also, that instruction I3 is a conditional branch statement that alters the execution sequence (so that instead of I4 running next, it transfers control to I8). This results in the pipeline operation shown in Figure 5.5.

Note that I4, I5, and I6 are fetched and proceed through various stages, but after the execution of I3 (the branch), I4, I5, and I6 are no longer needed. Only after time period 6, when the branch has executed, can the next instruction to be executed (I8) be fetched, after which, the pipe refills. From time periods 6 through 9, only one instruction has executed. In a perfect world, for each time period after the pipe originally fills, one instruction should flow out of the pipeline. However, we see in this example that this is not necessarily true.

Please note that not all instructions must go through each stage of the pipe. If an instruction has no operand, there is no need for stage 3. To simplify pipelining hardware and timing, all instructions proceed through all stages, whether necessary or not.

From our preceding discussion of speedup, it might appear that the more stages that exist in the pipeline, the faster everything will run. This is true to a point. There is a fixed overhead involved in moving data from memory to registers. The amount of control logic for the pipeline also increases in size proportional to the number of stages, thus slowing down total execution. In addition, there are several conditions that result in “pipeline conflicts,” which keep us from reaching the goal of executing one instruction per clock cycle. These include:

• Resource conflicts

• Data dependencies

• Conditional branch statements

Resource conflicts are a major concern in instruction-level parallelism. For example, if one instruction is storing a value to memory while another is being fetched from memory, both need access to memory. Typically this is resolved by allowing the instruction executing to continue, while forcing the instruction fetch to wait. Certain conflicts can also be resolved by providing two separate pathways: one for data coming from memory and another for instructions coming from memory.

Data dependencies arise when the result of one instruction, not yet available, is to be used as an operand to a following instruction. There are several ways to handle these types of pipeline conflicts. Special hardware can be added to detect instructions whose source operands are destinations for instructions further up the pipeline. This hardware can insert a brief delay (typically a no-op instruction that does nothing) into the pipeline, allowing enough time to pass to resolve the conflict. Specialized hardware can also be used to detect these conflicts and route data through special paths that exist between various stages of the pipeline. This reduces the time necessary for the instruction to access the required operand. Some architectures address this problem by letting the compiler resolve the conflict. Compilers have been designed that reorder instructions, resulting in a delay of loading any conflicting data but having no effect on the program logic or output.

Branch instructions allow us to alter the flow of execution in a program, which, in terms of pipelining, causes major problems. If instructions are fetched one per clock cycle, several can be fetched and even decoded before a preceding instruction, indicating a branch, is executed. Conditional branching is particularly difficult to deal with. Many architectures offer branch prediction, using logic to make the best guess as to which instructions will be needed next (essentially, they are predicting the outcome of a conditional branch). Compilers try to resolve branching issues by rearranging the machine code to cause a delayed branch. An attempt is made to reorder and insert useful instructions, but if that is not possible, no-op instructions are inserted to keep the pipeline full. Another approach used by some machines given a conditional branch is to start fetches on both paths of the branch and save them until the branch is actually executed, at which time the “true” execution path will be known.

In an effort to squeeze even more performance out of the chip, modern CPUs employ superscalar design (introduced in Chapter 4), which is one step beyond pipelining. Superscalar chips have multiple ALUs and issue more than one instruction in each clock cycle. The clock cycles per instruction can actually go below one. But the logic to keep track of hazards becomes even more complex; more logic is needed to schedule operations than to do them. But even with complex logic, it is hard to schedule parallel operations “on the fly.”

The limits of dynamic scheduling have led machine designers to consider a very different architecture, explicitly parallel instruction computers (EPIC), exemplified by the Itanium architecture discussed in Chapter 4. EPIC machines have very large instructions (recall the instructions for the Itanium are 128 bits), which specify several operations to be done in parallel. Because of the parallelism inherent in the design, the EPIC instruction set is heavily compiler dependent (which means a user needs a sophisticated compiler to take advantage of the parallelism to gain significant performance advantages). The burden of scheduling operations is shifted from the processor to the compiler, and much more time can be spent in developing a good schedule and analyzing potential pipeline conflicts.

To reduce the pipelining problems due to conditional branches, the IA-64 introduced predicated instructions. Comparison instructions set predicate bits, much like they set condition codes on the x86 machine (except that there are 64 predicate bits). Each operation specifies a predicate bit; it is executed only if the predicate bit equals 1. In practice, all operations are performed, but the result is stored into the register file only if the predicate bit equals 1. The result is that more instructions are executed, but we don’t have to stall the pipeline waiting for a condition.

There are several levels of parallelism, varying from the simple to the more complex. All computers exploit parallelism to some degree. Instructions use words as operands (where words are typically 16, 32, or 64 bits in length), rather than acting on single bits at a time. More advanced types of parallelism require more specific and complex hardware and operating system support.

Although an in-depth study of parallelism is beyond the scope of this text, we would like to take a brief look at what we consider the two extremes of parallelism: program level parallelism (PLP) and instruction level parallelism (ILP). PLP actually allows parts of a program to run on more than one computer. This may sound simple, but it requires coding the algorithm correctly so that this parallelism is possible, in addition to providing careful synchronization between the various modules.

ILP involves the use of techniques to allow the execution of overlapping instructions. Essentially, we want to allow more than one instruction within a single program to execute concurrently. There are two kinds of ILP. The first type decomposes an instruction into stages and overlaps these stages. This is exactly what pipelining does. The second kind of ILP allows individual instructions to overlap (that is, instructions can be executed at the same time by the processor itself).

In addition to pipelined architectures, superscalar, superpipelining, and very long instruction word (VLIW) architectures exhibit ILP. Superscalar architectures (as you may recall from Chapter 4) perform multiple operations at the same time by employing parallel pipelines. Examples of superscalar architectures include IBM’s PowerPC, Sun’s UltraSparc, and DEC’s Alpha. Superpipelining architectures combine superscalar concepts with pipelining, by dividing the pipeline stages into smaller pieces. The IA-64 architecture exhibits a VLIW architecture, which means each instruction can specify multiple scalar operations (the compiler puts multiple operations into a single instruction). Superscalar and VLIW machines fetch and execute more than one instruction per cycle.

5.6 Real-World Examples of ISAs

Let’s return to the two architectures we discussed in Chapter 4, Intel and MIPS, to see how the designers of these processors chose to deal with the issues introduced in this chapter: instruction formats, instruction types, number of operands, addressing, and pipelining. We’ll also introduce the Java Virtual Machine to illustrate how software can create an ISA abstraction that completely hides the real ISA of the machine.

5.6.1 Intel

Intel uses a little endian, two-address architecture, with variable-length instructions. Intel processors use a register-memory architecture, which means all instructions can operate on a memory location, but the other operand must be a register. This ISA allows variable-length operations, operating on data with lengths of 1, 2, or 4 bytes.

The 8086 through the 80486 are single-stage pipeline architectures. The architects reasoned that if one pipeline was good, two would be better. The Pentium had two parallel five-stage pipelines, called the U pipe and the V pipe, to execute instructions. Stages for these pipelines include Prefetch, Instruction Decode, Address Generation, Execute, and Write Back. To be effective, these pipelines must be kept filled, which requires instructions that can be issued in parallel. It is the compiler’s responsibility to make sure this parallelism happens. The Pentium II increased the number of stages to 12, including Prefetch, Length Decode, Instruction Decode, Rename/Resource Allocation, UOP Scheduling/Dispatch, Execution, Write Back, and Retirement. Most of the new stages were added to address Intel’s MMX technology, an extension to the architecture that handles multimedia data. The Pentium III increased the stages to 14, and the Pentium IV to 24. Additional stages (beyond those introduced in this chapter) included stages for determining the length of the instruction, stages for creating microoperations, and stages to “commit” the instruction (make sure it executes and the results become permanent). The Itanium contains only a 10-stage instruction pipeline.

Intel processors allow for the basic addressing modes introduced in this chapter, in addition to many combinations of those modes. The 8086 provided 17 different ways to access memory, most of which were variants of the basic modes. Intel’s more current Pentium architectures include the same addressing modes as their predecessors, but also introduce new modes, mostly to help with maintaining backward compatibility. The IA-64 is surprisingly lacking in memory-addressing modes. It has only one: register-indirect (with optional post-increment). This seems unusually limiting but follows the RISC philosophy. Addresses are calculated and stored in general-purpose registers. The more complex addressing modes require specialized hardware; by limiting the number of addressing modes, the IA-64 architecture minimizes the need for this specialized hardware.

5.6.2 MIPS

The MIPS architecture (which originally stood for “Microprocessor without Interlocked Pipeline Stages”) is a little endian, word-addressable, three-address, fixed-length ISA. This is a load and store architecture, which means only the load and store instructions can access memory. All other instructions must use registers for operands, which implies that this ISA needs a large register set. MIPS is also limited to fixed-length operations (those that operate on data with the same number of bytes).

Some MIPS processors (such as the R2000 and R3000) have five-stage pipelines. The R4000 and R4400 have 8-stage superpipelines. The R10000 is quite interesting in that the number of stages in the pipeline depends on the functional unit through which the instruction must pass: there are five stages for integer instructions, six for load/store instructions, and seven for floating-point instructions. Both the MIPS 5000 and 10000 are superscalar.

MIPS has a straightforward ISA with five basic types of instructions: simple arithmetic (add, XOR, NAND, shift), data movement (load, store, move), control (branch, jump), multi-cycle (multiply, divide), and miscellaneous instructions (save PC, save register on condition). MIPS programmers can use immediate, register, direct, indirect register, base, and indexed addressing modes. However, the ISA itself provides for only one (base addressing). The remaining modes are provided by the assembler. The MIPS64 has two additional addressing modes for use in embedded systems optimizations.

The MIPS instructions in Chapter 4 had up to four fields: an opcode, two operand addresses, and one result address. Essentially three instruction formats are available: the I type (immediate), the R type (register), and the J type (jump).

R type instructions have a 6-bit opcode, a 5-bit source register, a 5-bit target register, a 5-bit shift amount, and a 6-bit function. I type instructions have a 6-bit operand, a 5-bit source register, a 5-bit target register or branch condition, and a 16-bit immediate branch displacement or address displacement. J type instructions have a 6-bit opcode and a 26-bit target address.

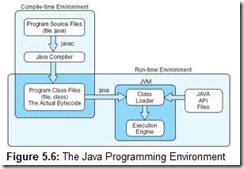
5.6.3 Java Virtual Machine

Java, a language that is becoming quite popular, is very interesting in that it is platform independent. This means that if you compile code on one architecture (say a Pentium) and you wish to run your program on a different architecture (say a Sun workstation), you can do so without modifying or even recompiling your code.

The Java compiler makes no assumptions about the underlying architecture of the machine on which the program will run, such as the number of registers, memory size, or I/O ports, when you first compile your code. After compilation, however, to execute your program, you will need a Java Virtual Machine (JVM) for the architecture on which your program will run. (A virtual machine is a software emulation of a real machine.) The JVM is essentially a “wrapper” that goes around the hardware architecture, and is very platform dependent. The JVM for a Pentium is different from the JVM for a Sun workstation, which is different from the JVM for a Macintosh, and so on. But once the JVM exists on a particular architecture, that JVM can execute any Java program compiled on any ISA platform. It is the JVM’s responsibility to load, check, find, and execute bytecodes at run time. The JVM, although virtual, is a nice example of a well-designed ISA.

The JVM for a particular architecture is written in that architecture’s native instruction set. It acts as an interpreter, taking Java bytecodes and interpreting them into explicit underlying machine instructions. Bytecodes are produced when a Java program is compiled. These bytecodes then become input for the JVM. The JVM can be compared to a giant switch (or case) statement, analyzing one bytecode instruction at a time. Each bytecode instruction causes a jump to a specific block of code, which implements the given bytecode instruction.

This differs significantly from other high-level languages with which you may be familiar. For example, when you compile a C++ program, the object code produced is for that particular architecture. (Compiling a C++ program results in an assembly language program that is translated to machine code.) If you want to run your C++ program on a different platform, you must recompile it for the target architecture. Compiled languages are translated into runnable files of the binary machine code by the compiler. Once this code has been generated, it can be run only on the target architecture. Compiled languages typically exhibit excellent performance and give very good access to the operating system. Examples of compiled languages include C, C++, Ada, FORTRAN, and COBOL.

Some languages, such as LISP, PhP, Perl, Python, Tcl, and most BASIC languages, are interpreted. The source must be reinterpreted each time the program is run. The trade-off for the platform independence of interpreted languages is slower performance-usually by a factor of 100 times. (We will have more to say on this topic in Chapter 8.)

Languages that are a bit of both (compiled and interpreted) exist as well. These are often called P-code languages. The source code written in these languages is compiled into an intermediate form, called P-code, and the P-code is then interpreted. P-code languages typically execute from 5 to 10 times more slowly than compiled languages. Python, Perl, and Java are actually P-code languages, even though they are typically referred to as interpreted languages.

Figure 5.6 presents an overview of the Java programming environment.

Perhaps more interesting than Java’s platform independence, particularly in relationship to the topics covered in this chapter, is the fact that Java’s bytecode is a stack-based language, partially composed of zero address instructions. Each instruction consists of a one-byte opcode followed by zero or more operands. The opcode itself indicates whether it is followed by operands and the form the operands (if any) take. Many of these instructions require zero operands.

Java uses two’s complement to represent signed integers but does not allow for unsigned integers. Characters are coded using 16-bit Unicode. Java has four registers, which provide access to five different main memory regions. All references to memory are based on offsets from these registers; pointers or absolute memory addresses are never used. Because the JVM is a stack machine, no general registers are provided. This lack of general registers is detrimental to performance, as more memory references are generated. We are trading performance for portability.

Let’s take a look at a short Java program and its corresponding bytecode. Example 5.2 shows a Java program that finds the maximum of two numbers.

Example 5.2:

Here is a Java program to find the maximum of two numbers.

public class Maximum {
 
  public static void main (String[] Args)
  { int X,Y,Z;
    X = Integer.parseInt(Args[0]);
    Y = Integer.parseInt(Args[1]);
    Z = Max(X,Y);
    System.out.println(Z);
  }
 
  public static int Max (int A, int B)
  { int C;
    if (A>B)C=A;
    else C=B;
    return C;
  }
}

After we compile this program (using javac), we can disassemble it to examine the bytecode, by issuing the following command:

javap -c Maximum

You should see the following:

Compiled from Maximum.java
public class Maximum extends java.lang.Object {
    public Maximum();
    public static void main(java.lang.String[]);
    public static int Max(int, int);
}
Method Maximum()
   0 aload_0
   1 invokespecial #1 <Method java.lang.Object()>
   4 return
Method void main(java.lang.String[])
   0 aload_0
   1 iconst_0
   2 aaload
   3 invokestatic #2 <Method int parseInt(java.lang.String)>
   6 istore_1
   7 aload_0
   8 iconst_1
   9 aaload
  10 invokestatic #2 <Method int parseInt(java.lang.String)>
  13 istore_2
  14 iload_1
  15 iload_2
  16 invokestatic #3 <Method int Max(int, int)>
  19 istore_3
  20 getstatic #4 <Field java.io.PrintStream out>
  23 iload_3
  24 invokevirtual #5 <Method void println(int)>
  27 return
Method int Max(int, int)
   0 iload_0
   1 iload_1
   2 if_icmple 10
   5 iload_0
   6 istore_2
   7 goto 12
  10 iload_1
  11 istore_2
  12 iload_2
  13 ireturn

Each line number represents an offset (or the number of bytes that an instruction is from the beginning of the current method). Notice that

Z = Max (X,Y);

gets compiled to the following bytecode:

14 iload_1
14 iload_1
15 iload_2
16 invokestatic #3 <Method int Max(int, int)>
19 istore_3

It should be very obvious that Java bytecode is stack-based. For example, the iadd instruction pops two integers from the stack, adds them, and then pushes the result back to the stack. There is no such thing as “add r0, r1, f2” or “add AC, X”. The iload_1 (integer load) instruction also uses the stack by pushing slot 1 onto the stack (slot 1 in main contains X, so X is pushed onto the stack). Y is pushed onto the stack by instruction 15. The invokestatic instruction actually performs the Max method call. When the method has finished, the istore_3 instruction pops the top element of the stack and stores it in Z.

We will explore the Java language and the JVM in more detail in Chapter 8.

Chapter Summary

The core elements of an instruction set architecture include the memory model (word size and how the address space is split), registers, data types, instruction formats, addressing, and instruction types. Even though most computers today have general purpose register sets and specify operands by combinations of memory and register locations, instructions vary in size, type, format, and the number of operands allowed. Instructions also have strict requirements for the locations of these operands. Operands can be located on the stack, in registers, in memory, or a combination of the three.

Many decisions must be made when ISAs are designed. Larger instruction sets mandate longer instructions, which means a longer fetch and decode time. Instructions having a fixed length are easier to decode but can waste space. Expanding opcodes represent a compromise between the need for large instruction sets and the desire to have short instructions. Perhaps the most interesting debate is that of little versus big endian byte ordering.

There are three choices for internal storage in the CPU: stacks, an accumulator, or general purpose registers. Each has its advantages and disadvantages, which must be considered in the context of the proposed architecture’s applications. The internal storage scheme has a direct impact on the instruction format, particularly the number of operands the instruction is allowed to reference. Stack architectures use zero operands, which fits well with RPN notation.

Instructions are classified into the following categories: data movement, arithmetic, Boolean, bit manipulation, I/O, transfer of control, and special purpose. Some ISAs have many instructions in each category, others have very few in each category, and many have a mix of each.

The advances in memory technology, resulting in larger memories, have prompted the need for alternative addressing modes. The various addressing modes introduced included immediate, direct, indirect, register, indexed, and stack. Having these different modes provides flexibility and convenience for the programmer without changing the fundamental operations of the CPU.

Instruction-level pipelining is one example of instruction-level parallelism. It is a common but complex technique that can speed up the fetch-decode-execute cycle. With pipelining we can overlap the execution of instructions, thus executing multiple instructions in parallel. However, we also saw that the amount of parallelism can be limited by conflicts in the pipeline. Whereas pipelining performs different stages of multiple instructions at the same time, superscalar architectures allow us to perform multiple operations at the same time. Superpipelining, a combination of superscalar and pipelining, in addition to VLIW, was also briefly introduced. There are many types of parallelism, but at the computer organization and architecture level, we are really concerned mainly with ILP.

Intel and MIPS have interesting ISAs, as we have seen in this chapter as well as in Chapter 4. However, the Java Virtual Machine is a unique ISA, because the ISA is built in software, thus allowing Java programs to run on any machine that supports the JVM. Chapter 8 covers the JVM in great detail.

Review of Essential Terms and Concepts

1. Explain the difference between register-to-register, register-to-memory, and memory-to-memory instructions.

2. Several design decisions exist with regard to instruction sets. Name four and explain.

3. What is an expanding opcode?

4. If a byte-addressable machine with 32-bit words stores the hex value 98765432, indicate how this value would be stored on a little endian machine and on a big endian machine. Why does “endian-ness” matter?

5. We can design stack architectures, accumulator architectures, or general-purpose register architectures. Explain the differences between these choices and give some situations where one might be better than another.

6. How do memory-memory, register-memory, and load-store architectures differ? How are they the same?

7. What are the pros and cons of fixed-length and variable-length instructions? Which is currently more popular?

8. How does an architecture based on zero operands ever get any data values from memory?

9. Which is likely to be longer (have more instructions): a program written for a zero-address architecture, a program written for a one-address architecture, or a program written for a two-address architecture? Why?

10. Why might stack architectures represent arithmetic expressions in reverse Polish notation?

11. Name the seven types of data instructions and explain each.

12. What is an address mode?

13. Give examples of immediate, direct, register, indirect, register indirect, and indexed addressing.

14. How does indexed addressing differ from based addressing?

15. Why do we need so many different addressing modes?

16. Explain the concept behind pipelining.

17. What is the theoretical speedup for a 4-stage pipeline with a 20ns clock cycle if it is processing 100 tasks?

18. What are the pipeline conflicts that can cause a slowdown in the pipeline?

19. What are the two types of ILP and how do they differ?

20. Explain superscalar, superpipelining, and VLIW architectures.

21. List several ways in which the Intel and MIPS ISAs differ. Name several ways in which they are the same.

22. Explain Java bytecodes.

23. Give an example of a current stack-based architecture and a current GPR-based architecture. How do they differ?

Exercises

1. Assume you have a machine that uses 32-bit integers and you are storing the hex value 1234 at address 0:

   1. Hints and Answers Show how this is stored on a big endian machine.

   2. Hints and Answers Show how this is stored on a little endian machine.

   3. If you wanted to increase the hex value to 123456, which byte assignment would be more efficient, big or little endian? Explain your answer.

2. Show how the following values would be stored by machines with 32-bit words, using little endian and then big endian format. Assume each value starts at address 10₁₆. Draw a diagram of memory for each, placing the appropriate values in the correct (and labeled) memory locations.

   1. 456789A1₁₆

   2. 0000058A₁₆

   3. 14148888₁₆

3. Hints and Answers The first two bytes of a 2M x 16 main memory have the following hex values:

   • Byte 0 is FE

   • Byte 1 is 01

   If these bytes hold a 16-bit two’s complement integer, what is its actual decimal value if:

   1. Hints and Answers memory is big endian?

   2. Hints and Answers memory is little endian?

4. What kinds of problems do you think endian-ness can cause if you wished to transfer data from a big endian machine to a little endian machine? Explain.

5. Hints and Answers The Population Studies Institute monitors the population of the United States. In 2000, this institute wrote a program to create files of the numbers representing populations of the various states, as well as the total population of the U.S. This program, which runs on a Motorola processor, projects the population based on various rules, such as the average number of births and deaths per year. The institute runs the program and then ships the output files to state agencies so the data values can be used as input into various applications. However, one Pennsylvania agency, running all Intel machines, encountered difficulties, as indicated by the following problem. When the 32-bit unsigned integer 1D2F37E8₁₆ (representing the overall U.S. population prediction for 2003) is used as input, and the agency’s program simply outputs this input value, the U.S. population forecast for 2003 is far too large. Can you help this Pennsylvania agency by explaining what might be going wrong?

6. There are reasons for machine designers to want all instructions to be the same length. Why is this not a good idea on a stack machine?

7. Hints and Answers A computer has 32-bit instructions and 12-bit addresses. Suppose there are 250 2-address instructions. How many 1-address instructions can be formulated? Explain your answer.

8. Convert the following expressions from infix to reverse Polish (postfix) notation.

   1. Hints and Answers X x Y + W x Z + V x U

   2. W x X + W x (U x V + Z)

   3. (W x (X + Y x (U x V)))/(U x (X + Y))

9. Convert the following expressions from reverse Polish notation to infix notation.

   1. W X Y Z – + x

   2. U V W X Y Z + x + x +

   3. X Y Z + V W – x Z + +

10. 1. Write the following expression in postfix (reverse Polish) notation. Remember the rules of precedence for arithmetic operators!

       

    2. Write a program to evaluate the above arithmetic statement using a stack organized computer with zero-address instructions (so only pop and push can access memory).

11. 1. In a computer instruction format, the instruction length is 11 bits and the size of an address field is 4 bits. Is it possible to have

       5 2-address instructions

       45 1-address instructions

       32 0-address instructions

       using the format? Justify your answer.

    2. Assume that a computer architect has already designed 6 two-address and 24 zero-address instructions using the instruction format given in Problem 11. What is the maximum number of one-address instructions that can be added to the instruction set?

12. What is the difference between using direct and indirect addressing? Give an example.

13. Hints and Answers Suppose we have the instruction Load 1000. Given that memory and register R1 contain the values below:

    

    Assuming R1 is implied in the indexed addressing mode, determine the actual value loaded into the accumulator and fill in the table below:

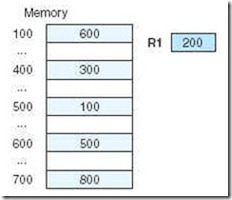
14. Suppose we have the instruction Load 500. Given that memory and register R1 contain the values below:

    

    Assuming R1 is implied in the indexed addressing mode, determine the actual value loaded into the accumulator and fill in the table below:

15. A nonpipelined system takes 200ns to process a task. The same task can be processed in a 5-segment pipeline with a clock cycle of 40ns. Determine the speedup ratio of the pipeline for 200 tasks. What is the maximum speedup that could be achieved with the pipeline unit over the nonpipelined unit?

16. A nonpipeline system takes 100ns to process a task. The same task can be processed in a 5-stage pipeline with a clock cycle of 20ns. Determine the speedup ratio of the pipeline for 100 tasks. What is the theoretical speedup that could be achieved with the pipeline system over a nonpipelined system?

17. Write code to implement the expression A = (B + C) x (D + E) on 3-, 2-, 1-, and 0-address machines. In accordance with programming language practice, computing the expression should not change the values of its operands.

18. Hints and Answers A digital computer has a memory unit with 24 bits per word. The instruction set consists of 150 different operations. All instructions have an operation code part (opcode) and an address part (allowing for only one address). Each instruction is stored in one word of memory.

    1. Hints and Answers How many bits are needed for the opcode?

    2. Hints and Answers How many bits are left for the address part of the instruction?

    3. Hints and Answers What is the maximum allowable size for memory?

    4. Hints and Answers What is the largest unsigned binary number that can be accommodated in one word of memory?

19. The memory unit of a computer has 256K words of 32 bits each. The computer has an instruction format with 4 fields: an opcode field; a mode field to specify 1 of 7 addressing modes; a register address field to specify 1 of 60 registers; and a memory address field. Assume an instruction is 32 bits long. Answer the following:

    1. How large must the mode field be?

    2. How large must the register field be?

    3. How large must the address field be?

    4. How large is the opcode field?

20. Suppose an instruction takes four cycles to execute in a nonpipelined CPU: one cycle to fetch the instruction, one cycle to decode the instruction, one cycle to perform the ALU operation, and one cycle to store the result. In a CPU with a 4-stage pipeline, that instruction still takes four cycles to execute, so how can we say the pipeline speeds up the execution of the program?

21. * Pick an architecture (other than those covered in this chapter). Do research to find out how your architecture approaches the concepts introduced in this chapter, as was done for Intel, MIPS, and Java.

True or False.

1. Most computers typically fall into one of three types of CPU organization: (1) general register organization; (2) single accumulator organization; or (3) stack organization.

2. The advantage of zero-address instruction computers is that they have short programs; the disadvantage is that the instructions require many bits, making them very long.