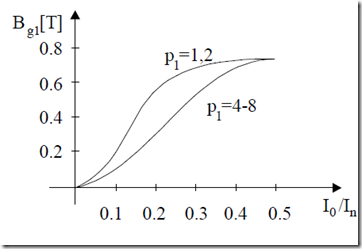
The dependence of airgap flux density fundamental Bg1 on stator mmf fundamental amplitude F1m for zero rotor currents is called the magnetization curve.
For mild levels of magnetic saturation, usually in general, purpose induction motors, the stator mmf fundamental produces a sinusoidal distribution of the flux density in the airgap (slotting is neglected). As shown later in this chapter by balancing the magnetic saturation of teeth and back cores, rather sinusoidal airgap flux density is maintained, even for very heavy saturation levels. The basic magnetization curve (F1m(Bg1) or I0(Bg1) or Io/In versus Bg1) is very important when designing an induction motor and notably influences the power factor and the core loss. Notice that I0 and In are no load and full load stator phase currents and F1m0 is
F1m0 = 3 2W Kπp11 w1 0I (5.14)
The no load (zero rotor current) design airgap flux density is Bg1 = 0.6 – 0.8T for 50 (60) Hz induction motors and goes down to 0.4 to 0.6 T for (400 to 1000) Hz high speed induction motors, to keep core loss within limits. On the other hand, for 50 (60) Hz motors, I0/In (no-load current/rated current) decreases with motor power from 0.5 to 0.8 (in subkW power range) to 0.2 to 0.3 in the high power range, but it increases with the number of pole pairs.
Figure 5.7 Typical magnetization curves
For low airgap flux densities, the no-load current tends to be smaller. A typical magnetization curve is shown in Figure 5.7 for motors in the kW power range at 50 (60) Hz.
Now that we do have a general impression on the magnetising (mag.) curve, let us present a few analytical methods to calculate it.
5.4.1 The magnetization curve via the basic magnetic circuit
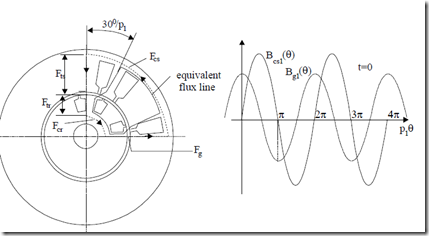
We shall examine first the flux lines corresponding to maximum flux density in the airgap and assume a sinusoidal variation of the latter along the pole pitch (Figure 5.8a,b).
Bg1(θe,t)= Bg1m cos p( 1θ−ω1t ; ) θ =e p1θ (5.15)
For t = 0 Bg(θ,0)= Bg1m cosp1θ (5.16)
The stator (rotor) back iron flux density Bcs,r is
θ
Bcs,r =
θ θ⋅ D (5.17)
where hcs,r is the back core height in the stator (rotor). For the flux line in Figure 5.8a (θ = 0 to π/p1),
Bcs1(θ,t)= 12 π2 hτcs ⋅Bg1m sin p( 1θ−ω1t ; ) τ = 2πpD1 (5.18)
Figure 5.8 Flux path a.) and flux density types b.): ideal distribution in the airgap and stator core
Due to mmf and airgap flux density sinusoidal distribution along motor periphery, it is sufficient to analyse the mmf iron and airgap components Fts, Ftr in teeth, Fg in the airgap, and Fcs, Fcr in the back cores. The total mmf is represented by F1m (peak values).
2F1m = 2Fg + 2Fts + 2Ftr + Fcs + Fcr (5.19)
Equation (5.19) reflects the application of the magnetic circuit (Ampere’s) law along the flux line in Figure 5.8a.
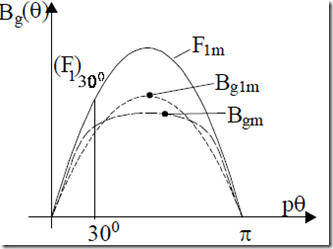
In industry, to account for the flattening of the airgap flux density due to teeth saturation, Bg1m is replaced by the actual (designed) maximum flattened flux density Bgm, at an angle θ = 30°/p1, which makes the length of the flux lines in the back core 2/3 of their maximum length.
![clip_image001[4]](http://machineryequipmentonline.com/electric-equipment/wp-content/uploads/2017/03/clip_image0014.gif "clip_image001[4]"){kind=small}
Then finally the calculated I1m is multiplied by 2/ 3 (1/cos30°) to find the maximum mmf fundamental.
At θer = p1θ = 30°, it is supposed that the flattened and sinusoidal flux density are equal to each other (Figure 5.9).
We have to again write Ampere’s law for this case (interior flux line in Figure 5.8a).
2( )F1 300 = 2F Bg ( gm )+ 2Fts + 2Ftr + Fcs + Fcr (5.20) and finally, 2F1m = 2cos( )F1303000 (5.21)
For the sake of generality we will use (5.20) – (5.21), remembering that the length of average flux line in the back cores is 2/3 of its maximum.
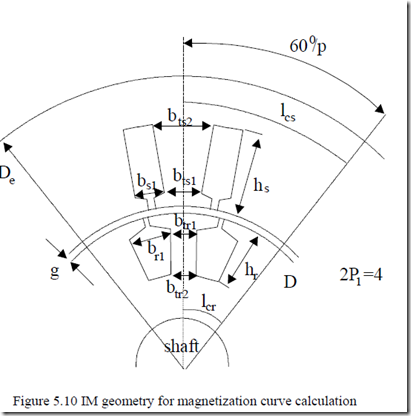
Let us proceed directly with a numerical example by considering an induction motor with the geometry in Figure 5.10.
2p1 = 4; D = 0.1m; De = 0.176m; hs = 0.025m; Ns = 24;
Nr =18; br1 =1.2btr1; bs1 =1.4bts1; g = 0.5⋅10-3m; (5.22) hr = 0.018m; Dshaft = 0.035m; Bgm
Figure 5.10 IM geometry for magnetization curve calculation