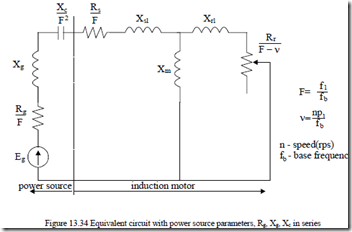
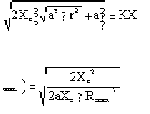SUBSYNCHRONOUS RESONANCE (SSR)

Subsynchronous series resonance may occur when the induction motors are fed from a power source that shows a series capacitance (Figure 13.34). It may lead to severe oscillations in speed, torque, and current. It appears, in general, during machine starting or after a power supply fault.

f_b is the base frequency, f₁ is the current frequency, n is the rotor speed. The reactances are written at base frequency.

It is self evident that the space phasor model may be used directly to solve this problem completely, provided a new variable (capacitor voltage V_c) is introduced.

^dVc = ¹ is (13.137) dt C

The total solution contains a forced solution and a free solution. The complete mathematical model is complex when magnetic saturation is considered. It simplifies greatly if the magnetization reactance X_m is considered constant (though at a saturated value). In contrast to the induction capacitorexcited generator, the free solution here produces conditions that lead to machine heavy saturation.

In such conditions we may treat separately the resonance conditions for the free solution.

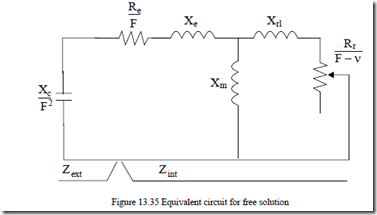
To do so we lump the power source impedance R_g, X_g into stator parameters to get  R_e = R_s + R ; X_{g e} = X_g + X_sl (13.138) and eliminate the generator (power source) emf E_g (Figure 13.35).

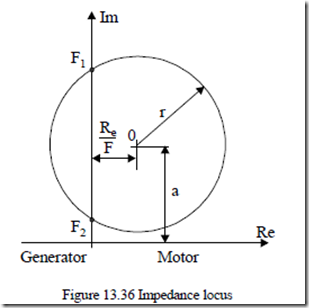
To simplify the analysis, let us use a graphical solution. The internal impedance locus is, as known, a circle with the center 0 at 0^{ Re} ,a^ . [28]

 F 

a ≈ Xe + 2(XXe +e2Xm ) (13.139)

and the radius r

r ≈ 2(_X^Xe ₊^e2_Xm ₎ (13.140)

On the other hand, the external (the capacitor, in fact) impedance is represented by the imaginary axis (Figure 13.36). The intersection of the circle with the imaginary axis, for a given capacitor, takes place in two points F₁ and F₂ which correspond to reference conditions. F₁ corresponds to the lower slip and is the usual self excitation point of induction generators.

The p.u. values of frequencies F₁ and F₂, for a given series capacitor X_c and resistor, R_e, reactance X_e, are

F₁ ≈ Xe + Xm

X_c

F2 ≈ Xe + XXX Xmc_m+ X_rl rl (13.141)

Alternatively, for a given resonance frequency and capacitor, we may obtain the resistance R_e to cause subsynchronous resonance. With F = F₁ given, we may use the impedance locus to obtain R_e.

XF 2c = a + r2 − RF1e 2 (13.142)

1

Also, from the internal impedance at R_e(Z_int) = 0 equal to X_c/F₁², the value of speed (slip: F–ν) may be obtained.

 Xc 

slip = F −ν ≈ ± Rr ^Xm −Xe − F12  (13.143)

₁ (Xm + Xrl ) XF1c −Xe (Xm + Xrl )−X Xm rl 

 2

In general, we may use Equation (13.143) with both ± to calculate the frequencies for which resonance occurs.

F a⁴ ( ² − +r² ) F R² ( _e² −2aX_c )+X_c² = 0 (13.144)

The maximum value of R_e, which still produces resonance, is obtained when the discriminant of (13.144) becomes zero.

R_emax = _c (13.145)

The corresponding frequency,

F R( (13.146)

This way the range of possible source impedance that may produce subsynchronous resonance (SSR) has been defined.

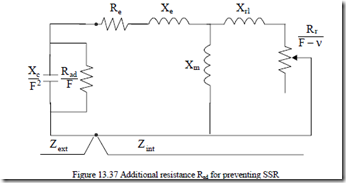
Preventing SSR may be done either by increasing R_e above R_emax (which means notable losses) or by connecting a resistor R_ad in parallel with the capacitor (Figure 13.37), which means less losses.

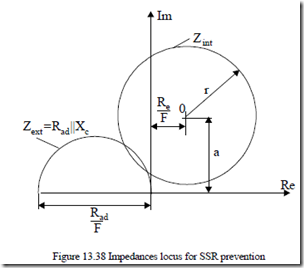
A graphical solution is at hand as Z_int locus is already known (the circle). The impedance locus of the R_ad||X_c circuit is a half circle with the diameter R_ad/F and the center along the horizontal negative axis (Figure 13.38).

The SSR is eliminated if the two circles, at same frequency, do not intersect each other. Analytically, it is possible to solve the equation:

Z_ext + Z_int = 0 (13.146’) again, with R_ad||X_c as Z_ext.

A 6^th order polynomial equation is obtained. The situation with a double real root and 4 complex roots corresponds to the two circles being tangent. Only one SSR frequency occurs. This case defines the critical value of R_ad for SSR. In general, R_ad (critical) increases with X_c and so does the corresponding SSR frequency. [27, 28]

Using a series capacitor for starting medium power IMs to reduce temporary supply voltage sags and starting time is a typical situation when the prevention SSR is necessary.