SIMPLIFIED LEAKAGE SATURATION CORRECTIONS

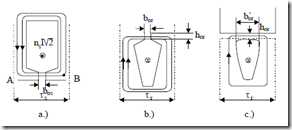
Further on, for large values of currents (large slips), the stator (rotor) tooth tops tend to be saturated by the slot leakage flux (Figure 6.14).

Neglecting the magnetic saturation along the tooth height, we may consider that only the tooth top saturates due to the slot neck leakage flux produced by the entire slot mmf.

Figure 6.14 Slot neck leakage flux

a.) stator semiclosed slot b.) rotor semiclosed slot c.) rotor closed slot

A simple way to account for this leakage saturation that is used widely in industry consists of increasing the slot opening b_os,r by the tooth top length t_t divided by the relative iron permeability µ_rel within it.

tt = τs,r − bos,r

b’ = bos,r + µtrelt (6.73) os,r

For the closed slot (Figure 6.14), we may use directly (6.31). To calculate µ_rel, we apply the Ampere’s and flux laws.

Bt = µ0H0

(6.74) n I 2s = t Ht t + H b0 os,r

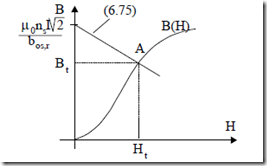
µ₀n I 2_s = µ₀t H_{t t} + B b_{t os,r}; B₀ = B_t (6.75)

We have to add the lamination magnetization curve, B_t(H_t), to (6.75) and intersect them (Figure 6.15) to find B_t and H_t, and, finally,

µrel = µB0Ht t (6.76)

H₀–magnetic field in the slot neck.

Given the slot mmf n I 2_s (the current, in fact), we may calculate iteratively µ_rel (6.76) and, from (6.73), the corrected b_os,r (b’_os,r) then to be used in geometrical slot permeance calculations.

As expected, for open slots, the slot leakage saturation is negligible. Simple as it may seem, a second iteration process is required to find the current, as, in general, a voltage type supply is used to feed the IM.

It may be inferred that both differential and skewing leakage are influenced by saturation, in the sense of reducing them. For the former, we already introduced the partial teeth saturation factor K_st = K_sd to account for it (6.14). For the latter, in (6.48), we have assumed that the level of saturation is implicitly accounted for L_1m (that is, it is produced by the magnetization current in the machine). In reality, for large rotor currents, the skewing rotor mmf field, dependent on rotor current and axial position along stack, is quite different from that of the main flux path, at standstill.

However, to keep the formulas simple, Equation (6.73) has become rather standard for design purposes.

Zig-zag flux path tends also to be saturated at high currents. Notice that the zig-zag flux path occupies the teeth tops (Figure 6.10b). This aspect is conventionally neglected as the zig-zag leakage inductance tends to be a small part of total leakage inductance.

So far, we considered the leakage saturation through simple approximate correction factors, and treated skin effects only for rectangular coils. In Chapter 9 we will present comprehensive methods to treat these phenomena for slots of general shapes. Such slot shapes may be the result of design optimization methods based on various cost (objective) functions such as high starting torque, low starting current, large peak torque, etc.

. REDUCING THE ROTOR TO STATOR

The main flux paths embrace both the stator and rotor slots passing through an airgap. So the two emfs per phase E1 (Chapter 5.10) and E2 are

E1 = − πj 2W K K1 q1 y1 1f Φ1; Φ =1 π2 Bg1τLe (6.77)

E2 = − πj 2W K2 q2Ky2K f Sc2 1 Φ1 (6.77)

We have used phasors in (6.77) and (6.78) as E1, E2 are sinusoidal in time (only the fundamental is accounted for).

Also in (6.78), E2 is already calculated as “seen from the stator side,” in terms of frequency because only in this case Φ1 is the same in both stator and rotor phases. In reality the flux in the rotor varies at Sf1 frequency, while in the stator at f1 frequency. The amplitude is the same and, with respect to each other, they are at stall.

Now we may proceed as for transformers by dividing the two equations to obtain

EE12 = W KW K21 w1w2 = Ke = V ‘Vrr (6.79)

Ke is the voltage reduction factor to stator.

Eventually the actual and the stator reduced rotor mmfs should be identical:

m1 2πKpw1 r1 I ‘W1 = m2 2πKpw2 r1 I W2 (6.80)

From (6.80) we find the current reduction factor Ki.

Ki = I ‘Irr = m Km K21 w2w1WW12 (6.81)

For the rotor resistance and reactance equivalence, we have to conserve the conductor losses and leakage field energy.

m R ‘I ‘1 r r 2 = m R I2 r r2 (6.82) m1 L ‘2rl I ‘r 2 = m2 L2rl Ir2 (6.83)

So, R ‘r = Rr mm12 K1i2 ; L ‘rl = Lrl mm12 K1i2 (6.84)

For cage rotors, we may still use (6.81) and (6.84) but with m2 = Nr, W2 = ½, and Kw2 = Kskew (skewing factor); that is, each bar (slot) represents a phase.

R ‘r = Rbe 12Kw12W212

N Kr skew

(6.85)

Lbe’= Lbe 12Kw12W212

(6.86)

N Kr skew

Notice that only the slot and ring leakage inductances in (6.86) have to be reduced to the stator in Lrl (6.81).

L ‘rl = (Ldlr + Lzlr + Lskew,r )+ Lbe’ (6.87)

Example 6.4. Let us consider an IM with q = 3, p1 = 2, (Ns = 36slots), W1 = 300 turns/phase, Kw1 = 0.965, Nr = 30 slots, one stator slot pitch rotor skewing (c/τ = 1/3q) (Kskew = 0.9954), and the rotor bar (slot) and end ring cross sections are rectangular (hr/b1 = 2/1), hor = 1.5⋅10-3m, and bor = 1.5⋅10-3m, Le = 0.12m. Let us find the bar ring resistance and leakage inductance reduced to the stator.

Solution

From Example 6.3, we take Dir = 0.15 m, Ai = a × b = 481 mm2 for the end ring. We may assume a/b = ½ and, thus, a = 15.51⋅10-3 m and b = 31 mm. The bar cross-section in example 6.3 is Ab = 166 mm2.

b1 = (h / brAb 1) = 1662 ≈ 9.1mm; hr =18.2mm (6.88)

From example 6.3 we already know the equivalent bar resistance (6.70) Rbe = 3.804⋅10-5 Ω.

Also from (6.19), the rounded geometrical slot permenace λr is,

λ = λ ≈ + = (6.89)

From (6.46), the end ring segment geometrical permeance λei may be found.

λei = 4N L sinr 2.3e Dir2 πNPr1 lg a4.7+D2bi =

(6.90)

with Li = π Di/Nr = π ⋅150/30 = 15.7⋅10-3m.

Now from (6.39) and (6.40), the bar and end ring leakage inductances are

LLlib == µµ00llibλλeibar==1.1.256 10256 10⋅ ⋅ −6−6⋅0.⋅0.015714⋅1.⋅1.66964= 0.=292 100.3872 10⋅ −⋅6H−8H (6.91)

The equivalent bar leakage inductance Lbe (6.52) is written:

Lbe = Lb + 2Lei = 0.292 10⋅ −6 + 2 0.⋅ 3872 10⋅ −8 = 0.2997 10⋅ −6 H (6.92)

From (6.85) and (6.86) and we may now obtain the rotor slot (bar) and end ring equivalent resistance and leakage inductance reduced to the stator,

R ‘r Rbe N Kr skew 30⋅0.99 =1.28Ω (6.93)

Lbe’= Lbe = 0.2997 10⋅ −6 ⋅0.36 10⋅ −5 =1.008 10⋅ −2 H (6.94)

N Kr skew

As a bonus, knowing from Example 6.3 that the magnetization inductance L1m = 0.1711H, we may calculate the rotor skewing leakage inductance (from 6.48), which is already reduced to the stator because it is a fraction of L1m,

Lskew,r = (1−Kskew2 )⋅L1m = (1−0.99542 )⋅0.1711=1.57 10⋅ −3H (6.95)

In this particular case the skewing leakage is more than 6 times smaller than the slot (bar) and end ring leakage inductance. Notice also that Lbe′/L1m = 0.059, a rather practical value.