Other Binary Operations
One useful area of digital activity is related to filtering, and its activity can be described by similar algebra. The technique uses a shift register whose output is fed back and combined with the incoming logic signal. Feedback is usually arranged to come from earlier stages as well as the final output stage. The arrangement can be considered as a form of binary division. For certain combinations of feedback the output of the shift register can be considered as a statistically dependable source of random numbers. In the simplest form the random output can be formed in the analogue domain by the simple addition of a suitable low-pass filter. Such a random noise generator has the useful property that the noise waveform is repeated, which allows the results of stimulating a system with such a signal to be averaged.
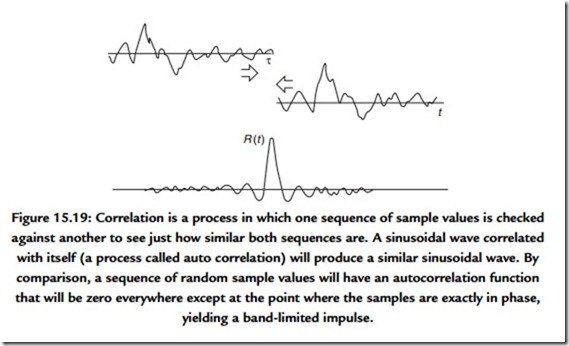
When a sequence of samples with a nominally random distribution of values is correlated with itself, the result is identical to a band-limited impulse (Figure 15.19). If such a random signal is used to stimulate a system (this could be an artificial reverberation device, an equalizer, or a loudspeaker under test) and the resulting output is correlated with the input sequence, the result will be the impulse response of the system under test.
The virtue of using a repeatable excitation noise is that measurements can be made in the presence of other random background noise or interference, and if further accuracy is required, the measurement is simply repeated and the results averaged. True random
background noise will average out, leaving a “cleaner” sequence of sample values that describe the impulse response. This is the basis behind practical measurement systems.
Shift registers combined with feedback are also used in error detecting and correction systems.