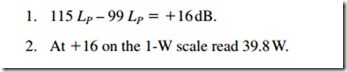Combining Voltage
To combine voltages, use the following equation:
where ET is the total sound pressure, current, or voltage; E1 is the sound pressure, current, or voltage of the first signal; E2 is the sound pressure, current, or voltage of the second signal; a1 is the phase angle of signal one; and a2 is the phase angle of signal two.
Using the Log Charts
The 10 Log x Chart
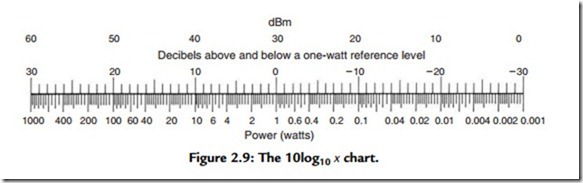
There are two scales on the top of the 10 log10 x chart in Figure 2.9. One is in dB above and below a 1-W reference level and the other is in dBm (reference 0.001 W). Power ratios may be read directly from the 1-W dB scale.
Example
How many decibels is a 25:1 power ratio?
1. Look up 25 on the power–watts scale.
2. Read 14 dB directly above the 25.
Example
We have a 100 W amplifier but plan to use a 12-dB margin for “head room.” How many watts will our program level be?
1. Above 100 W find +50 dBm.
2. Subtract 12 dB from 50 dBm to obtain +38 dBm. Just below +38 dBm find approximately 6 W.
Example
A 100-W amplifier has 64 dB of gain. What input level in dBm will drive it to full power?
1. Above 100 W read +50 dBm.
2. +50 dBm – 64-dB gain = -14 dBm.
Example
A loudspeaker has a sensitivity of LP = 99 dB at 4 ft with a 1-W input. How many watts are needed to have an LP of 115 at 4 ft?
The 20 Log x Chart
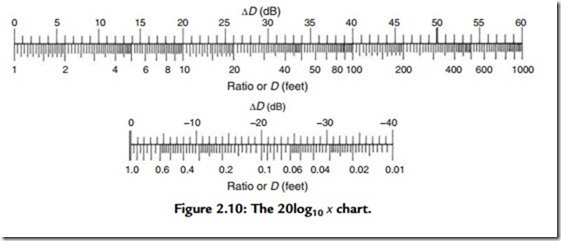
Refer to the chart in Figure 2.10. A 2:1 voltage, distance, or sound pressure change is found by locating 2 on the ratio or D scale and looking directly above to 6 dB.
Example
A loudspeaker has a sensitivity of LP = 99 dB at 4 ft with 1 W of input power. What will the level be at 100 ft?
1. Find the relative dB for 4 ft (relative dB = 12 dB).
2. Find the relative dB for 100 ft (relative dB = 40 dB).
3. Calculate the absolute dB (40 dB – 12 dB = 28 dB).
4. LP = 99 dB – 28 dB = 71 dB.
Example
If we raise the voltage from 2 to 10 V, how many decibels would we increase the power?
1. Find the relative dB for a ratio of 2 (relative dB = 6 dB).
2. Find the relative dB for a ratio of 10 (relative dB = 20 dB).
3. Absolute dB change = 20 dB – 6 dB = 14 dB.
4. Because a dB is a dB, the power also changed by 14 dB.