Why Does the Rotor Rotate ?
The reason why the rotor of an induction motor is set into rotation is as follow:
When the 3-phase stator windings, are fed by a 3-phase supply then, as seen from above, a magnetic flux of constant magnitude, but rotating at synchronous speed, is set up. The flux passes through the air-gap, sweeps past the rotor surface and so cuts the rotor conductors which, as yet, are stationary. Due to the relative speed between the rotating flux and the stationary conductors, an e.m.f. is induced in the latter, according to Faraday’s laws of electro-magnetic induction. The frequency of the induced e.m.f. is the same as the supply frequency. Its magnitude is proportional to
the relative velocity between the flux and the conductors and its direction is given by Fleming’s Right-hand rule. Since Windings of induction electric motor the rotor bars or conductors form a closed circuit, rotor current is produced whose direction, as given by Lenz’s law, is such as to oppose the very cause producing it. In this case, the cause which produces the rotor current is the relative velocity between the rotating flux of the stator and the stationary rotor conductors. Hence, to reduce the relative speed, the rotor starts running in the same direction as that of the flux and tries to catch up with the rotating flux.
The setting up of the torque for rotating the rotor is explained below :
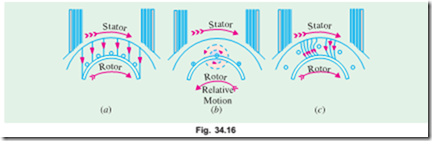
In Fig 34.16 (a) is shown the stator field which is assumed to be rotating clockwise. The relative motion of the rotor with respect to the stator is anticlockwise. By applying Right-hand rule, the direction of the induced e.m.f. in the rotor is found to be outwards. Hence, the direction of the flux due to rotor current alone, is as shown in Fig. 34.16 (b). Now, by applying the Left-hand rule, or by the effect of combined field [Fig. 34.16(c)] it is clear that the rotor conductors experience a force tending to rotate them in clockwise direction. Hence, the rotor is set into rotation in the same direction as that of the stator flux (or field).
Slip
In practice, the rotor never succeeds in ‘catching up’ with the stator field. If it really did so, then there would be no relative speed between the two, hence no rotor e.m.f., no rotor current and so no torque to maintain rotation. That is why the rotor runs at a speed which is always less than the speed of the stator field. The difference in speeds depends upon the load on the motor.*
The difference between the synchronous speed Ns and the actual speed N of the rotor is known as slip. Though it may be expressed in so many revolutions/second, yet it is usual to express it as a percentage of the synchronous speed. Actually, the term ‘slip’ is descriptive of the way in which the rotor ‘slips back’ from synchronism.
Obviously, rotor (or motor) speed is N = Ns (1 – s).
It may be kept in mind that revolving flux is rotating synchronously, relative to the stator (i.e. stationary space) but at slip speed relative to the rotor.
Frequency of Rotor Current
When the rotor is stationary, the frequency of rotor current is the same as the supply frequency. But when the rotor starts revolving, then the frequency depends upon the relative speed or on slip- speed. Let at any slip-speed, the frequency of the rotor current be f ¢. Then
phases of rotor winding, give rise to rotor magnetic fields. These individual rotor magnetic fields produce a combined rotating magnetic field, whose speed relative to rotor is
However, the rotor itself is running at speed N with respect to space. Hence, speed of rotor field in space = speed of rotor magnetic field relative to rotor + speed of rotor relative to space
It means that no matter what the value of slip, rotor currents and stator currents each produce a sinusoidally distributed magnetic field of constant magnitude and constant space speed of Ns. In other words, both the rotor and stator fields rotate synchronously, which means that they are stationary with respect to each other. These two synchronously rotating magnetic fields, in fact, superimpose on each other and give rise to the actually existing rotating field, which corresponds to the magnetising current of the stator winding.
Example 34.1. A slip-ring induction motor runs at 290 r.p.m. at full load, when connected to 50-Hz supply. Determine the number of poles and slip.
(Utilisation of Electric Power AMIE Sec. B 1991)
Related posts:
Incoming search terms:
- Why does the rotor rotate
- why does rotor rotate
- why rotor rotates
- why does rotor rotates
- Why does The rotor rotate?
- why rotor rotate
- why does rotor rotate in induction motor
- why does rotor rotates in induction motor
- how does rotor rotate
- why does the rotor of induction motor rotate
- why does rotor rotate?
- why does the rotor rotates
- How does rotor rotates
- induction motor rotation
- how does the rotor of an induction motor rotate
- howcthe rotor rotates
- how rotor rotates in induction motor
- why does the rotor of an induction motor rotate
- how rotating field produces torque
- 3 phase motor rotation right hand rule
- Why does the
- how the rotor of an induction motor rotates
- how does the rotor rotate in induction machine
- why tge rotor of induction machine has rotating flux
- which electric motor has it rotor and stator rotating simultaneously
- the direction of rotation of the fielin a 3 phase IM depends upon
- how a rotating magnetic field make an roter of an induction moter to roter
- explain how to rotating magnetic field makes to roter of an induction moter to roter
- rotor in induction motor runs in which direction
- explain how does the rotor of induction motor rotate?
- why does the rotar rotate
- why rotor is rotate
- why rotor rotes
- why does rotar rotates
- what does the rotor rotate
- how does the rotor rotates of an three phase induction motor
- the direction of rotation of rotor with respect to stator field is given by which rule
- why does rotar rotate
- how a rotor rotates
- why induction motor rotate anticlockwise
- rotor rotatng direction lenzs law
- www why a three phase induction motor rotates
- how to rotates the induction rotor
- How to rotet roter in im
- determine the motor rotor rotation law
- electric rotar
- how does roter is rotate
- how does roter roatet
- how does the rotor of a induction motor rotate
- how does the rotor and stator field superimposing