IDEAL NO-LOAD OPERATION

The ideal no-load operation mode corresponds to zero rotor current. From (7.11), for I_r0 = 0 we obtain

S₀E₂ − V_R = 0; S₀ ^{= V}_E^R₂ (7.17)

The slip S₀ for ideal no-load depends on the value and phase of the rotor applied voltage V_R. For V_R in phase with E₂: S₀ > 0 and, with them in opposite phase, S₀ < 0.

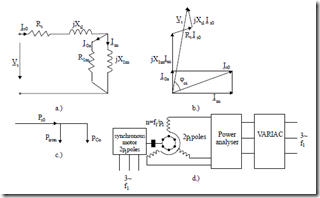
The conventional ideal no – load-synchronism, for the short-circuited rotor (V_R = 0) corresponds to S₀ = 0, n₀ = f₁/p₁. If the rotor windings (in a wound rotor) are supplied with a forward voltage sequence of adequate frequency f₂ = Sf₁ (f₁ > 0, f₂ > 0), subsynchronous operation (motoring and generating) may be obtained. If the rotor voltage sequence is changed, f₂ = sf₁ < 0 (f₁ > 0), supersynchronous operation may be obtained. This is the case of the doubly fed induction machine. For the time being we will deal, however, with the conventional ideal no-load (conventional synchronism) for which S₀ = 0. The equivalent circuit degenerates into the one in Figure 7.2a (rotor circuit is open).

Building the phasor diagram (Figure 7.2b) starts with I_m, continues with jX_1mI_m, then I_0a

Ioa = jXR1m1mIm (7.18)

and I_s0 = I_oa + I_m (7.19)

Finally, the stator phase voltage V_s (Figure 7.2b) is

Vs = jX1m Im + Rs Is0 + jXslIs0 (7.20)

The input (active) power P_s0 is dissipated into electromagnetic loss, fundamental and harmonics stator core losses, and stator windings and space harmonics caused rotor core and cage losses. The driving motor covers the mechanical losses and whatever losses would occur in the rotor core and squirrel cage due to space harmonics fields and hysteresis.

Figure 7.2 Ideal no-load operation (V_R = 0):

a.) equivalent circuit b.) phasor diagram c.) power balance d.) test rig

For the time being, when doing the measurements, we will consider only stator core and winding losses.



Ps0 ≈ 3R1m 0aI ² + 3R Is s02 = ^_3R1m X1mX2 1+mR2 1m2 + 3Rs Is02 = (7.21)

= piron + 3R Is s02

From d.c. measurements, we may determine the stator resistance R_s. Then, from (7.21), with P_s0, I_s0 measured with a power analyzer, we may calculate the iron losses p_iron for given stator voltage V_s and frequency f₁.

We may repeat the testing for variable f₁ and V₁ (or variable V₁/f₁) to determine the core loss dependence on frequency and voltage. The input reactive power is

Qs0 = 3X1m X1mR2 1+mR2 1m2 + 3Xsl Is02 (7.22)

From (7.21)-(7.22), with R_s known, Q_s0, I_s0, P_s0 measured, we may calculate only two out of the three unknowns (parameters): X_1m, R_1m, X_sl.

We know that R_1m >> X_1m >> X_sl. However, X_sl may be taken by the design value, or the value measured with the rotor out or half the stall rotor (S = 1) reactance X_sc, as shown later in this chapter.

Consequently, X_1m and R_1m may be found with good precision from the ideal no-load test (Figure 7.2d). Unfortunately, a synchronous motor with the same number of poles is needed to provide driving at synchronism. This is why the no-load motoring operation mode has become standard for industrial use, while the ideal no-load test is mainly used for prototyping.

Example 7.1 Ideal no-load parameters

An induction motor driven at synchronism (n = n₁ = 1800rpm, f₁ = 60Hz, p₁ = 2) is fed at rated voltage V₁ = 240 V (phase RMS) and draws a phase current I_s0 = 3 A, the power analyzer measures P_s0 = 36 W, Q_s0 = 700 VAR, the stator resistance R_s = 0.1 Ω, X_sl = 0.3 Ω. Let us calculate the core loss p_iron, X_1m, R_1m.

Solution

From (7.21), the core loss p_iron is

p_iron = P_s0 −3R I_{s s0}² = 36 −3 0.1 3⋅ ⋅ ² = 33.3W (7.23)

Now, from (7.21) and (7.22), we get

XR1m12m+X1Rm12m2 = Ps0 −3I3s0R I2s s02 = 36 −3 33 0.1 3⋅⋅ 2 ⋅ 2 = 3327.3 =1.233Ω (7.24)

XR1m 2 +XR1m1m2 = Qs0 −3I3s0X I2sl s02 = 700−3 33 0.3 3⋅⋅ 2 ⋅ 2 = 25.626Ω (7.25)

Dividing (7.25) by (7.26) we get

R1m = 25.626 = 20.78 (7.26)

X_1m 1.233

From (7.25),

X1m2 = 25.626; (20.X781m)2 +1 = 25.626 ⇒ X1m = 25.685 (7.27)



 XR11mm  +1

R_1m is calculated from (7.26),

R_1m = X_1m ⋅20.78 = 25.626 20⋅ .78 = 533.74Ω (7.28)

By doing experiments for various frequencies f₁ (and V_s/f₁ ratios), the slight dependence of R_1m on frequency f1 and on the magnetization current I_m may be proved.

As a bonus, the power factor cosϕ_oi may be obtained as

 −1 QPs0s0  = 0.05136 (7.29) cosϕ0i = costan 

The lower the power factor at ideal no-load, the lower the core loss in the machine (the winding losses are low in this case).

In general, when the machine is driven under load, the value of emf (E₁ = X_1mI_m) does not vary notably up to rated load and thus the core loss found from ideal no-load testing may be used for assessing performance during loading, through the loss segregation procedure. Note however that, on load, additional losses, produced by space field harmonics,occur. For a precise efficiency computation, these “stray load losses” have to be added to the core loss measured under ideal no-load or even for no-load motoring operation.

SHORT-CIRCUIT (ZERO SPEED) OPERATION

At start, the IM speed is zero (S = 1), but the electromagnetic torque is positive (Table 7.1), so when three-phase fed, the IM tends to start (rotate); to prevent this, the rotor has to be stalled.

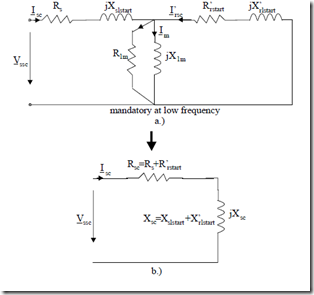
First, we adapt the equivalent circuit by letting S = 1 and R_r′ and X_sl, X_rl′ be replaced by their values as affected by skin effect and magnetic saturation

(mainly leakage saturation as shown in Chapter 6): X_slstart, R′_rstart, X′_rlstart (Figure 7.3).

 

Figure 7.3 Short-circuit (zero speed) operation:

a.) complete equivalent circuit at S = 1, b.) simplified equivalent circuit S = 1, c.) power balance, d.) phasor diagram, e.) three-phase zero speed testing, f.) single-phase supply zero speed testing

For standard frequencies of 50(60) Hz, and above, X_1m >> R′_rstart. Also, X_1m >> X′_rlstart, so it is acceptable to neglect it in the classical short-circuit equivalent circuit (Figure 7.3b).

For low frequencies, however, this is not so; that is, X_1m <> R′_rstart , so the complete equivalent circuit (Figure 7.3a) is mandatory.

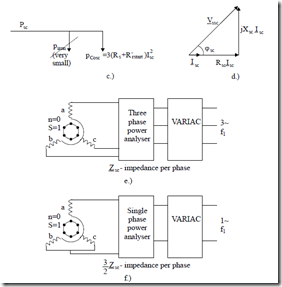
The power balance and the phasor diagram (for the simplified circuit of Figure 7.3b) are shown in Figure 7.3c and d. The test rigs for three-phase and single-phase supply testing are presented in Figure 7.3e and f.

It is evident that for single-phase supply, there is no starting torque as we have a non-traveling stator mmf aligned to phase a. Consequently, no rotor stalling is required.

The equivalent impedance is now (3/2)Z_sc because phase a is in series with phases b and c in parallel. The simplified equivalent circuit (Figure 7.3b) may be used consistently for supply frequencies above 50(60) Hz. For lower frequencies, the complete equivalent circuit has to be known. Still, the core loss may be neglected (R_1m ≈ ∞) but, from ideal no-load test at various voltages, we have to have L_1m(I_m) function. A rather cumbersome iterative (optimization) procedure is then required to find R′_rstart, X′_rlstart, and X_slstart with only two equations from measurements of R_sc, V_sc/I_sc.

Psc = 3R Is sc2 + 3R’rstart I’rsc2 (7.30)

Zsc = Rs + jXslstart + R’jXrlstart1m(R’+j Xrlstart( 1m++jX’X’rlstartrlstart)) (7.31)

This particular case, so typical with variable frequency IM supplies, will not be pursued further. For frequencies above 50(60) Hz the short-circuit impedance is simply

Zsc ≈ Rsc + jX ; Rsc sc = Rs + R’rlstart ; Xsc = Xslstart + X’rlstart (7.32) and with P_sc, V_ssc, I_sc measured, we may Rsc = 3PIsc_sc2 ; Xsc =(7.33)

for three phase zero speed testing and

Rsc = 23 IPsc~sc~2 ; Xsc = 23 (7.34)

for single phase zero speed testing.

If the test is done at rated voltage, the starting current I_start (I_sc)_Vsn is much larger than the rated current,

Istart ≈ 4.5 ÷8.0 In for cage rotors, larger for high efficiency motors, and

(7.35)

Istart ≈10 ÷12

(7.36)

In

for short-circuited rotor windings.

The starting torque T_es is:

Tes = 3R’rstartω1Istart p1 with	(7.37)
Tes = (0.7 ÷ 2.3)Ten for cage rotors and	(7.38)
Tes = (0.1÷0.3)Ten for short-circuited wound rotors.	(7.39)

 

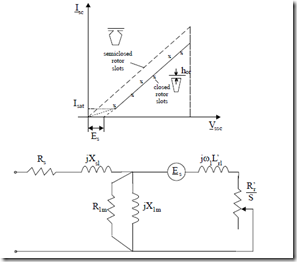
Figure 7.4 Stator voltage versus short-circuit current

Thorough testing of IM at zero speed generally completed up to rated current. Consequently, lower voltages are required, thus avoiding machine overheating. A quick test at rated voltage is done on prototypes or random IMs from, production line to measure the peak starting current and the starting torque. This is a must for heavy starting applications (nuclear power plant cooling pump-motors, for example) as both skin effect and leakage saturation notably modify the motor starting parameters: X_slstart, X′_rlstart, R′_rstart.

Also, closed slot rotors have their slot leakage flux path saturated at rotor currents notably less than rated current, so a low voltage test at zero speed should produce results as in Figure 7.4.

Intercepting the I_sc/V_sc curve with abscissa, we obtain, for the closed slot rotor, a non-zero emf E_s.[1] E_s is in the order of 6 to 12V for 220 V phase RMS, 50(60) Hz motors. This additional emf is sometimes introduced in the equivalent circuit together with a constant rotor leakage inductance to account for rotor slot−bridge saturation. E_s is 90⁰ ahead of rotor current I_r′ and is equal to

Es 2f 2W1 1 K ; Bsbridge hor Le (7.40)

B_sbridge is the saturation flux density in the rotor slot bridges (B_sbridge = (2 – 2.2)T). The bridge height is h_or = 0.3 to 1 mm depending on rotor peripheral speed. The smaller, the better.

A more complete investigation of combined skin and saturation effects on leakage inductances is to be found in Chapter 9 for both semiclosed and closed rotor slots.

Example 7.2 Parameters from zero speed testing

An induction motor with a cage semiclosed slot rotor has been tested at zero speed for V_ssc = 30 V (phase RMS, 60 Hz). The input power and phase current are: P_sc = 810 kW, I_sc = 30 A. The a.c. stator resistance R_s = 0.1Ω. The rotor resistance, without skin effect, is good for running conditions, R_r = 0.1Ω. Let us determine the short-circuit (and rotor) resistance and leakage reactance at zero speed, and the start-to-load rotor resistance ratio due to skin effect.

Solution

From (7.33) we may determine directly the values of short-circuit resistance and reactance, R_sc and X_sc,

Rsc = 3PI_scsc2 = 3810⋅302 = 0.3Ω;

 _{2 2} (7.41)

Xsc = ^ VI_scssc  − R_sc2 =  3030 − 0.3₂ = 0.954Ω

The rotor resistance at start R′rstart is
R’rstart = Rsc − Rs = 0.3− 0.1= 0.2Ω	(7.42)

So, the rotor resistance at start is two times that of full load conditions.

R’rstart = 0.2 = 2.0 (7.43)

R’_r 0.1

The skin effect is responsible for this increase.

Separating the two leakage reactances X_slstart and X′_rlstart from X_sc is hardly possible. In general, X_slstart is affected at start by leakage saturation, if the stator slots are not open, while X′_rlstart is affected by both leakage saturation and skin effect. However, at low voltage (at about rated current), the stator leakage and rotor leakage reactances are not affected by leakage saturation; only skin effect affects both R′_rstart and X′_rlstart. In this case it is common practice to consider

X X’_rlstart (7.44)

Incoming search terms:

• ideal no load test
• comment on an ideal no load speed In a d c motor
• comment on ideal no load speed