Proof of Nyquist Stability Criterion
This section is provided for those who are interested to understand the Nyquist stability criterion in depth. Those readers who are not interested to know the control theory in depth can skip this section and those readers who want to know the control theory in depth can refer to advanced control theory book such as the book “Mod- ern Control Engineering” published by Prentice-hall international, Inc. The book is two volumes and more than 1000 pages which is not suitable for engineers who want to know the basic control theory for real industrial applications. This section is extracted from the mentioned book and for industrial application the material given by next section is sufficient. This section has been added because it is interesting and is not too complicated and some modification has been made those material extracted from the above book to make it clearer.
Let F( s) be the ratio of two polynomial of function of s. The mapping theorem is used to prove the Nyquist stability criteria. The polynomials may have roots with the multiplicity of s = 0. Let the number of poles which can easily be found from the denominator be n and let the number of zeros which can easily be found from numerator be m. The zeros and poles lie in a closed contour which does not pass through any zeros or poles.
This closed contour is then mapped into F( s) plane as a closed curve, as repre- sentative point s traces out the entire contour in the s plane in the clockwise direc- tion. Let p = n − m be the difference between zeros and poles. The total number of p encirclement of the origin of F( s) plane clockwise direction, is p. Note that from this mapping only the difference of poles and zeros can be found. The proof of the mapping theorem is beyond the scope of this book.
Note that a positive p shows the excess of poles over zeros and negative p indicates an excess of zeros than poles. In control system with characteristic equation 1+ G(s) × H (s) the number of poles and zeros can easily be found from the characteristic function. G( s) is the forward path transfer function, which includes the control transfer function too and H( s) is the feedback transfer function. In this theorem the number of poles and zeros is immaterial only the number of encirclements of the origin is important.
Now the mapping theorem is used to prove the Nyquist stability criteria. For linear control system, let the closed contour in the s plane be all in the right portion of s plane with a semicircle with radios infinity which includes the entire imaginary axis. This is known as Nyquist path. The contour contains the complete iω axis from ω = − ∞ to ω = + ∞, where i is the complex operator. The direction of the path is clockwise. The Nyquist path encloses the entire left portion of the s plane. The Nyquist path also encloses all poles and zeros of the function of 1+ G(s) × H (s) that have positive real parts. It is necessary that the contour does not pass through any zeros and poles. If there are no zeros of the mentioned function in the right half of s plane, then there cannot be a closed loop pole in the right half of the s plane then the system is stable. If there is a pole or poles of G( s)H( s) in the origin the mapping is indeterminate and this is avoided by including a small detour around it.
If the mapping theorem is applied to the special case with F( s) = 1 + G( s)H( s), then we can make the following statement. Let the closed contour in the s plane cov- ering the complete right half of the s plane, then the number of half side of s plane zeros of the mentioned function is equal to the number of poles of the mentioned function in the right half plane plus the number of clockwise direction of encircle- ment of the origin of the closed loop function plane by corresponding closed curve in latter plane. Because of this assumed conditions then,
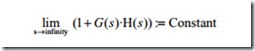The function (1 + G( s)H( s)) remains constant as s traverses the semicircle of infinite radius. Because of this, whether the locus of the above function encircle the origin of the function plane can be determined by considering only a part of the closed contour in the s plane, that is, the imaginary axes. Encirclement of the origin, if there are any, occur only while a representative point moves from iω to –iω along the imaginary axis, provided that no zeros or poles lie on the imaginary axis.
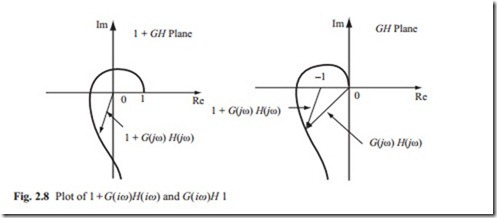
Note that the portion of 1 + G( s)H( s) contour from ω = −∞ to ω = ∞ is simply 1 + G( iω)H( iω). Since the 1 + G( iω)H( iω) is a vector sum of unit vector and the vector G( iω)H( iω), 1 + G( iω)H( iω) is identical to the vector drawn from the − 1 + 0i point to the terminal point of the vector G( iω)H( iω), as shown in Fig. 2.8. Usually j or i is used as complex operator. In Fig. 2.8 j is used as complex operator.
Encirclement of the origin by the graph of 1 + G( iω)H( iω) is identical to en- circlement of the − 1 + i0 point by just the G( iω)H( iω) locus. Thus, stability of a closed loop system can be investigated by examining encirclements of the − 1 + 0i point by the locus of G( iω)H( iω).
The number of clockwise encirclement of the − 1 point by the locus can be found by drawing a vector from the − 1 point to the GH locus starting from ω = −∞, going through ∞ = ∞ and by counting the number of clockwise rotation of the vector. Note that the locus of the function when ω goes from infinity to 0 is the mirror image of
the locus when ω goes from 0 to infinity about the real axis. In Fig. 2.18 the locus shows when ω travels from zero to infinity.
In the preceding discussion GH has been the ratio of two polynomials of s. Thus,
the transport lag e–Ts
has been excluded. Note, however, that a similar discussionapplies to systems with transport lag. The proof of this is beyond the scope of this book. The stability of a system with transport lag can be determined from the open loop frequency response curves by examining the number of encirclement 0 f −1 point, just as in the case of a system whose open loop transfer function is a ratio of two polynomials in s.
With the previous discussion now the Nyquist stability criterion can be estab- lished. For special case where there are no poles or zeros of the GH function on the imaginary axis, which is a special case, and if the GH transfer function has k poles
on the right half of the imaginary axis and lim
s→infinity
G(s)H (s) = constant, then the closed loop function as s travels from ω = − ∞ to ω = + ∞ is stable if the GH function
encircle the − 1 point k times. Note that when there are poles of the open loop trans- fer function in the right half of the imaginary axis, the open loop transfer function is unstable. The above stability criterion states that the closed loop transfer function becomes stable.
Now special cases of the system with various location of poles and zeros will be considered. The Nyquist stability criteria as described in the previous section can be defined as follows, Let n be number of zeros for the function 1 + G( s)H( s) and k the number clockwise encirclement of the − 1 point and let m be number of poles of G( s)H( s) in the right half of the s plane. Then the following statement can be made, n = k + m. If m is not zero for a stable control system the value of n must be zero, then k = −m, which means that there be m counter clockwise encirclement of the − 1 point. If G( s)H( s) does not have any poles in the right half of s plane then n = k. Thus, for stability there must be no encirclement of the − 1 point on the real axis. This is the proof of the Nyquist stability used in the next section.