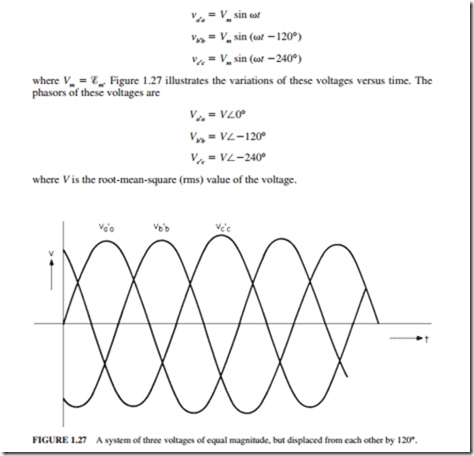
THREE-PHASE SYSTEMS
Most of the transmission, distribution, and energy conversion systems having an apparent power higher than 10 kVA use three-phase circuits. The reason for this is that the power density (the ratio of power to weight) of a device is higher when it is a three-phase rather than a single-phase design. For example, the weight of a three-phase motor is lower than the weight of a single-phase motor having the same rating. The voltages of a three-phase system are normally given by
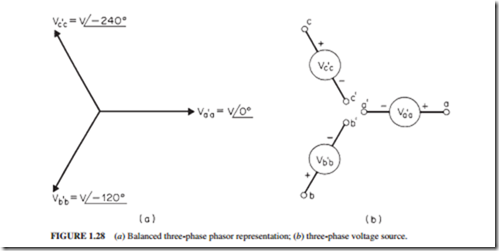
Figure 1.28a illustrates a graphical representation of the phasors. Figure 1.28b also shows the three voltage sources. When the three voltages are equal in magnitude, the system is called a three-phase balanced system. If the three voltages are unequal and/or the phase displacement is different from 120°, the system will be unbalanced. The phasor sum of the three voltages in a balanced system is zero.
Three-Phase Connections
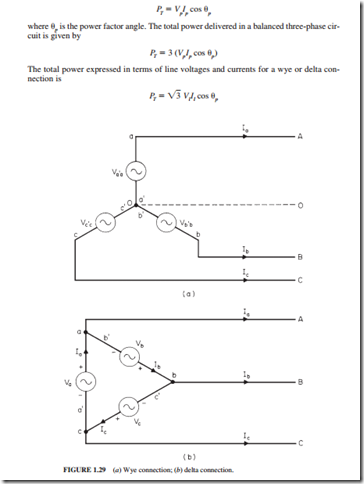
The three-phase voltage sources are normally interconnected as a “wye” (Y) and a “delta” (Ll), as shown in Figs. 1.29a and b, respectively. Terminals a¢, b¢, and c¢ join together in the wye connection to form the neutral point O. The system becomes a four-wire, three-phase system when a lead is brought out from point O. In the delta connection, terminals a and b¢, b and c¢, and c and a¢ are joined to form the delta connection.
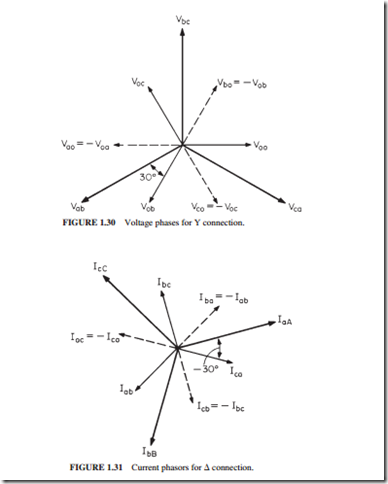
In the wye connection (Fig. 1.29a), the voltages across the individual phases are iden- tified as Va¢a, Vb¢b, and Vc¢c. These are known as phase voltages. The voltages across the lines a, b, and c (or A, B, and C ) are known as line voltages. The relationship between the line voltages and phase voltages is
Power in Three-Phase Systems
The average power in a single-phase ac circuit is given by
Figure 1.32 illustrates a graphical representation of the instantaneous power in a three- phase system. It is clear that the instantaneous power is constant and equal to 3 times the average power. This is an important feature for three-phase motors because the constant instantaneous power eliminates torque pulsations and resulting vibrations.