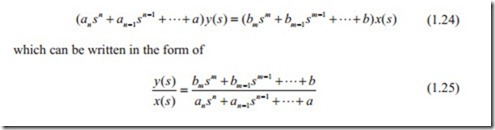Transfer Function
Taking Laplace Transform from both sides of Eq. (1.3) and assuming zero initial conditions yield
The right hand side of Eq. (1.25) is called the transfer function. am…, bm… are constants and y( s), x( s) are called the output and input variables. Equation (1.25) can be of any form but normally for real system n > m and n is called the order of transfer function.
The principle of superposition may be used for simple multivariable systems.
Once the transfer function is obtained, the following performance must be studied.
1. Stability
2. Transient response
3. Steady state error for various standard input
4. The above analysis should be carried out for various input functions
5. Frequency response
There are some standard transfer functions that can be solved and exact solution may be obtained. In the following, some standard transfer function is studied.
Related posts:
Alternators:Maximum Power Output
bipolar Transistors:Transistor substitution
Fixed Appliance and Socket Circuits:Testing Socket Circuits
ELECTRIC CONTROL FUNDAMENTALS:SERIES 90 CONTROL CIRCUITS
Objective tests on single-phase motors
Troubleshooting:Test Procedure Example 2
AUDIO AND VIDEO SYSTEMS - DISTORTION IN TAPE EQUIPMENT
Computations and circle diagrams:General , Circle Diagram for a Series Circuit and Circle Diagram fo...
Other Digital Audio Devices:High Definition Compatible Digital (HDCD)
Electrical Measurements—Meters:types of Meters
INDUSTRIAL INTELLIGENT CONTROLLERS:PLC (PROGRAMMABLE LOGIC CONTROL) CONTROLLERS
summary of current
Power and Energy:Energy
MICROPROCESSORS:MULTICORE MICROPROCESSOR UNITS