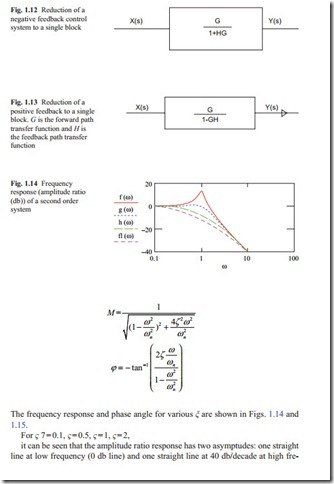
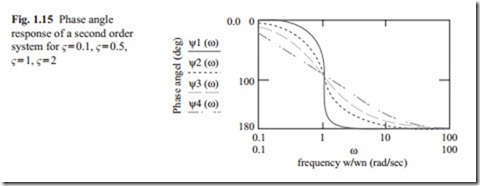
Frequency Response
For a second order system with transfer function,
the frequency response is obtained by replacing s with iω. After some algebraic manipulation, the amplitude ratio and phase angle are given by
quency. The phase angle changes from 0° to − 180° at high frequency. If ωn, ς are known, the frequency response can be calculated. If the experimental frequency response is obtained, then the natural frequency and damping ratio can be obtained from the result. Once natural frequency and damping ratio are known, the transfer function can be determined.
Conclusion
In this chapter, it was shown that by taking Laplace Transform from governing dif- ferential equations, the concept of transfer function can be introduced. Block dia- gram can then be used to represent the system. The standard first and second order transfer functions were studied. Negative and positive feedback was introduced. And some procedure was used to reduce the block diagram to a single block. In gen- eral, any system with any complexity can be reduced to a single block. The problem is then to study the stability, transient response, and steady state error.