A Numerical Investigation of the Transient Behavior of an Electrohydraulic Servo Motor Under Different Conditions
It has been shown by other research workers that the linearized model obtained in the previous sections provide a satisfactory model for the dynamic characteristic of electrohydraulic servo motors. In this section, the performance of a hydraulic axial piston motor type pm60, from Lucas Fluid Power is investigated. The specifications of the motor is as follows:
The maximum power rating of this motor is up to a maximum of 12 kW. The characteristic of the electrohydraulic servo valve is shown in Fig. 7.3, with a time constant of 0.0016 s. The performance of this motor with modified mathematical model of the DC motors is studied for different applications in both velocity and position control modes.
As discussed in the chapter of DC servo motors, various control strategies may be considered. It also depends on the performance requirements. For very high performance applications, the flexibility of the transmission shaft must also be considered. The optimized performance using compensation techniques such as acceleration feedback and lead-lag network in additions to the proportional and integral control techniques must be studied. The use of acceleration feedback must be avoided because mechanical signals contain a lot of noise. If acceleration feedback has to be used, the velocity, which easily is obtainable from a high performance tacho must be differentiated. In this case, a low pass filter must also be added to the acceleration signal. For complex system, that is, system of higher order than three, the state variable feedback as discussed in previous chapters must be considered.
In this example a fifth-order transfer function is considered and a proportional and integral control and a lead-lag network are used to move the dominant roots of the characteristic to desired position on the s plane. The other roots which are not dominant in the response must be stable with a little damping. This damping makes sure that high frequency signals to disappear in the response of the system.
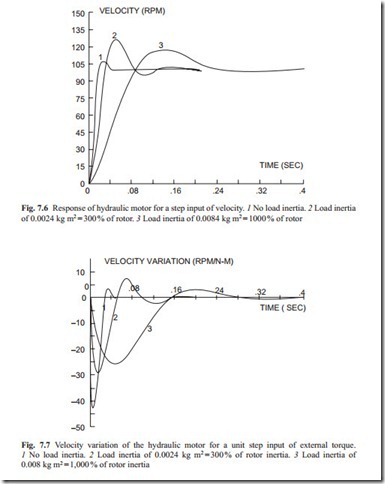
Large inertia in servo motors causes a lot of problems. This effect in the hydraulic motor was studied and the results are presented in Fig. 7.6 for velocity control case. For each load inertia the parameters of the controller must be adjusted to obtain satisfactory response characteristics. The load inertia is presented as a percentage of rotor inertia to make sure that there is reference inertia (rotor inertia) to compare with the load inertia.
The effect of a unit step input of external torque for various load inertia is presented in Fig. 7.7. It can be seen that the velocity drop for large load inertia is smaller than the case when the load inertia is smaller. Because of the integral term in the controller, the steady state error is zero.
It should be noted that the response as presented in Fig. 7.5 is only valid for small variation of velocity. At large step input, the motor produces maximum torque and the inertia accelerates up to the vicinity of the final velocity in which case it settles down according to the dynamic model of the system. In the above example, the flexibility of the transmission mechanism was very small and that is the reason that the higher frequency of oscillations does not show themselves in the response.
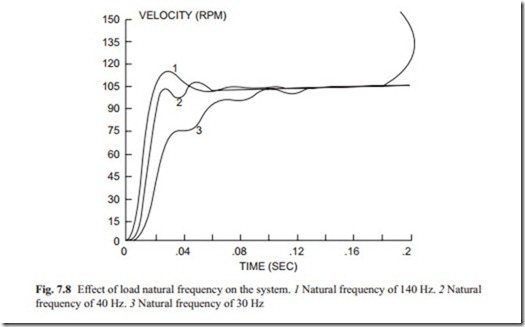
A typical step input response for various natural frequencies of the transmission mechanism is shown Fig. 7.8.
It can be seen as the natural frequency of the transmission mechanism reduces, its response characteristic becomes more dominant in the step input response. In Fig. 7.8, it is obvious that there are two pairs of complex roots and that there is A Numerical Investigation of the Transient Behavior
one negative root. This shows that the characteristic equation is in order of five. Of course for every change, the parameters must be changed to obtain satisfactory response to a change of input signal. The satisfactory conditions must be defined first and then try to adjust the parameters of the controller to meet those requirements.
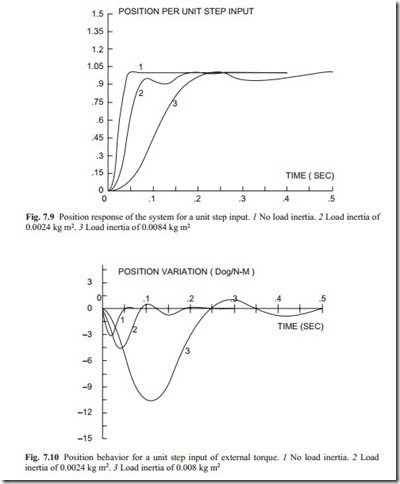
It is always a good idea to study servo motors in velocity controlled closed loop. For closed loop control, the velocity closed loop system should have a slight over- shoot. Then the loop must be closed for position control with a proportional controller. With this method, the gain of the controller should be adjusted to obtain a satisfactory position control performance. A typical step input response is shown in Fig. 7.9.
The effect of step input of external torque is shown in Fig. 7.10.
The important properties to notice is that the response is much slower than the velocity closed loop. The reason is that position is the integral of velocity which is inherently slower. The second property is that the dynamic velocity drop is larger when the load inertia is increased. The steady state error is zero because there is an integrator in the system. For a better position control, that is, faster response and smaller position error, the acceleration feedback may be introduced. There is no acceleration transducer and the velocity signal must be differentiated to provide feedback. In this case, a low pass first-order or second-order filter must be used. The filter does not filter low signal noise in which case acceleration feedback cannot be used. The reader is encouraged to derive the mathematical transfer function and to study the performance.
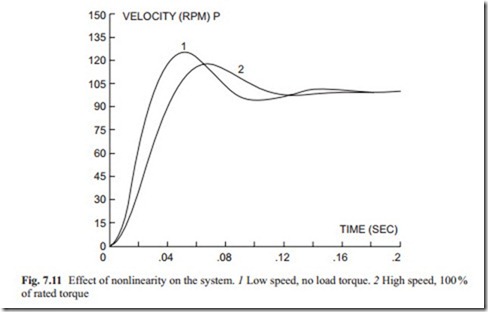
As mentioned above, the servo valve is inherently nonlinear and a linearized model was obtained. The effect of nonlinearity can be investigated considering two
extreme positions, first when there is no external torque and the motor operates at very low velocity. In this case, the spool valve operates in the vicinity of closed position. Secondly, when the motor runs at maximum speed maximum torque is applied to the motor. The second case represents the case when the spool valve is fully opened. This is shown in Fig. 7.11. It shows that the linearized model can be used for complete range of operation. It is usually a good idea to study the performance over whole range of operation.
There is other nonlinearity that cannot be modeled by a linear model. The static friction in the spool valve is a typical case. This nonlinearity affects the system considerably. Usually the manufacturers of valves provide a high frequency signal which oscillates the spool valve with very small amplitude. This reduces the static friction considerably.
Conclusion
In this chapter, first the behavior of spool valve, a jack, and a mechanical linkage for position control applications was investigated. By ignoring the compressibility of oil, a second-order transfer function was obtained. The behavior can completely be described by natural frequency and a damping ratio. The reader is encouraged to study the system by including the compressibility of oil in which the system will be third order. The performance can be predicted by calculating the roots of characteristic equation and the gain can be changed to obtain an optimum response.
The electrohydraulic servo motor was then studied. The flow equation, torque equation, and the dynamic behavior of servo motor were introduced. The complexity of the model would depend on what is important in the model. For very high performance, the flexibility of the transmission shaft must be also considered. It is better to include the transmission flexibility in the mathematical model and control it instead of designing a very stiff system which makes the system very heavy which in turn requires a larger motor.