Periodic and Aperiodic Signals
Sounds can be divided into these two categories and analyzed either in the time domain in which the waveform is considered or in the frequency domain in which the spectrum is considered. The time and frequency domains are linked by transforms of which the best known is the Fourier transform.
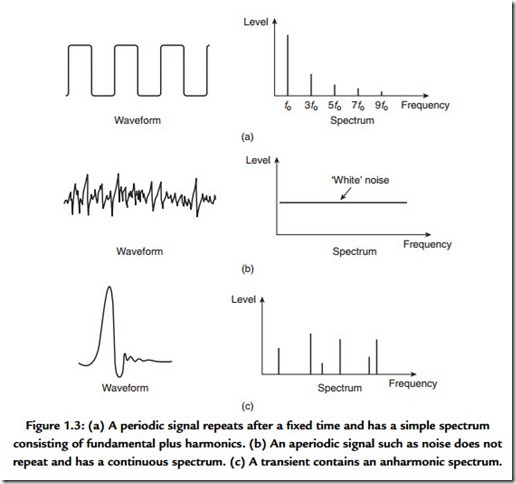
Figure 1.3(a) shows that an ideal periodic signal is one which repeats after some constant time has elapsed and goes on indefinitely in the time domain. In the frequency domain such a signal will be described as having a fundamental frequency and a series of harmonics or partials that are at integer multiples of the fundamental. The timbre of an instrument is determined by the harmonic structure. Where there are no harmonics at all, the simplest possible signal results that has only a single frequency in the spectrum. In the time domain this will be an endless sine wave.
Figure 1.3(b) shows an aperiodic signal known as white noise. The spectrum shows that there is an equal level at all frequencies, hence the term “white,” which is analogous to the white light containing all wavelengths. Transients or impulses may also be aperiodic. A spectral analysis of a transient [Figure 1.3(c)] will contain a range of frequencies, but these are not harmonics because they are not integer multiples of the lowest frequency. Generally the narrower an event in the time domain, the broader it will be in the frequency domain and vice versa.